 |
методом эквивалентного генератора
|
|
|
|
Метод эквивалентного генератора относится к классу методов, основанных на принципе упрощения электрической схемы цепи – когда с помощью тех или иных методов преобразования сложная схема электрической цепи упрощается до простой электрической схемы, в которой можно найти искомый ток по закону Ома. Сущность метода эквивалентного генератора состоит в следующем: любая, сколь угодно сложная схема линейной электрической цепи, может быть представлена относительно двух своих узлов в виде простой цепи – последовательного соединения источника ЭДС с внутренним сопротивлением (активного двухполюсника) и сопротивления нагрузки; ток в такой цепи легко найти по закону Ома.
На рис. 2.8 представлена эквивалентная электрическая схема так называемого эквивалентного генератора. Она содержит эквивалентный генератор, состоящий из ЭДС эквивалентного генератора 
с внутренним сопротивлением 
(левая часть схемы рис. 2.8, выделенная штриховой линией) и нагрузку этого генератора 
.
Если к такой эквивалентной схеме привести анализируемую цепь рис. 2.7, то затем найти ток 
в этой цепи можно будет по закону Ома:
. (2.54)
Рис. 2.8. Электрическая схема эквивалентного генератора.
Для рассмотрения метода эквивалентного генератора используем первоначальную анализируемую схему рис. 2.1 в виде, показанном ранее на рис. 2.5, где источники тока 
и 
первоначальной схемы рис. 2.1 преобразованы в эквивалентные им источники ЭДС 
и 
на схеме рис. 2.5. Исключив в схеме рис. 2.5 обозначения направлений обхода контуров цепи, получим схему, показанную на рис. 2.9.
Рис. 2.9. Эквивалентная схема анализируемой электрической цепи
В качестве искомого тока примем ток 
. После этого схему рис. 2.9 перерисуем и представим в виде, показанном на рис. 2.10.
|
|
|
На этом рисунке дополнительно введена точка 
, а анализируемая схема представлена так, чтобы было удобно рассматривать её относительно точек 
. Тогда эквивалентный генератор (левая относительно этих точек часть схемы) и его нагрузка (правая относительно этих точек часть схемы) будут соответствовать расположению этих элементов, принятых на рис. 2.8.
Рис. 2.10. Схема анализируемой цепи с сопротивлением 
, выделенным в качестве нагрузки эквивалентного генератора (искомый ток 
)
Для того, чтобы воспользоваться выражением (2.54) закона Ома для цепи, содержащей эквивалентный генератор и его нагрузку, необходимо привести левую относительно точек часть схемы сложной анализируемой цепи рис. 2.10 к виду, показанному на рис. 2.8 для эквивалентного генератора. Роль нагрузки схемы рис. 2.8 будет выполнять сопротивление 
схемы рис. 2.10.
Для преобразования схемы рис. 2.10 в схему рис. 2.8, следует определить ЭДС эквивалентного генератора и его внутреннее сопротивление .
Для определения ЭДС эквивалентного генератора , удалим сопротивление в схеме рис. 2.10, получившуюся схему покажем на рис. 2.11, а, а затем заменим её эквивалентной схемой рис. 2.11, б.
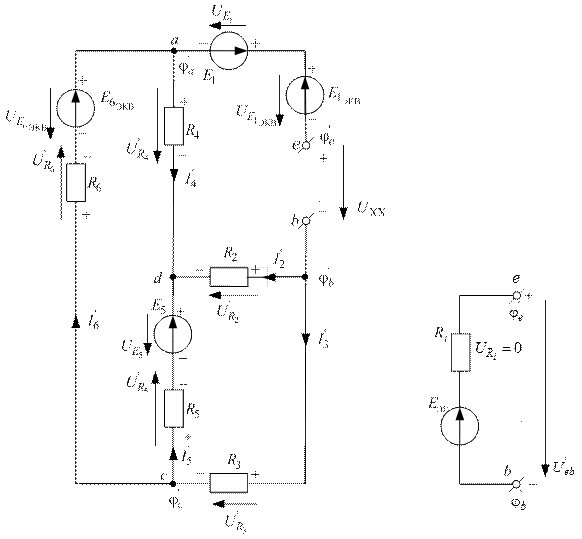а б
Рис. 2.11. Схема анализируемой цепи в режиме холостого хода (а));
эквивалентная схема анализируемой цепи в виде схемы
эквивалентного генератора (б))
После таких преобразований, когда анализируемая цепь рис. 2.10 переведена в режим холостого хода относительно точек (рис. 2.11, а), естественно, режим её работы изменится: изменятся токи ветвей и падения напряжений на сопротивлениях. Это изменение режима работы цепи отражено на рис. 2.11, а тем, что все обозначения токов ветвей и падений напряжений на сопротивлениях имеют верхний индекс «штрих».
Установление режима холостого хода относительно точек приводит к тому, что ток во внешней цепи генератора, эквивалентного анализируемой цепи (рис. 2.11, б), равен нулю, падения напряжения 
на внутреннем сопротивлении генератора и все напряжение эквивалентного генератора оказывается приложенным к точкам 
и этой цепи. Таким образом, ЭДС эквивалентного генератора равно напряжению холостого хода анализируемой схемы относительно разомкнутых клемм схемы. То есть, условие обеспечения холостого хода в первой ветви рис. 2.10, ток которой следует определить, выглядит так:
|
|
|
, (2.55)
. (2.56)
Тогда можно найти ЭДС эквивалентного генератора , показанного на рис. 2.11, б, которое оказывается равным напряжению холостого хода 
(рис. 2.11, а):
, (2.57)
оно же оказывается равным напряжению 
(рис. 2.11 б):
, (2.58)
а падение напряжения на внутреннем сопротивлении эквивалентного генератора рис. 2.11, б при этом равно нулю:
. (2.59)
Выражение (2.58) показывает, каким образом можно определить напряжение холостого хода и эквивалентного генератора – они равны разности потенциалов 
между точками и схемы анализируемой цепи при холостом ходе в ветви определяемого тока. При этом остается определить указанные потенциалы любым известным методом расчета сложных электрических цепей.
Второй неизвестной величиной в выражении (2.54) является внутреннее сопротивление эквивалентного генератора. Для его определения необходимо найти входное сопротивление схемы рис. 2.11, а, которое и будет этим сопротивлением . При этом наличие источников ЭДС и источников тока не имеет значения для сопротивления схемы, так как их внутренние сопротивления равны, соответственно, либо нулю, либо бесконечности. Учитывая, что внутреннее сопротивление источников ЭДС нулевое и на величины сопротивлений ветвей не влияет, преобразуем схему рис. 2.11, а, содержащую источники ЭДС, в схему рис. 2.12, содержащую только сопротивления без источников.
Рис. 2.12. Схема анализируемой цепи без источников ЭДС для определения внутреннего сопротивления эквивалентного генератора
Анализ схемы рис. 2.12 показывает, что в представленном виде эта схема не содержит последовательных и параллельных соединений. Соединения сопротивлений в этой схеме представляют собой звезды и треугольники:
|
|
|
- сопротивления 
, 
, 
, соединенные между собой в узле 
, соединены звездой;
- сопротивления , 
, 
, соединенные между собой в узле 
, также соединены звездой;
- сопротивления , , , соединены между собой треугольником;
- сопротивления , , , соединены между собой также треугольником.
Для преобразования сложной электрической цепи, схема которой содержит соединения сопротивлений треугольниками и звездами, проще всего преобразовать один из треугольников сопротивлений в эквивалентную ему звезду.
Для схемы рис. 2.12 преобразуем, например, треугольник сопротивлений , , в эквивалентную ему звезду. Это преобразование иллюстрируется рис. 2.13, a,b.
В соответствии с правилом преобразования треугольника сопротивлений , , 2.13, a, в эквивалентную ему звезду 
, 
, 
2.13, б, запишем сопротивления лучей звезды , , 2.13, б через сопротивления сторон треугольника , , 2.13, a:
, (2.60)
, (2.61)
. (2.62)
Образовавшийся при этом дополнительный узел 
является промежуточным и во всех последующих преобразованиях не участвует.
а б
Рис. 2.13. Преобразование треугольника сопротивлений 
(а) в
эквивалентную звезду 
(б)
После определения сопротивлений , , лучей звезды рис. 2.13, б, эквивалентной исходному треугольнику рис. 2.13, а сопротивлений , , , можно будет найти входное сопротивление схемы рис. 2.12 относительно точек 
. Это сопротивление и будет внутреннее сопротивление эквивалентного генератора схем рис. 2.8, рис. 2.11, б. Для этого схему рис. 2.12 необходимо перерисовать с учетом замены треугольника сопротивлений , , рис. 2.13, а на эквивалентную ему звезду сопротивлений , , , рис. 2.13, б. Такая схема показана на рис. 2.14. После преобразования треугольника сопротивлений , , на эквивалентную ему звезду сопротивлений , , , сопротивления и оказываются включенными последовательно, и их общее сопротивление 
равно:
. (2.63)
Рис. 2.14. Эквивалентная схема анализируемой цепи для определения внутреннего сопротивления эквивалентного генератора 
|
|
|
Сопротивления и также оказываются включенными последовательно между собой и их общее сопротивление 
равно их сумме:
. (2.64)
Полученные в выражениях (2.63) и (2.64) сопротивления и оказываются включенными между собой параллельно. Их общее сопротивление 
(относительно узлов 
и a) равно:
. (2.65)
Сопротивление оказывается включенным последовательно с сопротивлением (схема рис. 2.14). Их общее сопротивление 
относительно точек схемы рис. 2.14, рис. 2.12, рис. 2.11, а, оказывается равным внутреннему сопротивлению эквивалентного генератора рис. 2.11, б и рис. 2.8:
. (2.66)
После определения величины ЭДС эквивалентного генератора (2.58) и его внутреннего сопротивления (2.66), можно найти величину искомого тока из выражения (2.54):
. (2.67)
В описанном нами методе эквивалентного генератора внутреннее сопротивление эквивалентного генератора было получено путем преобразования исходной анализируемой схемы рис. 2.9 к виду рис. 2.11, б путем упрощения исходной схемы (2.60) – (2.66). Однако, существует другой способ расчета внутреннего сопротивления эквивалентного генератора – через использование параметров режимов холостого хода (ХХ) и короткого замыкания (КЗ) на выходе цепи (относительно точек схемы, для которых определяется её сопротивление). Мы не будем подробно рассматривать этот способ определения величины , запишем только выражение для определения этого сопротивления через ток короткого замыкания 
и напряжение холостого хода :
, (2.68)
где режимы холостого хода и короткого замыкания определяются относительно точек схемы рис. 2.14.
Таким образом, найти входное сопротивление некоторой схемы относительно двух заданных точек схемы можно двумя основными путями: преобразованием сложной схемы в простую, или взяв отношение напряжения холостого хода к току короткого замыкания относительно заданных точек схемы.
Порядок расчета сложной электрической цепи методом эквивалентного генератора таков:
- сопротивление 
, включенное между двумя точками сложной электрической цепи, в котором необходимо найти ток 
, представляют нагрузкой и отключают от остальной части цепи, создав таким образом относительно этих точек цепи режим холостого хода с напряжением между ними;
- остальную часть сложной цепи представляют активным двухполюсником с некоторой ЭДС и внутренним сопротивлением , последовательное включение которых представляет собой эквивалентный генератор;
- любым известным способом рассчитывают величину ЭДС эквивалентного генератора как напряжение холостого хода относительно точек схемы, от которых отключено сопротивление с искомым током;
|
|
|
- величину внутреннего сопротивления генератора определяют либо как входное сопротивление схемы относительно точек цепи, от которых отключено сопротивление с искомым током, либо как отношение напряжения холостого хода к току короткого замыкания на этом же участке цепи;
- искомый ток находят как частное от ЭДС эквивалентного генератора на величину суммы внутреннего сопротивления эквивалентного генератора и сопротивления ветви с искомым током.
2.5. Баланс мощностей в электрической цепи постоянного тока
Баланс мощностей в электрической цепи означает, что мощность, которую выделяют все источники энергии, равна мощности, которую потребляют в этой же цепи все приемники энергии:
, (2.69)
где 
– мощность i- го источника ЭДС или тока, Вт; 
– мощность, выделяемая в j- м сопротивлении, Вт.
Очевидно, что баланс мощностей следует из закона сохранения энергии.
Запишем для анализируемой цепи рис. 2.15 сумму мощностей, выделяемых всеми источниками энергии. При этом мощности, выделяемые источниками ЭДС и тока, будем считать положительными, если ток в ветви, где установлен источник ЭДС или тока, совпадает с направлением тока внутри источника (со стрелкой в обозначении источника ЭДС или тока), и отрицательными, если направление тока в ветви противоположно направлению тока в источнике. Тогда, составив соответствующее уравнение для вычисления суммарной мощности, отдаваемой источниками ЭДС и тока в анализируемую цепь и подставив в него численные значения, получим суммарную мощность источников:
[Вт]. (2.70)
при этом токи ветвей должны подставляться в уравнение (2.70) со своим знаком, который получился при их расчете.
Суммарная мощность, рассеиваемая в цепи сопротивлениями (приемниками энергии), для той же цепи рис. 2.15, может быть найдена так:
[Вт]. (2.71)
В результате расчета (2.70) – выделяемая источниками мощность, и (2.71) – потребляемая сопротивлениями мощность в цепи – должны быть одинаковы.
2.6 Потенциальная диаграмма электрической цепи
постоянного тока
Потенциальная диаграмма контура электрической цепи постоянного тока – это графическое изображение второго закона Кирхгофа, в котором вместо падений напряжений записаны потенциалы узлов электрической цепи. Она показывает суммарное значение потенциала и суммарное сопротивление в данной точке цепи того контура, для которого построена диаграмма, считая от опорного узла, потенциал которого принят за нулевой. Иными словами, потенциальная диаграмма показывает распределение потенциалов и сопротивлений в том контуре цепи, для которого она построена.
Графически эта диаграмма представляет собой ломаную линию, изображенную в декартовой системе координат, горизонтальной осью которой (осью абсцисс) является ось сопротивлений , а вертикальной осью (осью ординат) – ось потенциалов 
.
Процесс построения потенциальной диаграммы электрической цепи рассмотрим для той же, что и ранее, электрической цепи, показанной на рис. 2.3, и модифицированной для удобства построения потенциальной диаграммы так, как показано на рис. 2.15.
Поскольку для построения потенциальной диаграммы требуется знание численных значений токов ветвей и сопротивлений ветвей, приведем эти численные значения для цепи рис. 2.15 при условии, что исходные данные для расчета этой цепи таковы: 
Ом, 
Ом, 
Ом, 
Ом, 
Ом, 
Ом; величины источников ЭДС: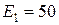 
В, 
В; величины источников тока: 
А, 
А. Значения токов 
в ветвях цепи, рассчитанные прямым применением законов Кирхгофа (сам расчет здесь не приводится), таковы: 
[А]; 
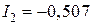[А]; 
[А]; 
[А]; 
[А]; 
[А].
Построение потенциальной диаграммы начнем с выбора контура, для которого эта диаграмма будет составляться. На наш взгляд, наиболее информативно будет построить потенциальную диаграмму для контура d-b-m-a-c-s-d, так как в этом контуре содержатся все источники ЭДС и источники тока анализируемой цепи и при таком обходе на потенциальной диаграмме будут показаны потенциалы всех узлов анализируемой схемы. Далее произведем выбор опорного узла, потенциал которого примем за ноль. Есть смысл взять за опорный узел d, как и ранее при расчетах анализируемой цепи. Потенциал этого узла положим равным нулю, как и ранее (2.44).
Определим численные значения потенциалов узлов и точек анализируемой схемы, находящихся на пути обхода выбранного нами контура d-b-m-a-c-s-d. Поскольку потенциал узла d равен нулю (2.44), то потенциал 
узла b определится так:
[В]. (2.72)
Знак «плюс» при произведении 
означает, что потенциал узла b повышается при переходе от узла d анализируемой схемы к узлу b (см. полярность падения напряжения на сопротивлении 
от тока 
на схеме рис. 2.15).
Следующим определим потенциал 
точки m анализируемой схемы:
[В]. (2.73)
Знаки при произведениях 
и 
соответствуют полярностям, показанным на схеме рис. 2.15.
Следующим за точкой m анализируемой схемы идет узел a. Его потенциал 
равен:
[В]. (2.74)
Рис. 2.15. Эквивалентная схема анализируемой электрической цепи для построения потенциальной диаграммы
Далее определим потенциал 
узла c, значение которого составит:
[В]. (2.75)
Потенциал 
точки s, следующей за узлом c по выбранному нами обходу, равен:
[В]. (2.76)
Обойдя таким образом весь контур d-b-m-a-c-s-d, мы возвращаемся в узел d. При этом потенциал 
узла d должен стать равным нулю. В самом деле, так оно и происходит, так как при подходе из узла c к узлу d, потенциал последнего станет равен:
[В]. (2.77)
После расчета численных значений потенциалов для контура d-b-m-a-c-s-d можно построить саму потенциальную диаграмму. Эта диаграмма показана на рис. 2.16.
Техника построения потенциальной диаграммы такова. На осях декартовой системы координат откладывают значения потенциалов и сопротивлений для контура цепи (схемы), который был ранее выбран для построения потенциальной диаграммы. В нашем примере, рис. 2.15, это контур d-b-m-a-c-s-d. Значения заранее рассчитанных величин потенциалов для каждой из точек этого контура откладывают на вертикальной оси (оси ординат) в положительную или отрицательную область значений, в зависимости от знака потенциала, полученного ранее при расчете. В нашем примере это будут потенциалы , , , , , и вновь точек d-b-m-a-c-s-d, соответственно. Порядок следования значений потенциалов в потенциальной диаграмме соответствует их порядку при расчете значений потенциалов. В анализируемой нами цепи рис. 2.15, этот порядок , , , , , , соответствует обходу контура d-b-m-a-c-s-d. Значения сопротивлений откладываются по горизонтальной оси (оси абсцисс) декартовой системы координат. За нулевое (исходное) значение сопротивления в потенциальной диаграмме принимается значение в опорном узле; в нашем примере рис. 2.15 это значение сопротивления в узле d. Далее, по мере обхода контура цепи, который выбран для построения потенциальной диаграммы (в нашем примере это контур d-b-m-a-c-s-d), значения сопротивлений в каждой последующей точке прибавляются к значениям сопротивлений в предыдущей точке.
Таким образом, сопротивление в каждой точке потенциальной диаграммы контура оказывается суммарным для этой точки, начиная с опорного узла, где значение сопротивления принято за ноль. Если при переходе из одной точки контура в другую сопротивления в схеме цепи нет, то к предыдущему значению сопротивления прибавляется ноль (это имеет место при прохождении источника ЭДС с нулевым внутренним сопротивлением).
Рис. 2.8.2 Потенциальная диаграмма контура d-b-m-a-c-s-d исследуемой цепи
В нашем примере значения сопротивлений в точках потенциальной диаграммы контура d-b-m-a-c-s-d составят:
[Ом]. (2.78)
Таким образом, при построении потенциальной диаграммы контура электрической цепи по вертикальной оси декартовой системы координат откладывают потенциалы узлов по мере их упоминания при обходе контура, а по горизонтальной оси – нарастающим итогом сопротивления также по мере их упоминания при таком обходе. Используют потенциальную диаграмму цепи для наглядного визуального представления распределения потенциалов и соответствующих им сопротивлений по тому или иному контуру электрической цепи.
Библиографический список
1. Основы теории цепей. Методические указания и контрольные задания для студентов радиотехнического факультета спец. 0701 “Радиотехника”.-Сост. Ю.А.Мантейфельд, А.Д.Суслов. М.: МИРЭА.-1980.-48 с.
2. Основы теории цепей. Методические указания по выполнению расчетно-графических заданий №1-2 для студентов радиотехнического факультета. Сост. В.И.Вепринцев. Красноярск: Изд-во КГТУ, 2000. 64 с.
3. Шебес, М.Р., Каблукова, М.В. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич. Спец. вузов.-4-е изд. перераб. и доп.-М.: Высш. шк., 1990.-544 с.: ил.
4. Основы теории цепей: учебник для вузов / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
5. Теория линейных электрических цепей: учебник для вузов / Б.П.Афанасьев, О.Е.Гольдин, И.Г.Кляцкин, Г.Я.Пинес. – М.: Высш. шк., 1973. – 592 с.
Оглавление
1. ЗАДАНИЕ И ВЫБОР ВАРИАНТА ДЛЯ ЕГО ВЫПОЛНЕНИЯ.. 4
2. РАСЧЕТ ВЕЛИЧИН ТОКОВ НЕПОСРЕДСТВЕННЫМ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА, МЕТОДАМИ КОНТУРНЫХ ТОКОВ, УЗЛОВЫХ ПОТЕНЦИАЛОВ И МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА.. 9
2.2. Анализ (расчет) сложных электрических цепей. 19
методом контурных токов. 19
2.6.3 Анализ (расчет) сложных электрических цепей. 25
методом узловых потенциалов. 25
2.6.4 Анализ (расчет) сложных электрических цепей. 31
методом эквивалентного генератора. 31
2.5. Баланс мощностей в электрической цепи постоянного тока. 40
2.6 Потенциальная диаграмма электрической цепи. 41
постоянного тока. 41
Библиографический список. 47
Оглавление. 48
|
|
|
