 |
Оптимизация модели энергосистемы методом множителей Лагранжа. Основные выражения.
|
|
|
|
Порядок построения расчетной модели ТЭС. Основные выражения.
В рассмотренной методике до формулы (1) вставляются характерис-тики работающих турбин:
Gпараi = Spl_6(Wi, Qi),
где Gпара =Σ Gпараi
при условии: WТЭЦ =Σ Wi
QТЭЦ =Σ Qi
А сама формула (1) «переворачивается» и дополняется формулой (2):
(9)
Получаем ожидаемую (прогнозируемую) величину сожженного топлива.
Потери электроэнергии на привод питательных, циркуляционных, теплофикационных насосов и вентиляционных установок тяги и дутья (основных потребителей электроэнергии на ТЭС) вычисляем также по нормативным характеристикам, представленным в модели в виде кубических сплайнов.
Порядок построения и оптимизации насосной станции. Основные выражения.
Обычно любая насосная станция представляет собой несколько центро-бежных (или диагональных) насосов, работающих на общий коллектор.
Расход воды из коллектора регулируется дроссельными клапанами потребителей. Сами насосы регуляторов расхода не имеют.
Поэтому будет справедлива система n+1 уравнений, содержащая n+1 неизвестных - Q1, Q2, …, Qn, Н:
H = Spl_4(Q1),
H = Spl_4(Q2),
… (10)
H = Spl_4(Qn),
Q = Σ Qn
После решения этой системы уравнений определяется величина требуемой электрической мощности насосной станции:
W1 = Spl_4(Q1),
W2 = Spl_4(Q2),
… (11)
Wn = Spl_4(Qn),
W = Σ Wn.
Согласно такой схеме включения для некоторых насосов расход Q может быть предельным (нулевым или даже отрицательным).
Оптимизация модели энергосистемы методом множителей Лагранжа. Основные выражения.
Оптимизация параметров работы тепловых электростанций (ТЭС) и энергосистемы (ЭС) в целом позволяют обеспечить существенную экономию топлива практически без дополнительных капитальных вложений, что является весьма актуальным.
|
|
|
Для каждой ТЭС имеется своя зависимость расхода топлива от выраба-тываемой активной мощности Bi = f(Pген,i), которая называется расходной характеристикой ТЭС.
В качестве топлива для ТЭС может использоваться уголь, газ, щепа и другие виды органического топлива, поэтому при определении расходной характеристики ТЭС в энергетике РБ и РФ используется понятие «условного топлива», равного по теплотворной способности 1 килограмму каменного угля или 29,3 МДж (7000 Ккал).
Если бы расходные характеристики были линейны и одинаковы для всех станций, то суммарный расход условного топлива не зависел бы от распределения активных мощностей между ТЭС. В действительности эти характеристики нелинейны и различны. Поэтому изменение распределения генерируемых активных мощностей между ТЭС в энергосистеме приводит и к изменению расхода условного топлива.
Существует оптимальное распределение активных мощностей, соответствующее минимуму расхода условного топлива при выработке заданной активной мощности.
При оптимизации режимов электроэнергетических систем наибольшее распространение получили метод множителей Лагранжа и градиентные методы.
Также используется метод динамического программирования (метод Беллмана), метод эквивалентирования групп ТЭС с условно одинаковыми расходными характеристиками, и некоторые другие. В настоящее время разрабатываются также альтернативные алгоритмы оптимизации режимов, в частности, с использованием методов нечеткой логики и эволюционных алгоритмов.
Эти методы основаны на предположении, что расходные характеристики ТЭС имеют определенные аналитические выражения и минимальное количество ограничений, что вполне приемлемо, например, для ТЭС с конденсационными турбинами.
В качестве критерия оптимизации выберем расход условного топлива на выработку электроэнергии в энергосистеме регионального уровня, например, уровня Витебскэнерго.
|
|
|
Соответствующая целевая функция оптимизации имеет вид:
 , (12)
, (12)
где Вi – расход условного топлива на i–й ТЭС на выработку активной электрической мощности,
под (m +1)-й ТЭС понимается балансирующий узел энергосистемы, расходная характеристика которого известна.
В энергосистеме РУП Витебскэнерго и Белорусской энергосистеме в целом таким балансирующим узлом является Лукомльская ГРЭС, имеющая эквивалентную характеристику замещающей конденсационной электростанции 0,320 кг/кВтч.
Баланс активных мощностей в энергосистеме можно записать:
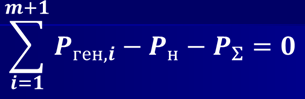 13
13
где Pген,i – активная мощность, генерируемая i -й ТЭС в энергосистему;
Pн – активная нагрузка в электросети;
P Σ – суммарные потери активной мощности в сети.
Уравнение оптимизации в виде функции Лагранжа будет иметь вид:
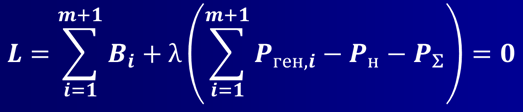 14
14
Активная мощность нагрузок считается постоянной величиной, а потери – функцией генерируемых мощностей, за исключением мощности балансирую-щего узла.
Так как выражение для баланса мощности равно нулю (13), то минимумы функции Лагранжа (14) будут совпадать с минимумами целевой функции (12).
Для поиска глобального оптимума продифференцируем функцию Лагранжа по переменным Рген,i и приравняем производные нулю.
Получим систему уравнений:

|
|
|


