 |
Дифференциальные уравнения
|
|
|
|
1. Постановка задачи. Понятие дифференциального уравнения. Основные определения. Уравнения первого порядка (общие понятия) [ 3, гл. XIII, §1].
2. Уравнения с разделяющимися переменными. Однородные уравнения. Линейные уравнения первого порядка. Уравнение Бернулли [ 3, гл. XШ, §§4,5,7,8].
3. Способы понижения порядка дифференциального уравнения [ 3, гл. XIII, §§ 17,18, 2 гл. IV, §2, п. 2-4].
4. Линейные уравнения второго порядка. Общие свойства [ 3, гл. XIII, §§ 20, 23].
5. Линейные уравнения второго порядка с постоянными коэффициентами. Общее решение однородного уравнения. Частное решение не однородного уравнения с правой частью специального вида. Метод вариации произвольной постоянной [ 3, гл. XIII, §§ 21,23,24].
6. Нормальные системы линейных дифференциальных уравнений с постоянными коэффициентами. Метод исключения [ 3, гл. XIII, §§ 29,30].
Функции нескольких переменных
7. Функции нескольких переменных. Область определения. Предел функции. Непрерывность [ 1, гл. VIII, §§ 1-4].
8. Частные производные. Полный дифференциал и его связь с частными производными. Производная по направлению, градиент [ 1, гл. VIII, §§ 5-8, 12-16].
9. Экстремумы функции нескольких переменных. Необходимое и достаточное условие. Наибольшее и наименьшее значения [ 1, гл. VIII, §§ 17-19].
Кратные и криволинейные интегралы
10. Понятие двойного интеграла. Геометрический смысл. Свойства двойных интегралов. Вычисление двойного интеграла посредством сведения его к двукратному [ 3, гл. XIV, §§ 1-3].
11. Переход к полярным координатам в двойном интеграле [ 3, гл. XIV, § 5].
12. Геометрические и физические приложения двойного интеграла [ 3, гл. XIV, §§ 4, 8-10].
13. Понятие тройного интеграла, его геометрический смысл и свойства. Вычисление тройного интеграла посредством сведения его к трехкратному [ 3, гл. XIV, §§ 11,12].
|
|
|
14. Переход к цилиндрическим и сферическим координатам в тройном интеграле [ 3, гл. XIV, §13].
15. Геометрические и физические приложения тройного интеграла [ 3, гл. XIV, § 14].
16. Понятие криволинейного интеграла, его свойства. Вычисление криволинейного интеграла посредством сведения его к определенному [ 3, гл. XV, § 1,2].
17. Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования [ 3, гл. XV, §§ 3-4].
18. Приложения криволинейного интеграла [ 3, гл.XV, § 2].
19. Понятие поверхностного интеграла, его свойства. Вычисление поверхностного интеграла путем сведения его к двойному интегралу. Приложения поверхностного интеграла [ 3, гл. XV, §§ 6].
20. Формула Стокса [ 3, гл. XV, § 7].
21. Формула Остроградского-Гаусса [ 3, гл. XV, § 8].
22. Элементы теории поля [ 3, гл. XV, § 9].
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ №3
1. Дайте определение дифференциального уравнения. Как определяется порядок дифференциального уравнения?
2. Дайте определение общего и частного решений дифференциального уравнения.
3. Сформулируйте задачу Коши.
4. Дайте классификацию дифференциальных уравнений 1-го порядка и укажите способы их решения.
5. Приведите типы дифференциальных уравнений второго порядка, допускающих понижение порядка и укажите способы понижения порядка таких уравнений.
6. Дайте определение линейного дифференциального уравнения второго порядка. Сформулируйте теорему об общем решении такого уравнения.
7. Как находится общее решение линейного однородного уравнения второго порядка с постоянными коэффициентами?
8. Как находится частное решение неоднородного уравнения с правой частью специального вида?
9. Как находится решение неоднородного уравнения методом вариации произвольной постоянной?
10. Запишите систему линейных дифференциальных уравнений с постоянными коэффициентами. Как находится общее решение таких систем методом исключения?
|
|
|
11. Дайте определения функции двух переменных, ее области определения и непрерывности.
12. Дайте определения частных производных функции двух переменных.
13. Запишите формулу полного дифференциала для функции двух переменных.
14. Дайте определения производной по направлению и градиента функции двух переменных.
15. Сформулируйте необходимые и достаточные условия экстремума функции двух переменных.
16. Как вычисляются наибольшее и наименьшее значения функции двух переменных в замкнутой области?
17. Дайте определение двойного интеграла в прямоугольной системе координат.
18. Запишите формулу преобразования двойного интеграла от прямоугольных координат к полярным координатам.
19. Запишите формулу вычисления площади плоской фигуры и объема тела с помощью двойного интеграла.
20. Дайте определение тройного интеграла в прямоугольной системе координат.
21. Запишите формулу преобразования тройного интеграла от прямоугольных координат к цилиндрическим и сферическим координатам.
22. Запишите формулу вычисления объема тела с помощью тройного интеграла.
23. Дайте определение криволинейного интеграла.
24. Запишите формулу вычисления криволинейного интеграла посредством сведения его к определенному.
25. Запишите формулу Грина.
26. Дайте определение поверхностного интеграла.
27. Запишите формулу вычисления поверхностного интеграла путем сведения его к двойному интегралу.
28. Запишите формулы Стокса и Остроградского-Гаусса.
29. Дайте определение ротора, дивергенции, циркуляции.
КОНТРОЛЬНАЯ РАБОТА №3
Задача №1
Найти общее решение уравнения
1. 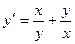 2.
2. 
3. 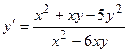 4.
4. 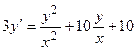
5. 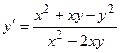 6.
6. 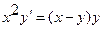
7. 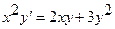 8.
8. 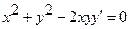
9.  10.
10. 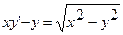
11.  12.
12. 
13. 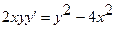 14.
14. 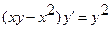
15. 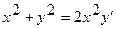 16.
16. 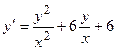
17. 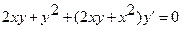 18.
18. 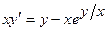
19. 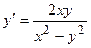 20.
20. 
Задача №2
Найти частное решение уравнения, удовлетворяющее начальному условию 
1. 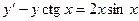 ,
,  .
.
2.  ,
, 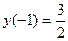 .
.
3.  ,
, 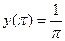 .
.
4.  ,
,  .
.
5. 
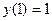 .
.
6. 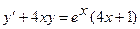 ,
,  .
.
7. 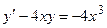 ,
, 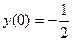 .
.
8. 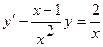 ,
, 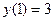 .
.
9. 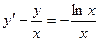 ,
, 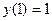 .
.
10. 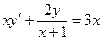 ,
, 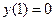 .
.
11. 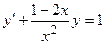 ,
, 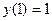 .
.
12. 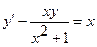 ,
,  .
.
13.  ,
, 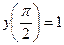 .
.
14. 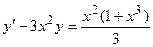 ,
, 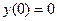 .
.
15.  ,
,  .
.
16. 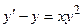 ,
, 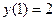 .
.
17. 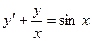 ,
, 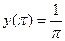 .
.
18. 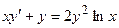 ,
, 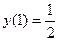 .
.
19. 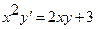 ,
, 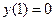 .
.
20.  ,
,  .
.
Задача №3
Найти общее решение дифференциального уравнения
1.  2.
2. 
3. 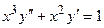 4.
4. 
5.  6.
6. 
7. 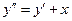 8.
8. 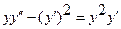
9. 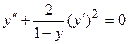 10.
10. 
11. 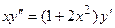 12.
12. 
13.  14.
14. 
15. 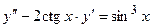 16.
16. 
17. 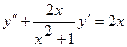 18.
18. 
19. 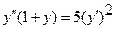 20.
20. 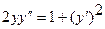
Задача №4
Найти общее решение дифференциального уравнения
1. 
2. 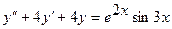
|
|
|
3. 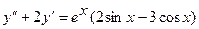
4. 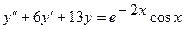
5. 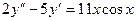
6. 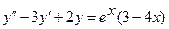
7. 
8. 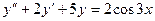
9. 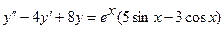
10. 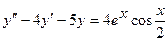
11. 
12. 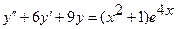
13. 
14. 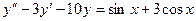
15. 
16. 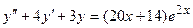
17. 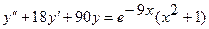
18. 

19. 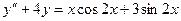
20. 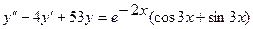
Задача №5
Методом исключения найти общее решение системы дифференциальных уравнений
1. 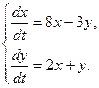 2.
2. 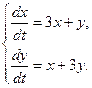
3.  4.
4. 
5. 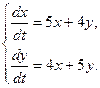 6.
6. 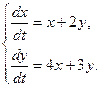
7.  8.
8. 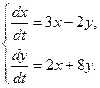
9. 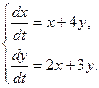 10.
10. 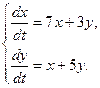
11.  12.
12. 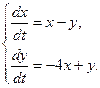
13. 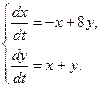 14.
14. 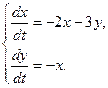
15. 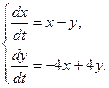 16.
16. 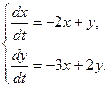
17. 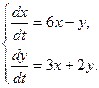 18.
18. 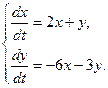
19. 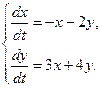 20.
20. 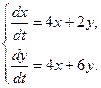
Задача №6
Найти частные производные второго порядка функции 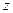
1. 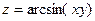 2.
2. 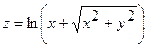
3. 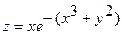 4.
4. 
5.  6.
6. 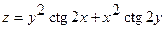
7. 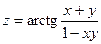 8.
8. 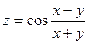
9.  10.
10. 
11. 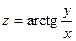 12.
12. 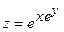
13. 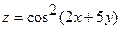 14.
14. 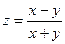
15. 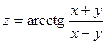 16.
16. 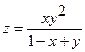
17. 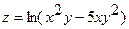 18.
18. 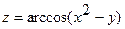
19. 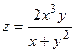 20.
20. 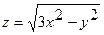
Задача № 7
Найти наибольшее и наименьшее значения функции 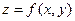 в замкнутой области
в замкнутой области
1. 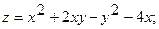
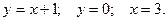
2. 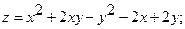
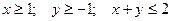 .
.
3. 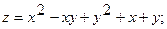
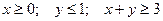 .
.
4. 
 .
.
5. 
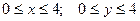 .
.
6. 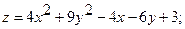
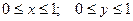 .
.
7. 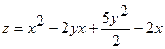 ;
;  .
.
8. 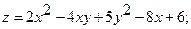
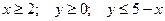 .
.
9. 
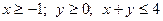 .
.
10. 
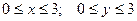 .
.
11. 
 .
.
12. 
 .
.
13. 
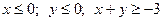 .
.
14. 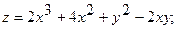
 .
.
15. 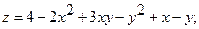
 .
.
16. 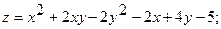
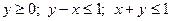 .
.
17. 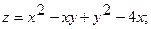
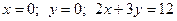 .
.
18. 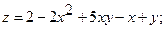
 .
.
19. 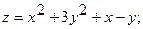
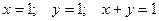 .
.
20. 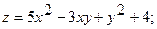
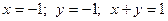 .
.
Задача №8
Даны: функция 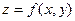 , точка
, точка  и вектор
и вектор  . Найти: 1) grad z в точке
. Найти: 1) grad z в точке  ; 2) производную в точке
; 2) производную в точке  по направлению вектора
по направлению вектора 
1. 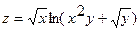 ;
;  (1;1);
(1;1); 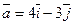 .
.
2.  ;
;  (1;1);
(1;1); 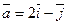 .
.
3. 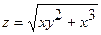 ;
;  (1;1);
(1;1); 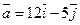 .
.
4. 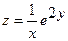 ;
;  (1;0);
(1;0); 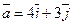 .
.
5. 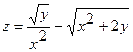 ;
;  (1;3);
(1;3); 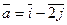 .
.
6.  ;
;  (1;-2);
(1;-2);  .
.
7. 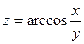 ;
;  (4;5);
(4;5); 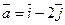 .
.
8.  ;
;  (0;1);
(0;1); 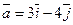 .
.
9. 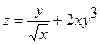 ;
;  (1;-1);
(1;-1);  .
.
10. 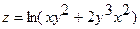 ;
;  (1;-2);
(1;-2); 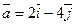 .
.
11. 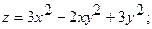
 (1;1);
(1;1); 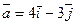
12. 
 (2;1);
(2;1); 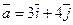 .
.
13. 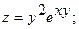
 (0;1);
(0;1); 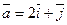 .
.
14. 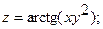
 (-1;2);
(-1;2); 
15. 
 (2;-1);
(2;-1); 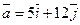
16. 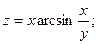
 (2;3);
(2;3); 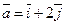 .
.
17.  ;
;  (0;2);
(0;2); 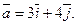
18. 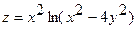 ;
;  (-1;-1);
(-1;-1); 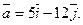
19. 
 (0;1);
(0;1); 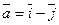 .
.
20. 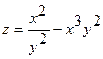 ;
;  (1;2);
(1;2); 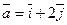 .
.
Задача № 9
Вычислить объем тела, ограниченного поверхностями
1. 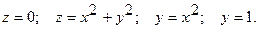
2. 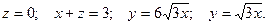
3. 
4. 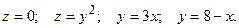
5. 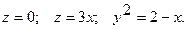
6. 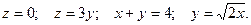
7. 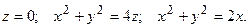
8. 
9. 
10. 

11. 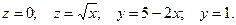
12. 
13. 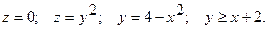
14. 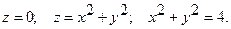
15. 
16. 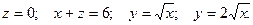
17. 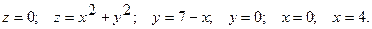
18. 
19. 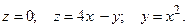
20. 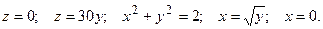
Задача № 10
1. Вычислить криволинейный интеграл 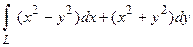 вдоль верхней половины эллипса
вдоль верхней половины эллипса  , обходя ее против хода часовой стрелки.
, обходя ее против хода часовой стрелки.
2. Вычислить криволинейный интеграл 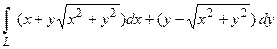 вдоль верхней половины окружности
вдоль верхней половины окружности  обходя ее против хода часовой стрелки.
обходя ее против хода часовой стрелки.
3. Вычислить криволинейный интеграл 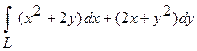 вдоль дуги L параболы
вдоль дуги L параболы 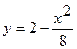 точки
точки 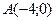 до точки
до точки 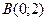 .
.
4. Вычислить криволинейный интеграл  , если L -отрезок прямой от точки
, если L -отрезок прямой от точки 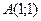 до точки
до точки 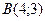 .
.
5. Вычислить криволинейный интеграл 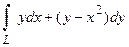 , если L -дуга параболы
, если L -дуга параболы  , расположенная над осью OX и пробегаемая против хода часовой стрелки
, расположенная над осью OX и пробегаемая против хода часовой стрелки
6. Вычислить криволинейный интеграл 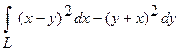 , если L -ломаная линия OAB, где
, если L -ломаная линия OAB, где 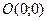 ,
,  ,
, 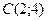 .
.
7. Вычислить криволинейный интеграл 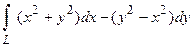 от точки
от точки 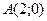 до точки
до точки 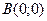 вдоль ломаной линии, состоящей из отрезков прямых
вдоль ломаной линии, состоящей из отрезков прямых 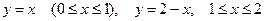 .
.
8. Вычислить криволинейный интеграл 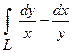 , если L -первая четверть окружности
, если L -первая четверть окружности  , пробегаемая против хода часовой стрелки.
, пробегаемая против хода часовой стрелки.
9. Вычислить криволинейный интеграл 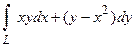 , если L -ломаная линия ABCD, соединяющая точка
, если L -ломаная линия ABCD, соединяющая точка  ,
,  ,
,  ,
,  .
.
10. Вычислить криволинейный интеграл 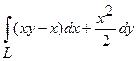 вдоль дуги L кривой
вдоль дуги L кривой 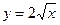 от точки
от точки  до точки
до точки  .
.
11. Вычислить криволинейный интеграл 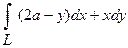 вдоль дуги L первой арки циклоиды
вдоль дуги L первой арки циклоиды 
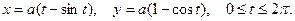
|
|
|
12. Вычислить криволинейный интеграл 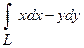 вдоль дуги L астроиды
вдоль дуги L астроиды  .
.
13. Вычислить криволинейный интеграл 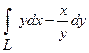 вдоль дуги L кривой
вдоль дуги L кривой  от точки
от точки  до точки
до точки  .
.
14. Вычислить криволинейный интеграл 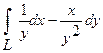 вдоль границы треугольника ABC, обходя ее против хода часовой стрелки, где
вдоль границы треугольника ABC, обходя ее против хода часовой стрелки, где  ,
, 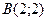 ,
, 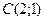 .
.
15. Вычислить криволинейный интеграл вдоль верхней 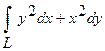 половины L эллипса
половины L эллипса 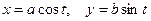 , обходя ее против часовой стрелки.
, обходя ее против часовой стрелки.
16. Вычислить криволинейный интеграл 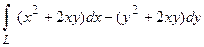 вдоль ломаной линии L = ABC, где
вдоль ломаной линии L = ABC, где  ,
, 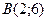 ,
, 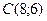 .
.
17. Вычислить криволинейный интеграл  если L -отрезок прямой от точки
если L -отрезок прямой от точки  до точки
до точки 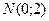 .
.
18. Вычислить криволинейный интеграл  вдоль дуги L кривой
вдоль дуги L кривой  от точки A( 1;0 ) до точки B (e;1 ).
от точки A( 1;0 ) до точки B (e;1 ).
19. Вычислить криволинейный интеграл 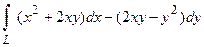 вдоль дуги L параболы
вдоль дуги L параболы 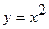 от точки
от точки  до точки
до точки  .
.
20. Вычислить криволинейный интеграл 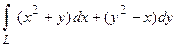 от точки
от точки 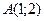 до точки
до точки 
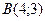 вдоль ломаной линии, состоящей из отрезков прямых
вдоль ломаной линии, состоящей из отрезков прямых  ,
, 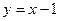 .
.
|
|
|


