 |
Примеры решения задач к контрольной работе №3
|
|
|
|
Пример 1. Решить уравнение 
.
Решение. Разделим обе части уравнения на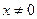 
. Получим
.
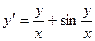Полученное уравнение имеет вид 
, где 
и 
. Правая часть уравнения является функцией одной переменной, следовательно, решаемое уравнение - однородное. Сделаем замену 
, тогда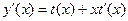 
и уравнение принимает вид 
, где 
-новая неизвестная функция. Осталось решить уравнение 
или 
Правая часть этого уравнения представляет собой произведение двух функций 
и 
зависит только от 
, 
-только от 
, это уравнение с разделяющимися переменными. Для его решения разделим переменные. Умножая уравнение на 
и деля на 
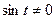, получим 
. Интегрируя последнее равенство, найдем 
(произвольную постоянную можно обозначить не 
, а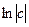 
). Тогда 
, т.е. 
; 
.
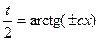Возвращаясь к исходной неизвестной функции, имеем 
.
Пример 2. Решить уравнение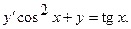 
Решение. Разделим уравнение на 
Получим уравнение вида 
, где 
т.е. линейное уравнение первого порядка. Будем его решать методом Бернулли, т.е. искать решение 
в виде 
, где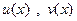 
подлежат определению. Поскольку 
, то уравнение принимает вид 
В качестве 
возьмем любую функцию, обращающую в ноль сомножитель при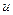 
, т. е. частное решение уравнения 
Это уравнение с разделяющимися переменными, поэтому, умножая его на и деля на 
, получим
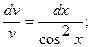
т. е. 
. Следовательно, 
(произвольная постоянная не добавляется, так как берется частное решение).
Поставим найденное v в исходное уравнения, тогда второе слагаемое в правой части обратится в ноль, и для 
получим уравнение
; 
.
Отсюда, используя формулу интегрирования по частям, найдем
Возвращаясь к исходной неизвестной функции , находим решение:
Пример 3. Решить уравнение
Решение. Уравнение имеет вид 
где 
, т.е. это уравнение Бернулли. Решение уравнения будем искать в виде . Поскольку , то уравнение примет вид
|
|
|
Возьмем в качестве любую функцию, обращающую в ноль второе слагаемое левой части, т.е. частное решение уравнения 
. Это уравнение с разделяющимися переменными. Его решение имеет вид 
Подставляя найденное в исходное уравнение, получим
Опять получили уравнение с разделяющимися переменными, решение которого
Возвращаясь к исходной неизвестной функции , находим решение
Некоторые типы уравнений второго порядка приводятся к уравнениям первого порядка. К ним относятся:
1) Уравнения вида 
, которые не содержат явным образом 
. Обозначим производную 
через 
т.е.
Тогда 
Подставляя эти выражения производных в исходное уравнение, получим уравнение первого порядка.
2) Уравнения вида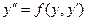 
, которые не содержат явным образом 
.
Положим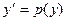 
и, так как 
то для определения производной применим правило дифференцирования сложной функции
Подставляя выражения производных в исходное уравнение, получим уравнение первого порядка относительно вспомогательной функции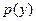 
.
Пример 4. Решить уравнение 
.
Решение. Вводим новую функцию 
, 
, тогда 
. Подставив ее в уравнение, имеем
.
Это линейное уравнение первого порядка относительно 
и его решение разыскиваем в виде произведения 
Учитывая требования 
, 
, находим функцию : 
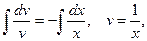подставляем в уравнение для определения
Отсюда
.
Таким образом, 
, и можно найти функцию y
, 
Пример 5. Найти общий интеграл уравнения 
.
Решение. Уравнение не содержит явным образом . Следовательно, допускается понижение порядка. Обозначим 
Тогда 
.
Получим уравнение с разделяющимися переменными 
, интегрируя которое, находим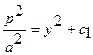 
или
Откуда 
Решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами и непрерывной правой частью вида
(1)
ищется в виде суммы 
, где 
-частное решение исходного уравнения (1), а 
-общее решение соответствующего однородного уравнения
|
|
|
. (2)
Вид общего решения 
определяется корнями характеристического уравнения. Вид частного решения - видом правой части 
уравнения (1).
1) Пусть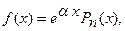 
(3)
где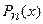 
- многочлен 
-ой степени. Тогда существует частное решение вида 
, где 
, а 
принимает одно из трех возможных значений 0, 1, 2:
2) Пусть правая часть уравнения (1) может быть представлена в виде
(4)
где и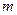 
степени многочленов 
и 
. Тогда существует частное решение вида
(5)
где 
, 
-полные многочлены степени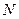 
, а принимает одно из двух значений 0 или 1:
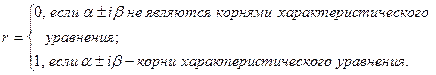
Если правая часть уравнения (1) может быть представлена в виде суммы функций (3), (4), т. е. 
, то частное решение уравнения ищется в виде суммы 
, где 
-частное решение уравнения 
, а 
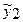-частное решение уравнения 
.
Пример 6. Найти общее решение дифференциального уравнения
Решение. Общее решение уравнения имеет вид 
, где -общее решение однородного уравнения 
. Составляем и решаем характеристическое уравнение
-частное решение исходного уравнения, которое определяем по виду правой части 
Здесь 
следовательно
25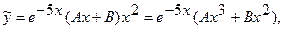 
10 
1 
Для определения коэффициентов А и В нужно решение и его производные подставить в исходное уравнение. Для этого умножаем 
соответственно на 
, 
и 
(коэффициенты уравнения) и складываем. Затем приравниваем коэффициенты при в одинаковых степенях, представив правую часть уравнения в виде
,
,
,
.
Решая полученную систему, найдем 
, 
. Следовательно,
.
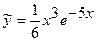Общее решение заданного уравнения имеет вид
.
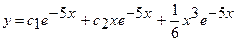Система дифференциальных уравнений вида
где 
, 
, …, 
- неизвестные функции независимой переменной , называется нормальной системой.
Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно , , …, , то система дифференциальных уравнений называется линейной.
Иногда, нормальную систему дифференциальных уравнений удается свести к одному уравнению -го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
Рассмотрим этот метод на конкретных примерах.
|
|
|
Пример 7. Найти общее системы дифференциальных уравнений
Решение. Продифференцируем по первое уравнение: 
. Подставляя сюда выражения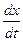 
и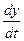 
из системы, получим
или имеем 
. Характеристическое уравнение
имеет корни 
. Следовательно, общее решение для запишется в виде
Общее решение для находим из первого уравнения:
.
Пример 8. Найти общее системы дифференциальных уравнений
Решение. Продифференцируем по первое уравнение: 
. Исключая из полученного уравнения 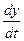, имеем 
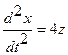. Еще раз продифференцируем по полученное уравнение второго порядка: 
. Исключая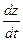 
, получим
,
т.е. мы пришли к уравнению с одной неизвестной функцией. Решив это линейное однородное уравнение третьего порядка, получим
.
Общее уравнение для получим из первого уравнения системы:
или
.
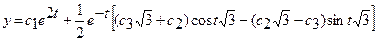Из второго уравнения системы найдем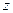 
:
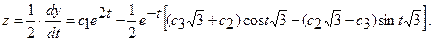
Пример 9. Найти частные производные второго порядка функции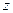
Решение. Рассматривая, как постоянную величину, получим
Аналогично, рассматривая как постоянную величину, получим
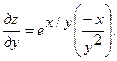
Так же находим и производные второго порядка
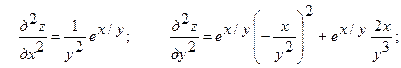
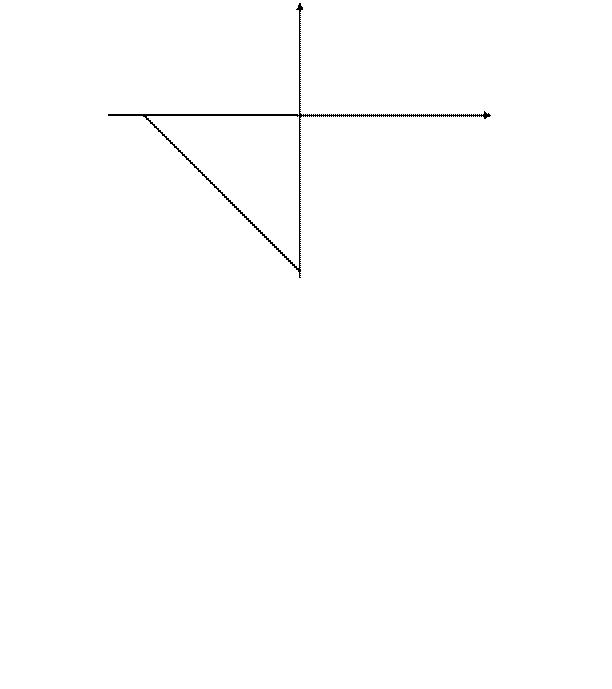
Пример 10. Найти наибольшее и наименьшее значения функции в замкнутой области
Решение. Указанная область есть треугольник АВС (рис.1). Функция, дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения или в стационарной точке, или на границе области.
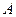-1 
-3
-1
-3 
Рис. 1
Найдем стационарные точки из условия 
В нашем случае 
Решая систему уравнений, получим 
. Точка 
является стационарной. Находим 
Исследуем функцию на границах. На линии 
: 
, 
. Задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на отрезке [-3,0].
- стационарная точка функции одной переменной. Вычисляем 
На линии 
: 
; 
- cтационарная точка. Вычисляем 
На линии 
: 
и 
; 
-стационарная точка, 
Сопоставляя все полученные значения функции 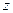, заключаем, что 
в точках 
и С (0;-3), 
в точке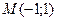 
.
Пример 11. Даны: функция 
, точка 
и вектор 
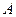. Найти: 1) grad z в т. ; 2) производную в точке 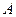по направлению вектора
|
|
|
Решение. 1) Градиент функции 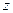имеет вид
grad 
.
Вычисляем частные производные в точке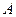
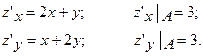
Таким образом, grad z 
2) Производная по направлению вектора , определяется по формуле
где 
- угол, образованный вектором с осью 
. Тогда
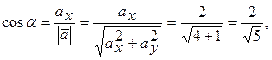
Используя значения производных в точке , найденные ранее, получим
Пример 12. Вычислить объем тела, ограниченного поверхностями
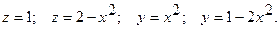
Решение. Если область определена неравенствами
то объем тела 
находится по формуле
Для определения пределов интегрирования сделаем чертеж данного тела и его проекции на плоскость XOY (рис 2а и 2б).
Следует обратить внимание на то, что для переменной x границами являются наибольшее и наименьшее значения в заданной области, т.е. 
.
Рис. 2а
Переменная y является функцией переменной x. На рисунке видно, что область D ограничена снизу кривой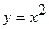 
, а сверху – кривой 
. Следовательно, 
.
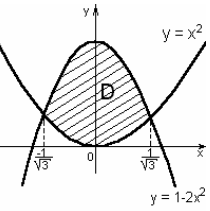
Рис.2б
Аналогично, из рисунка тела видно, что оно снизу ограничено плоскостью 
, а сверху поверхностью 
. Таким образом, переменная z является функцией двух переменных x и y, и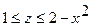 
Пример 13. Вычислить объем тела, ограниченного поверхностями
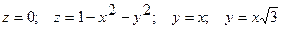
и расположенного в первом октанте
Решение. Данное тело ограничено сверху параболоидом 
. Область интегрирования 
- круговой сектор, ограниченный дугой окружностью 
, являющейся линией пересечения параболоида с плоскостью 
, и прямыми 
и 
. Следовательно,
.
Поскольку областью интегрирования является часть круга, а подынтегральная функция зависит от 
, целесообразно перейти к полярным координатам. Преобразование двойного интеграла от прямоугольных координат , к полярным координатам 
, связанным с прямоугольными координатами соотношениями 
, 
, осуществляется по формуле
.
Уравнение окружности в этих координатах примет вид 
, подынтегральная функция равна 
, а пределы интегрирования по 
определяем из уравнений прямых: 
, т.е. 
; 
, т.е. 
. Таким образом, имеем
Пример 14. Вычислить криволинейный интеграл 
вдоль 1) ломаной 
от точки 
до точки 
, где 
;2) дуги эллипса 
Решение. Пусть кривая L задана уравнениями в параметрической форме 
. Пусть точкам M и P этой кривой соответствуют значения параметра t 
соответственно. Тогда 
Если кривая задана уравнением 
, причем точке M соответствует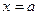 
, а точке P - 
, то
1) Криволинейный интеграл вдоль ломаной L можно разбить на сумму двух интегралов: вдоль отрезков AB и BC. Запишем уравнение прямой, проходящей через две точки A и B
Найдем производную 
Уравнение отрезка BC имеет вид 
. В этом случае 
Таким образом,
3) Кривая задана в параметрическом виде. Найдем производные
.
Тогда
|
|
|
ПРИЛОЖЕНИЕ 1
Таблица производных простейших элементарных функций.
I. (С)¢ = 0.
II. 
в частности 
III. (log а х)¢ = 
log а е, в частности (ln х)¢ = .
IV. 
в частности, 
V. (sin х)¢ = cos х.
VI. (cos х)¢ = - sin х.
vii. (
)¢ = 
VIII. (ctg x)¢= 
IX. (arcsin х)¢ = 
.
X. (arccos x)¢ =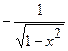 
.
XI.(arctg x)¢ = 
.
XII. (arcctg x)¢ = 
.
XIII. (sh х)¢ = ch х.
XIV. (ch х)¢ = sh х.
XV. (th x) ¢ =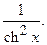 
XVI. (cth x) ¢ = 
ПРИЛОЖЕНИЕ 2
Таблица интегралов простейших элементарных функций
I. 
II. 
III. 
IV. 
V. 
VI. 
VII.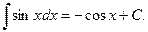 
VIII. 
IX. 
X. 
XI. 
.
XII. 
XIII. 
XIV. 
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. - М.: Наука, 1985. Т.1. 432 с..
2. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. шк., 1986. Ч. 2.
3. Пискунов Н. С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. - М.: Наука, 1978. Т. 2. 575 с.
4. Бугров Я.С. Дифференциальные уравнения. Кратные интегралы. Функции комплексного переменного / Я.С.Бугров, С.М. Никольский. – М.: Наука, 1985.
5. Кузнецов Л.А. Сборник заданий по высшей математике / Л.А. Кузнецов. - М.: Высш. шк., 1994. 172 с.
СОДЕРЖАНИЕ
| 1. | Общие рекомендации студенту-заочнику к изучению курса математики................................. | ||||
| 2. | Правила выполнения и оформления контрольных работ | ||||
| 3. | Программа курса “Математика” для студентов- заочников инженерно-технических специальностей.... | ||||
| 4. | Вопросы для самопроверки к контрольной работе № 3. | ||||
| 5. | Контрольная работа № 3......................... | ||||
| 6. | Примеры решения задач к контрольной работе № 3.... | ||||
| Приложение 1................................... | |||||
| Приложение 2................................... | |||||
| Библиографический список....................... | |||||
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к контрольной работе № 3
по математике для студентов
инженерно–технических специальностей
заочной формы обучения
Составители:
Бырдин Аркадий Петрович
Иохвидов Евгений Иосифович
Сидоренко Александр Алексеевич
Томилов Марк Федорович
В авторской редакции
Компьютерный набор А.А. Сидоренко
Подписано в печать 15.04.2016.
Формат 60´84/16. Бумага для множительных аппаратов.
Усл. печ. л. 3,3. Уч.-изд. л. 3,1. Тираж 150 экз. “C”.
Зак. №
ФГБОУ ВО “Воронежский государственный технический университет”
394026 Воронеж, Московский просп., 14
|
|
|
