 |
Формулы двойного и половинного угла
|
|
|
|
Формулы двойного угла позволяют выразить тригонометрические функции произвольного угла через функции угла в два раза меньше исходного. Эти формулы являются следствиями формул суммы двух углов, если положить в них углы равными друг другу.
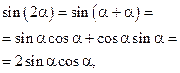
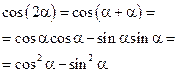
Последнюю формулу можно преобразовать с помощью основного тригонометрического тождества:
или
Таким образом, для косинуса двойного угла существует три формулы:
Следует отметить, что данная формула справедлива только при 
и 
, 
.
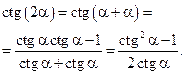
Последняя формула справедлива при 
, .
Аналогично функциям двойного угла могут быть получены функции тройного угла. Здесь данные формулы приводятся без доказательства:
,
,
,
.
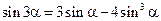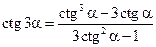Формулы половинного угла являются следствиями формул двойного угла и позволяют выразить тригонометрические функции некоторого угла через функции угла в два раза больше исходного.
Произведем следующие преобразования:
,
и выразим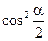 
через 
:
.
Аналогичные преобразования произведем для 
:
,
.
Последние две формулы носят названия формул понижения степени.
Выведем формулу для 
:
.
Аналогично
.
Универсальная тригонометрическая подстановка
Эта группа формул позволяет выражать значения всех тригонометрических функций через тангенс половинного угла. Данные формулы часто используются при решении уравнений и произведении преобразований.
Для того, чтобы выразить через 
воспользуемся ранее выведенной формулой:
,
,
,
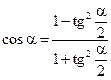при 
, .
Далее используя формулу 
и только что выведенное соотношение для косинуса получим зависимость между 
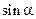и :
последняя формула также имеет смысл при , .
Формулы для тангенса и котангенса получаются при помощи формул двойного угла:
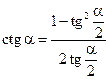при , , ,
|
|
|
при , .
Формулы произведения тригонометрических функций
Данная группа формул является следствием формул суммы и разности двух углов.
Теорема 5. Для любых вещественных 
и 
справедливы следующие соотношения:
,
.
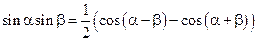
Доказательство. Запишем формулы косинуса и синуса суммы и разности для углов и :
, (1)
, (2)
, (3)
. (4)
Произведем следующие преобразования:
((1)-(2))/2:
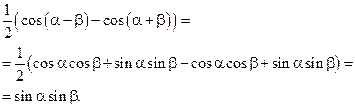
((1)+(2))/2:
((3)+(4))/2:
Что и требовалось доказать.
Формулы суммы и разности тригонометрических функций
Эти формулы также являются следствием формул суммы и разности двух углов.
Для получения формул суммы и разности функций заметим, что любые углы и можно представить следующим образом:
,
.
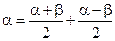Найдем сумму синусов двух произвольных углов и :
Найдем разность синусов двух произвольных углов и :
Найдем сумму косинусов двух произвольных углов и :
Найдем разность косинусов двух произвольных углов и :
Найдем сумму и разность тангенсов двух углов и , таких что , 
, 
:
Найдем сумму и разность котангенсов двух углов и , таких что 
, 
, :
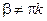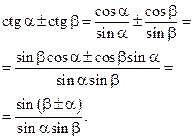
Формула дополнительного (вспомогательного) аргумента
Рассмотрим выражение вида
,
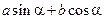в котором числа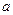 
и 
не равны нулю одновременно. Домножим и поделим каждое из слагаемых на 
и вынесем общий множитель за скобки:
Нетрудно проверить, что
,
а значит по Теореме 2 существует такой вещественный угол 
, что
и 
.
Таким образом, используя формулу синуса суммы, получаем
Формула
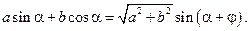
где такой угол, что и , носит название формулы вспомогательного аргумента и используется при решении неоднородных линейных уравнений и неравенств.
Обратные тригонометрические функции
Определения
До сих пор мы решали задачу определения тригонометрических функций заданных углов. А что если стоит обратная задача: зная какую-либо тригонометрическую функцию определить соответствующий ей угол.
Арксинус
Рассмотрим выражение 
, где 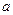– известное вещественное число. По определению синуса это есть ордината точки пересечения луча, образующего угол 
с осью абсцисс и тригонометрической окружности. Таким образом, для решения уравнения надо найти точки пересечения прямой 
и тригонометрической окружности.
|
|
|
Очевидно, что при 
прямая и окружность не имеют общих точек, а значит и уравнение не имеет решений. То есть нельзя найти угол, синус которого был бы по модулю больше 1.
При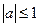 
прямая и окружность имеют точки пересечения, например, 
и 
(см. рис.). Таким образом, заданный синус будут иметь 
, 
и все углы, отличающиеся от них на целое количество полных оборотов, т.е. 
, 
, – бесконечное множество углов. Как выбрать один угол среди этого бесконечного множества?
Чтобы однозначно определить угол , соответствующий числу 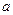, приходится требовать выполнения дополнительного условия: этот угол должен принадлежать отрезку 
. Такой угол называют арксинусом числа .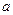
Арксинусом действительного числа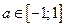 
называется действительное число 
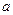
, синус которого равен . Такое число обозначают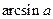 
.
Арккосинус
Рассмотрим теперь уравнение вида 
. Для его решения необходимо найти на тригонометрической окружности все точки, имеющие абсциссу 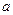, т.е. точки пересечения с прямой 
. Как и в предыдущем случае при рассматриваемое уравнение не имеет решений. А если 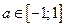, имеются точки пересечения прямой и окружности, соответствующие бесконечному множеству углов , , .
Чтобы однозначно определить угол , соответствующий данному косинусу, вводят дополнительное условие: этот угол должен принадлежать отрезку 
; такой угол называют арккосинусом числа .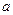
Арккосинусом действительного числа 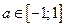называется действительное число 
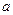
, косинус которого равен . Такое число обозначают 
.
Арктангенс и арккотангенс
Рассмотрим выражение 
. Для его решения надо найти на окружности все точки пересечения с прямой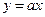 
, угловой коэффициент которой равен тангенсу угла наклона прямой к положительному направлению оси абсцисс. Такая прямая при всех действительных значениях 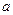пересекает тригонометрическую окружность в двух точках. Эти точки симметричны относительно начала координат и соответствуют углам , , .
Для однозначного определения угла с заданным тангенсом его выбирают из интервала 
.
|
|
|
Арктангенсом произвольного действительного числа 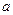называется действительное число 
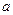
, тангенс которого равен . Такое число обозначают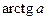 
.
Для определения арккотангенса угла используются аналогичные рассуждения, с той лишь разницей, что рассматривается пересечение окружности с прямой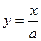 
и угол выбирается из интервала 
.
Арккотангенсом произвольного действительного числа 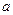называется действительное число 
, котангенс которого равен 
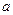
. Такое число обозначают 
.
|
|
|
