Обработка результатов прямых измерений.

АЛЬМЕТЬЕВСКИЙ ГОСУДАРСТВЕННЫЙ

НЕФТЯНОЙ ИНСТИТУТ

Кафедра автоматизации и информационных технологий

И.П.Ситдикова, Р.Р.Ахметзянов, Р.Б.Булатов

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К самостоятельному изучению и выполнению контрольной работы по

«Метрологии, стандартизации и сертификации»

Для студентов заочного обучения

Альметьевск – 2010г

УДК 531.7

Б31

 

 

Составители: Булатов Р.Б., Ахметзянов Р.Р., Ситдикова И.П.

 

Методические указания к самостоятельному изучению и выполнению контрольной работы по дисциплине «Метрология, стандартизация и сертификация» для студентов очного и заочного форм обучения.

Альметьевск: издательство Альметьевского государственного нефтяного института, 2010.-33с.

 

 

Изложен порядок самостоятельной работы студентов над материалами дисциплины и приведены варианты контрольных работ, которые выполняются студентами – заочниками в результате ее изучения.

 

Рекомендованы к внутривузовскому пользованию решением учебно-методического совета АГНИ от 29 октября 2001 г. (протокол№2).

 

Общие требования

 

Дисциплина метрология, стандартизация и сертификация ставит своей целью дать будущим инженерам нефтегазовой промышленности необходимые теоретические и практические навыки в области метрологического обеспечения, стандартизации и сертификации, являющихся основными инструментами достижения высокого качества продукции, услуг и работ.

Настоящее методическое пособие разработано в соответствии с требованиями Государственного образовательного стандарта, учебного плана и рабочей программой, утверждённой кафедрой автоматизации и информационных технологий АГНИ.

При работе над дисциплиной студент должен ознакомиться с содержанием каждой темы по рабочей программе и настоящим методическими указаниями, изучить учебный материал по рекомендованным источникам литературы и кратко законспектировать его. Для проверки учебного материала дать ответы на теоретические вопросы, приведённые в методических указаниях по каждой теме (таблица №1).

Если при изучении дисциплины у студента возникнут вопросы, на которые нет разъяснений в литературе, то ему следует обратится на кафедру.

Самостоятельная систематическая работа над дисциплиной завершается выполнением контрольной работы. Студент должен выполнить её в соответствии со своим вариантом, номер которого соответствует последней цифре шифра зачетной книжки студента.

Контрольный работы, выполненные не по варианту, не рецензируются и возвращаются студенту.

Контрольная работа, оформленная по установленным правилам, должна поступить на кафедру в течение времени межсессионного периода, но не менее чем за один месяц до начала следующей сессии.

Выполнение контрольной работы является важным этапом в процессе изучения теоретического материала. Правильное решение задач является критерием усвоения материала студентом. Задачи необходимо решать самостоятельно, опираясь на проработанный теоретический материал.

Контрольная работа должна быть выполнена в срок, установленный учебным планом.

Контрольная работа состоит из теоретического (четыре вопроса) и практического заданий (шесть задач). Исходные данные для решения задач берутся из соответствующих таблиц.

При выполнении контрольной работы следует соблюдать следующие требования:

· В начале контрольной работы должны быть указаны: дисциплина, фамилия, имя, отчество студента, курс, факультет, специальность.

· Контрольная работа оформляется в тетради аккуратно. Все действия при решении выполняются в той же последовательности и под теми же номерами, как указано в тексте задачи. Расчёты должны сопровождаться чёткими пояснениями, а обозначения должны быть расшифрованы. Для численных значений ответов указываются размерности.

· Схемы, диаграммы и графики выполняются на миллиметровой бумаги.

· В конце контрольной работы даётся список литературы, которая использовалась при выполнении контрольной работы, проставляется дата выполнения работы и подпись студента.

Только положительная рецензия преподавателя на контрольную работу является основанием для допуска студента к сдаче зачёта в целом по дисциплине.

 

Задание на контрольную работу

 

№ варианта	Теоретические вопросы	Задачи (по 6 задач в каждом варианте)
	1, 31, 61,91
	2, 32, 62, 92
	3, 33, 63, 93
	4, 34, 64, 94
	5, 35, 65, 95
	6, 36, 66, 96
	7, 37, 67, 97
	8, 38, 68, 98
	9, 39, 69, 99
	10, 40, 70, 100
	11, 41, 71, 101
	12, 42, 72, 102
	13, 43, 73, 103
	14, 44, 74, 104
	15, 45, 75, 105
	16, 46, 76, 106
	17, 47, 77, 107
	18, 48, 78, 108
	19, 49, 79, 109
	20, 50, 80, 110
	21, 51, 81, 111
	22, 52, 82, 112
	23, 53, 83, 113
	24, 54, 84, 114
	25, 55, 85, 115
	26, 56, 86, 116
	27, 57, 87, 117
	28, 58, 88, 118
	29, 59, 89, 119
	30, 60, 90, 120

 

 

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ И ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

I часть. Метрология

1. Основные термины и определения в метрологии

2. Физические величины и их единицы

3. Классификация измерений

4. Основные характеристики средств измерений

5. Автоматизация средств измерений

6. Классификация эталонов

7. Примеры построения эталонов

8. Погрешности измерений

9. Динамические характеристики

10. Погрешность, вносимая измерительной системой

11. Помехи

12. Надёжность

13. Погрешности средств измерений

14. Определение погрешности результата измерений

15. Модели объекта измерений

16. Основные источники погрешности измерений

17. Нормирование метрологических характеристик средств измерений

18. Нормирование динамических погрешностей средств измерений

19. Классы точности средств измерений

20. Понятие видов и методов измерений

21. Характеристика средств измерений

22. Метрологическая надёжность средств измерений

23. Обработка результатов измерений

24. Метрологические свойства и метрологические характеристики средств измерений

25. Основы теории и методики измерений

26. Законы распределения результатов и погрешностей измерений

27. Идентификация законов распределения величин по результатам измерений

28. Рекомендуемые правила по округления результатов измерений

29. Точечные и интервальные оценки истинного значения измеряемой величины

30. Обработка результатов прямых равноточных измерений

31. Обработка результатов прямых неравноточных рядов измерений

32. Обработка результатов косвенных измерений

33. Обработка результатов совокупных и совместных измерений

34. Понятие об испытании и контроле

35. Основы метрологического обеспечения

36. Нормативно-правовые основы метрологии

37. Метрологические службы и организации

38. Понятие о надзоре и контроле

39. Государственные испытания средств измерений

40. Поверка средств измерений

41. Калибровка средств измерений

42. Метрологическая аттестация средств измерений и испытательного оборудования

43. Методики выполнения измерений

44. Применение информационной теории для оценки результатов и погрешностей измерений

45. Энтропия и информация

46. Применение основных положений теории информации для характеристик процесса измерения

47. Энтропийное значение погрешности измерений

48. Практические методы определения энтропийного значения погрешности измерений

49. О законе «Об обеспечении единства измерений»

50. Основы обеспечения единства измерений. Поверочные схемы

51. Основные понятия теории вероятностей и математической статистики

52. Законы распределения случайных величин

53. Числовые характеристики случайных величин

54. Случайные функции

55. Аппроксимация теоретических и экспериментальных законов распределения случайных величин

56. Измерение электрических величин, методы, схемы, приборы

57. Измерение неэлектрических величин. Методы, схемы, приборы

58. Магнитные материалы и их характеристики

59. Общие сведения об измерительных информационных системах

60. Критерии годности объекта контроля

 

II ЧАСТЬ. СТАНДАРТИЗАЦИЯ

61. Законодательная и правовая база стандартизации

62. Понятия стандартизация и стандарт

63. Основные понятия и определения в области стандартизации

64. Виды и методы стандартизации

65. Категории и виды стандартов

66. Основные принципы стандартизации

67. Основные стандарты ГСС

68. Основные цели ГСС

69. Цели и задачи Госстандарта России

70. Российские организации по стандартизации

71. Международные организации по стандартизации

72. Международная стандартизация

73. Этапы разработки международных стандартов

74. Стандарты, обеспечивающие качество продукции

75. Систематизация, кодирование и классификация

76. Унификация, типизация и агрегатирование машин

77. Система стандартов по управлению и информации

78. Система стандартов социальной сферы

79. Единая система классификации и кодирования технико-экономической информации как объект стандартизации

80. Стандартизация услуг

81. Эффективность работ по стандартизации

82. Государственные и отраслевые системы стандартов на общетехнические нормы, термины и определения

83. Принципы, определяющие научно-техническую организацию работ по стандартизации

84. Получения экспертных оценок

85. Стандарты отклонений геометрических параметров деталей

86. Стандарты по управленческой документации, ОРД, по информационным технологиям

87. Структура и порядок разработки отраслевого стандарта

88. Определение стандарта предприятия

89. Понятие взаимозаменяемости

90. Государственный надзор за внедрением и исполнением стандартов

 

III ЧАСТЬ. СЕРТИФИКАЦИЯ

91. Основные понятия сертификации. История развития сертификации

92. Основные цели и принципы сертификации

93. Виды сертификации

94. Система сертификации

95. Основные стадии сертификации

96. Субъекты или участники сертификации

97. Правила и документы по проведению работ в области сертификации

98. Порядок сертификации продукции

99. Нормативные документы по сертификации

100. Структура нормативно-методического обеспечения сертификации

101. Стандарты на объекты сертификации

102. Стандартизация методов оценки соответствия

103. Стандарты на органы по сертификации и испытательные лаборатории

104. Организация деятельности органов сертификации

105. Организация деятельности испытательных лабораторий

106. Аккредитация органов по сертификации и испытательных лабораторий

107. Сертификация средств производства

108. Особенности сертификации работ и услуг

109. Сертификация систем качества

110. Ответственность должностных лиц за нарушение правил сертификации

111. Ответственность за нарушение обязательных требований государственных стандартов при производстве продукции и правил сертификации

112. Состояние и перспективы развития сертификации

113. Правила и порядок сертификации систем качества

114. Основные функции органа сертификации

115. Менеджмент образцов

116. Основные этапы сертификационных испытаний

117. Определение аккредитации органов по сертификации и испытательных лабораторий

118. Этапы процесса аккредитации

119. Требования предъявляемые к органу аккредитации

120. Определение технической компетенции органа по сертификации

ЗАДАЧИ

Обработка результатов прямых измерений.

Результат измерения – числовое значение, приписываемое измеряемой величине, с указанием точности измерения.

Численные показатели точности:

· доверительный интервал (доверительные границы) погрешности;

· оценка СКО погрешности.

Правила выражения показателей точности:

· численные показатели точности выражаются в единицах измеряемой величины;

· численные показатели точности должны содержать не более двух значащих цифр

· наименьшие разряды результата измерения и численных показателей точности должны быть одинаковыми

Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины:

х₁, х₂, х₃, ……х_n (1)

Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Величину, которая будет являться такой оценкой, мы обозначим . Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx. В таком случае мы можем записать результат измерений в виде

(2)

Так как оценочные значения результата измерений и ошибки Δx не являются точными, запись (2) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (2). Сам этот интервал называется доверительным интервалом.

Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде

l = (8.34 ± 0.02) мм, (P = 0.95)

Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм.

Таким образом, задача заключается в том, чтобы, имея выборку (1), найти оценку результата измерений , его ошибку Δx и надежность P.

Эта задача может быть решена с помощью теории вероятностей и математической статистики.

В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой

(3)

где Δx – отклонение от величины истинного значения;

σ – истинная среднеквадратичная ошибка;

σ²– дисперсия, величина которой характеризует разброс случайных величин.

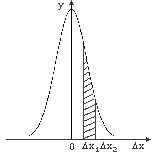
Рис.1

Как видно из (3) функция имеет максимальное значение при x = 0, кроме того, она является четной.

На рис.1 показан график этой функции. Смысл функции (4) заключается в том, что площадь фигуры, заключенной между кривой, осью Δx и двумя ординатами из точек Δx₁ и Δx₂ (заштрихованная площадь на рис.1) численно равна вероятности, с которой любой отсчет попадет в интервал (Δx₁, Δx₂).

Поскольку кривая распределена симметрично относительно оси ординат, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны. А это дает возможность в качестве оценки результатов измерений взять среднее значение всех элементов выборки (2).

(5)

где – n число измерений.

Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина стремится к истинному значению μ измеряемой величины при n → ∞.

Средней квадратичной ошибкой отдельного результата измерения называется величина

(6)

Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ

(7)

С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений.

Среднеквадратичной ошибкой среднего арифметического называется величина

(8)

Это фундаментальный закон возрастания точности при росте числа измерений.

Ошибка S _x характеризует точность, с которой получено среднее значение измеренной величины . Результат записывается в виде:

(9)

Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз.

В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n→∞ переходит в распределение Гаусса, а при малом числе отличается от него.

Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом Стьюдента t.

Опуская теоретические обоснования его введения, заметим, что

(10)

где Δx – абсолютная ошибка для данной доверительной вероятности; S_x– среднеквадратичная ошибка среднего арифметического.

Коэффициенты Стьюдента приведены в таблице 1.

Из сказанного следует:

Величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического.

При n→∞ S_x→0, т.е. интервал, в котором с заданной вероятностью находится истинное значение μ, стремится к нулю с увеличением числа измерений. Казалось бы, увеличивая n, можно получить результат с любой степенью точности. Однако точность существенно увеличивается лишь до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, т.к. конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки, взяв ее, например, равной 10% от систематической. Задавая для выбранного таким образом доверительного интервала определенное значение P (например, P = 0.95), нетрудно нейти необходимое число измерений, гарантирующее малое влияние случайной ошибки на точность результата.

Для этого удобнее воспользоваться таблицей 2, в которой интервалы заданы в долях величины σ, являющейся мерой точности данного опыта по отношению к случайным ошибкам.

Коэффициенты Стьюдента для заданных значений

Таблица №1

	0,9	0,91	0,92	0,93	0,94	0,95	0,96	0,97	0,98	0,99
	2,132	2,227	2,333	2,456	2,601	2,776	2,999	3,328	3,747	4,604
	2,015	2,008	2,191	2,298	2,422	2,571	2,757	3,003	3,365	4,032
	1,943	2,019	2,105	2,202	2,314	2,447	2,613	2,829	3,163	3,707
	1,895	1,967	2,047	2,137	2,241	2,365	2,517	2,715	2,998	3,499
	1,860	1,938	2,005	2,091	2,190	2,306	2,449	2,634	2,896	3,355
	1,833	1,900	1,973	2,056	2,151	2,262	2,399	2,574	2,821	3,250
	1,812	1,877	1,949	2,029	2,121	2,228	2,260	2,528	2,764	3,169
	1,796	1,859	1,929	2,007	2,097	2,201	2,329	2,491	2,718	3,106
	1,782	1,845	1,913	1,989	2,077	2,179	2,303	2,461	2,681	3,055
	1,771	1,832	1,899	1,974	2,061	2,160	2,282	2,436	2,650	3,012
	1,761	1,822	1,888	1,962	2,047	2,145	2,264	2,415	2,624	2,477
	1,753	1,813	1,878	1,951	2,034	2,131	2,249	2,398	2,602	2,947

 

Таблица 2

Необходимое число измерений для получения ошибки Δ с надежностью Р
Δ = Δx/σ	Значения Р
0,5	0,7	0,9	0,95	0,99	0,999
1,0
0,5
0,4
0,3
0,2
0,1

 

При обработке результатов прямых измерений предлагается следующий порядок операций:

Результат каждого измерения запишите в таблицу.

Вычислите среднее значение из n измерений

Найдите погрешность отдельного измерения

Вычислите квадраты погрешностей отдельных измерений

(Δx ₁)², (Δx ₂)²,..., (Δx _n)².

Определите среднеквадратичную ошибку среднего арифметического

Задайте значение надежности (обычно берут P = 0.95).

Определите коэффициент Стьюдента t для заданной надежности P и числа произведенных измерений n.

Найдите доверительный интервал (погрешность измерения)

Если величина погрешности результата измерения Δx окажется сравнимой с величиной погрешности прибора δ, то в качестве границы доверительного интервала возьмите

Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.

Окончательный результат запишите в виде

Оцените относительную погрешность результата измерений

ЗАДАЧА 1.

Произведено шестнадцатикратное измерение сопротивления R_x (Ом) и получены результаты таблица №1. Найти результат измерения и доверительный интервал результата с вероятностью таблица №2. Предварительно проверить, нет ли в ряду измерений промахов (грубых погрешностей)

№ варианта	Измеренные значения сопротивлений, Ом	Дов. вероят. Р
R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11	R12	R13	R14	R15	R16
	30,00	30,1	30,2	30,3	30,4	30,5	30,6	30,7	30,8	29,9	29,8	29,7					0,9
	31,00	31,2	31,01	31,02	31,05	31,06	31,6			31,8	31,7	31,8	31,9		29,8	30,89	0,91
	32,00	32,01	32,1	32,5	32,6	32,4	32,8	32,12	32,15			31,8	31,9		31,8		0,92
	33,00	33,1	33,2	33,5	33,4	33,6	33,8	33,01			32,1	32,8	31,89	31,9	32,88	32,99	0,93
	34,00	34,01	34,5	34,9	33,05	33,09		33,89	33,49			32,99	33,9			34,8	0,94
	35,00	35,06	35,04	35,09	35,07	35,02	35,12	35,13	35,48		34,89	34,99	34,78	34,88	34,9		0,95
	36,00	36,01	36,02		36,45	36,8	36,19	36,15	36,4	36,7	36,8	36,9	35,9	35,9	35,89		0,96
	37,00	37,1	37,3	37,12	37,8	37,15		37,2	37,25	37,23	37,24		37,63	37,56	37,32	37,33	0,97
	38,00	38,02	38,06	38,09		38,12	38,13	38,49	38,16		38,55	37,99		37,88		37,99	0,98
	39,00	39,1	39,5		39,66	39,46	39,47	39,2	39,1	38,98	38,99		38,95	38,94	38,8	38,7	0,97
	40,00	40,01	40,2	40,5	40,05		39,89	39,5	39,88	39,99		4,01	40,02	40,03	40,06	40,7	0,96
	41,00	41,3		41,12	41,16	41,8	41,8	41,01	41,03		39,38	39,99	40,8	40,89	40,99	41,00	0,95
	42,00	42,01	42,03		42,11	42,13	42,05	42,09		42,08	42,09	41,89	41,25	41,56	42,00	42,00	0,94
	43,00	43,5	43,05	43,02		43,00	43,5	43,6	43,7	43,8	42,19		42,89	42,98	42,76	42,00	0,93
	44,00	44,01	44,03	44,05	44,06	44,09		44,1	44,1	44,3	44,6	43,9		43,38	43,3	43,7	0,92
	45,00	45,6	45,8	45,1	45,02		45,6	45,38	45,9	44,9	44,99		45,00	44,02	45,1	45,01	0,91
	46,00	46,01	46,02	46,03		46,04	46,5	46,06	46,07	46,8		46,8	45,8	45,9	45,89	45,00	0,9
	47,00	47,01	47,02		47,03	47,06	47,1	47,2	47,6		46,9	46,8	46,5	46,8	46,00	47,00	0,91
	48,00	48,5		48,05	48,06	48,09	47,9	47,8	47,7	48,00		48,01	48,02	48,03	48,04	48,05	0,98
	49,00		49,00	49,01	49,02	49,1	49,2	49,3	49,4	49,5	49,8		48,9	48,8	48,99	49,00	0,92
	50,00	50,01		50,2	50,1	50,3	50,4	51,01	50,06	50,07		49,89	49,9	49,8	49,7	50,00	0,93
	51,00	51,01	51,02		51,1	51,2	51,3	51,04	51,08		51,14	50,89	50,98	50,68	50,00	51,00	0,94
	52,00	52,02	52,03			52,1	52,2	52,3		52,4	52,5	52,6	52,06			52,00	0,95
	53,00	53,01	53,02		53,1	53,2	53,5	53,6	53,4		53,8	53,7	53,9	53,4	53,2	52,9	0,96
	54,00	54,01		54,1	54,2	54,3	54,06	54,07	54,3	54,09		53,9	53,89	53,00	54,00	54,01	0,97
	55,00		55,02	55,06	55,1	55,4	55,8	55,6	54,8	54,9	54,89		55,00	54,89	54,98	54,79	0,98
	56,00	56,00		56,1	56,2	56,3	56,8	56,9	55,9	55,8	55,95	55,00		54,89	54,9	54,00	0,97
	57,00	57,2	57,3		57,8	57,9	56,9	56,89	56,98	56,00	57,00		57,2	57,1	51,6	57,4	0,96
	58,00	58,3	58,6	58,9		58,7	58,02	58,03	58,04	58,06		57,9	57,8	57,98	59,00	58,00	0,95
	59,00	59,01	58,9	58,98	59,03		59,1	59,4	59,7		59,6	59,4	59,2	59,00	59,3	59,06	0,94

 

ПРИМЕР

Произведено пятикратное измерение сопротивления R_x и получены результаты R_i: 5; 5,1; 5,2; 7; 5,3 Ом. Найти результат измерения и доверительный интервал результата с вероятностью таблица Р=0,98. Предварительно проверить, нет ли в ряду измерений промахов (грубых погрешностей)

Решение:

Определим среднее арифметическое значение сопротивления:

Определим оценку среднего квадратичного отклонения результатов:

Подозрительный результат (7 Ом), можно считать промахом, если R – >3· S_x

Проверяем: R – 7–5.52=1.48 Ом

3· S_x = 3·0,697=2,091

1,48>2,091 – неравенство неверно, значит результат 7 не является промахом.

Определим оценку среднего квадратичного отклонения среднего результата (результата измерений)

Для n=5 P=0.98 коэффициент Стьюдента равен: t=3.747

Доверительный интервал результата измерения:

Ом

Результат измерения запишется в виде:

Ом; Р=0,98, где R _д – действительное значение сопротивления.

Ответ: R _д =(5,52±1,054)Ом; Р=0,98; результат 7 не является промахом.

 

Размерность

Для записи количественных соотношений (законов), связывающих различные физические величины, необходимо кроме их определения указать способ измерения и единицы измерения. Способ измерения - это указание экспериментальных действий, которые необходимо выполнить, чтобы сравнить значение величины с единицей измерения и получить численное значение величины, например координаты частицы x.

В связи с построением систем единиц возникает понятие размерности. Размерность физической величины – одна из важнейших ее характеристик, которую можно определить как буквенное выражение, отражающее связь данной величины с величинами, принятыми за основные в рассматриваемой системе величин. Так, система величин, которая именуется Международной системой единиц, содержит семь основных системных величин: l, m, t, Ι, Τ, ν и J, где l – длина, m – масса, t – время, I – сила электрического тока, Τ – термодинамическая температура, ν – количество вещества, J – сила света. Для этих величин условно приняты следующие размерности: для длины – L, массы –М, времени – Т, силы электрического тока – I, термодинамической температуры – Θ, количества вещества – N и силы света – J. Размерности записывают прописными буквами и печатают прямым шрифтом [4].

Размерность величины x обозначается через dim x. Например: dim t =T; dim l =L; dim m =M. Над размерностями величин, как и над самими величинами, можно производить действия умножения, деления, возведения в степень и извлечения корня. Показатель степени, в которую возведена размерность основной величины, входящей в степенной одночлен, называют показателем размерности [4; 5].

Размерность производных физических величин определяется исходя из уравнения связи между физическими величинами. Например,

Размерность физической величины еще не определяет ее единицу. Она устанавливает только связь между единицами различных физических величин. Размерность дает правило, позволяющее определить, как меняется единица производной физической величины при изменении масштабов основных величин. Это правило, выраженное в виде математической формулы, называется формулой размерности.

dim [X]=L^β ·M^ε ·T^η ·I^σ ·J^φ ·N^α Θ^ψ

Различают как размерные, так и безразмерные физические величины. К первым относят такие величины, в размерностях которых хотя бы один из показателей размерности не равен нулю. Безразмерными физическими величинами называют физические величины, в размерностях которых все показатели размерности равны нулю.

Величины, не являющиеся основными, называются производными или вторичными. Для них единицы устанавливаются из требования, чтобы числовые коэффициенты, входящие в физические законы или формулы, служащие определением рассматриваемых величин, принимали определенные, заранее выбранные значения.

Mожно было бы для каждой физической величины установить свою единицу, никак не связанную с единицами других величин. Но тогда в уравнения, выражающие физические законы, вошло бы множество числовых коэффициентов. Их значения не укладывались бы ни в какую простую и легко запоминаемую схему, а определялись бы случайным выбором единиц. Такое множество числовых коэффициентов весьма сильно усложняло бы формулы.

ЗАДАЧА 2.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: