 |
Контрольная работа по дисциплине математика
|
|
|
|
Задание 1.
Множества A и B заданы числовыми промежутками. Найдите множества  ,
, 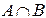 , A \ B, B \ A,
, A \ B, B \ A, 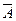 ,
,  .
.
| Вариант | Множество A | Множество B |
[–23; 0]
[–5; 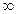 )
[–0,5; 22)
(–3; 17,5]
(– )
[–0,5; 22)
(–3; 17,5]
(– 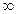 ; –4)
(–12; 6)
(– ; –4)
(–12; 6)
(– 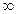 ; 10]
[–10; 0]
(–6; ; 10]
[–10; 0]
(–6; 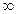 )
(– )
(– 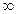 ; -19) ; -19)
| (–3,5; 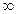 )
[0,1; 7)
[8; )
[0,1; 7)
[8; 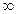 )
(9; )
(9; 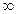 )
(–40; 13]
(– )
(–40; 13]
(– 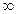 ; 2]
(–11; 3,2)
(– ; 2]
(–11; 3,2)
(– 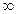 ; 11)
(– ; 11)
(– 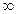 ; 15]
(– ; 15]
(– 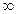 ; 10,2] ; 10,2]
|
Задача 2
Задано множество 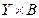 . Найдите множества Y, B,
. Найдите множества Y, B,  .
.
| Вариант | 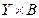
|

| |

| |

| |

| |

| |

| |

| |

| |

| |

|
Задание 3.
Из высказываний A и B образуйте дизъюнкцию, конъюнкцию, импликацию и эквиваленцию. Найдите значения истинности образованных высказываний.
| Вариант | Высказывание A | Высказывание B |
| 5 – натуральное число | 7 < 3 | |
 – целое число – целое число
| 4 > 5 | |
| 0.75 – целое число | 2 * 3 = 6 | |
| 5 – простое число | 7 + 0 = 8 | |
 - рациональное число - рациональное число
| 
| |
| –5 – целое число | 7 – 3 = 2 | |
 - иррациональное число - иррациональное число
| 3 > 5 | |
| 0,2 – натуральное число | 6 + 3 = 9 | |
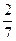 – рациональное число – рациональное число
| 2 + 1 = 5 | |
| –7 – натуральное число | 2 < 6 |
Задание 4.
1. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, Г, И, Л, М, О, Р, Т, получится слово алгоритм?
2. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, А, А, Н, Н, С, получится слово ананас?
3. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы а, А, в, к, н, о, р, т, получится слово автокран?
4. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы Е, В, И, Л, О, О, Р, С, С, Т, Т, Т, Ь, получится слово строительство?
5. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, А, А, М, Р, Р, Т, У, получится слово арматура?
|
|
|
6. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы а, в, К, л, н, о, о, т, получится слово котлован?
7. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, А, А, П, П, Х получится слово папаха?
8. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, А, Е, К, К, И, М, Р, получится слово керамика?
9. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, А, Е, И, К, Р, Р, Т, Т, У, Х, получится слово архитектура?
10. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, Д, Е, М, Н, Н, Т, У, Ф получится слово фундамент?
Задание 5
Вариант 1
Непрерывная случайная величина X задана плотностью распределения вероятностей
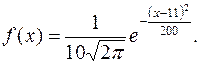
Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 2
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 3
Непрерывная случайная величина X задана плотностью распределения вероятностей
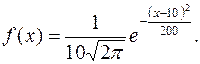
Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 4
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
|
|
|
Вариант 5
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 6
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 7
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 8
Непрерывная случайная величина X задана плотностью распределения вероятностей
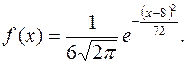
Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 9
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Вариант 10
Непрерывная случайная величина X задана плотностью распределения вероятностей

Определите математическое ожидание этой нормально распределённой величины, дисперсию, среднее квадратическое отклонение и выполните эскиз графика функции f (x).
Задание 6
Вариант 1
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,2 | 0,5 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 2
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,3 | 0,6 | 0,1 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 3
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,2 | 0,7 | 0,1 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
|
|
|
Вариант 4
Случайная величина X имеет закон распределения:
| X | – 4 | ||
| p | 0,4 | 0,3 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
| Y | |||
| p | 0,3 | 0,6 | 0,1 |
Вариант 5
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,1 | 0,7 | 0,2 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 6
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,2 | 0,5 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 7
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,2 | 0,5 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 8
Случайная величина X имеет закон распределения:
| X | – 1 | ||
| p | 0,1 | 0,6 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 9
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,3 | 0,2 | 0,5 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Вариант 10
Случайная величина X имеет закон распределения:
| X | |||
| p | 0,3 | 0,4 | 0,3 |
Найдите математическое ожидание величины, дисперсию и среднее квадратическое отклонение величины X.
Учебная литература
1. Грес П.В. Математика для гуманитариев: М: Логос., 2008. – 120 с.
2. Турецкий В. Я. Математика и информатика: учеб. пособие для вузов по гуманитарным специальностям. – М.: ИНФРА, 2006. – 560 с.
|
|
|


