 |
Сложная функция и ее производная
|
|
|
|
Задачи из основ теории вероятностей и математической статистики
91. Сколькими способами можно расставить на полке шесть различных книг?
92. Сколько пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4 без повторений?
93. Из цифр 1, 2, 3, 4, 5 сколько можно составить различных двузначных чисел при условии, что ни одна
из них не повторяется?
94. В группе из 30 студентов нужно выбрать трех дежурных. Сколькими способами это можно сделать?
95. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется?
96. Сколько сложных красок можно составить из 7 основных, если смешивать их по 3?
97. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке.
Сколькими способами это можно сделать?
98. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна
вероятность того, что этот билет выигрышный.
99. В урне 10 белых и 5 черных шаров. Наугад вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся белые?
100. В урне 4 белых и 7 черных шаров. Наугад вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся белые?
КРАТКИЕ ВОПРОСЫ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА И РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИИЮ ЗАДАНИЙ ИЗ КОНТРОЛЬНОЙ РАБОТЫ:
РАЗДЕЛ 1.1. Функция одной независимой переменной. Пределы.
Вычисление пределов:
1. Непосредственное вычисление предела:
 ;
;  .
.
2. Использование зависимостей между бесконечно малой и бесконечно большой функциями при взятии пределов:

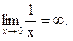


3. Раскрытие неопределенности вида: 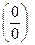
3.1. х→0 (числитель и знаменатель функции, стоящей под знаком предела разделить на х в наименьшей степени стоящей в знаменателе и вычислить предел)
|
|
|
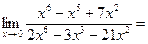
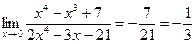 , в нашем случае делим на (х2)
, в нашем случае делим на (х2)
3.2 х→а (числитель и знаменатель функции, стоящей под знаком предела разложить на множители, выполнить сокращение и вычислить предел)
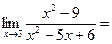
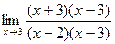 =
= 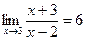
3.3 Пределы иррациональных функций (под знаком предела стоит один или несколько корней): числитель и знаменатель функции, стоящей под знаком предела умножить на выражение сопряженное знаменателю или числителю (и знаменателю и числителю), выполнить действия, сократить и вычислить предел.

2). 



3). 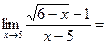
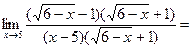


РАЗДЕЛ 1.2. Производная функции и ее геометрический смысл. Применение производной.
Формулы дифференцирования
| Производная элементарных функций | Производная сложных функций |
1. (lnx)' = 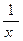 , ,
| (lnu)'=  , ,
|
2. (log  )' = )' =  , ,
| (log  )'= )'=  , ,
|
3. (lg  )' = )' =  , ,
| (lg  )'= )'= 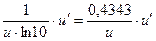 , ,
|
4. ( )' = )' = 
| ( )'= )'= 
|
5. ( )' = )' = 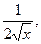
| ( )' = )' = 
|
6. ( )' = )' =  6* (ех)' = ех 6* (ех)' = ех
| (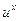 )' = )' =  (еu)' = еu ∙ u', (еu)' = еu ∙ u',
|
7. ( )' = cosx, )' = cosx,
| ( )' = cos )' = cos 
|
8. ( )' = - sinx, )' = - sinx,
| ( )' = - sin )' = - sin 
|
9. ( )' = )' =  , ,
| ( )' = )' =  , ,
|
10. ( )' = )' =  , ,
| (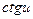 )' = )' =  , ,
|
11. ( )' = )' =  , ,
| ( )' = )' =  , ,
|
12. ( )' = - )' = -  , ,
| (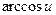 )' = - )' = -  , ,
|
13. ( )' = )' =  , ,
| ( )' = )' =  , ,
|
14. ( )' = – )' = –  , ,
| ( )' = - )' = -  , ,
|
15. 
| 
|
Правила дифференцирования
1) с' = 0, – производная постоянной функции,
2) х' = 1 – производная от х по аргументу х,
3) (u+v-w)' = u' + v' - w' – производная алгебраической суммы,
4) (u∙v)' = u'∙v + u∙v' – производная произведения
5) (c∙ u)' = c∙u' – постоянный множитель можно выносить за знак производной,
6)  – производная частного.
– производная частного.
Производные высших порядков
Пример:
Найти производную второго порядка от функции f(x)=x4.
Решение: f'(x)=(x4)' =4x3
f''(x)=(f'(x))'=(4x3)'=4=3x2=12x2 Ответ: f''(x)=12x2
Производная третьего порядка определяется аналогично - как производная от второй производной, т.е. все тоже последовательное дифференцирование. Например, третья производная от функции из предыдущего примера будет: f'''(x =24x
Дадим строгое определение производной старшего порядка:
Производной n-ого порядка f(n)(x) называется производная от производной (n-1)-го порядка.
Сложная функция и ее производная
Определение. Сложная функция - это функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = h (х), то у - cложная функция от х, то есть y = f (h (x)), определённой для тех значений х, для которых значения h (х) входят в множество определения функции f (u).
|
|
|
Например, если y=u2 и u=1+x3, то у - сложная функция от х, что можно записать следующим образом: y=(1+x3)2
В примере: у - сложная функция независимого аргумента х, а u - промежуточный аргумент.
Дифференцирование сложной функции (ТЕОРЕМА): Производная сложной функции равна производной по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной.
Коротко можно сказать так: Производная сложной функции равна произведению производных от функций, ее составляющих, т.е. 
Например:
Рассмотрим функцию y= (2x2- 1)3. Эту функцию можно рассматривать как сложную функцию, составленную из кубической функции y=f(u)=u3и квадратичной u=g(x)=2x2- 1. Тогда производная исходной функции находится следующим образом:
y=f(u)=u3, u=g(x)=2x2- 1.
y' = f '(u)∙u'(x) = (u3)'∙(2x2- 1)' = 3u2∙(2∙2x-0) = 3u2∙4x = 12u2x
 Вспомним, что функция u - промежуточная и введена нами для удобства нахождения производной от сложной функции, теперь нам надо вернуться обратно, подставив вместо этой промежуточной функции ее выражение: u=2x2- 1.
Вспомним, что функция u - промежуточная и введена нами для удобства нахождения производной от сложной функции, теперь нам надо вернуться обратно, подставив вместо этой промежуточной функции ее выражение: u=2x2- 1.
y'=12u∙x=12(2x2-1)=24x3-12x
Приложения производной.
5.1. Геометрический смыл производной:
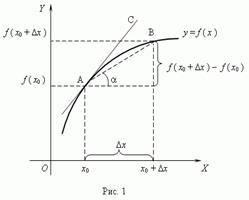
Рассмотрим график функции y = f (x).
Из рисунка 1 видно, что для любых двух точек A и B графика функции:  , где α - угол наклона секущей AB.
, где α - угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то  неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A, т.е.  . Отсюда следует: Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, т.е.
. Отсюда следует: Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, т.е. 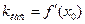 .
.
|
|
|


