 |
Уравнение касательной и нормали к графику функции
|
|
|
|
1. Касательной к графику функции в точке (х0; f(х0) называется предельное положение секущей (АС).
Уравнение касательной: y – f (x 0) = 
2. Прямая, перпендикулярная касательной (АС) в точке (х0; f(х0), называется нормалью к графику функции.
Уравнение нормали: y – f (x 0) = 
Задача: Составить уравнения касательной и нормали, проведённых к графику функции y=10x-x 
в точке с абсциссой равной х0=2.
Решение:
1. Находим ординату точки касания: f(х0)= f(2)=10∙2–22 =16,
2. Находим угловой коэффициент касательной: f'(х)= (10x-x )'=10-2х,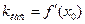 
= f' (2)=10–2∙2=6
3. Составляем уравнение касательной: y–16 = 6∙ (х-2), y–16 = 6х–12, y–6х–4 = 0 – уравнение касательной,
4. Составляем уравнение нормали: y –16 = 
, 6y –96 = –х+2, 6y+х–98=0 – уравнение нормали.
5.2. Физический смысл производной:
Определение. Скорость движения тела равна первой производной от пути по времени: 
Механический смысл производной:
Определение. Ускорение движения тела равно первой производной от скорости по времени или второй производной пути по времени: 
Задача: Определить скорость и ускорение точки, движущейся по закону 
в момент t=4c.
Решение:
1. Находим закон скорости: v= S'= 
2. Находим скорость в момент t = 4c: v (t)= v (4)=2∙42+8∙4=64 ед/сек
3. Находим закон ускорения: а=v′ =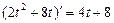 
4. Находим ускорение в момент t = 4c: а (t)= а( 4)=4∙4+8=24 ед/сек2
РАЗДЕЛ 1.3. Дифференциал функции и его применение в приближенных вычислениях. Понятие дифференциала функции
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х) ∙ ∆х (1).
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
|
|
|
Так как у'=х'=1, то, согласно формуле (1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (1) можно записать так: dy=ƒ'(х) ∙ dх (2)иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство dy/dx=ƒ'(х).
Пример1: Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).
Решение: По формуле dy=ƒ'(х) dx находимdy=(3х2-sin(l+2x))'dx=(6х-2cos(l+2х))dx.
Пример2: Найти дифференциал второго порядка функции: y = x3 –7x.
Решение: 
РАЗДЕЛ 1.4. Первообразная. Неопределенный интеграл. Способы вычисления неопределенного интеграла.
Определение1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке, дифференциал которой равен выражению f(x)dx. Пример: f(x) = 3х2 3х2dx F(x) = х3.
Однако дифференциалу функции соответствует не единственная первообразная, а множество их. Рассмотрим на примере: F1(x) = х3, F2(x) = х3 + 4, F3(x) = х3 - 2, в общем виде F(x) + С, где С - произвольная константа. Значит для функции f(x)= 3х2 существуют множество первообразных, отличающихся друг от друга постоянным слагаемым.
Определение2. Множество всех первообразных функций f(x) на некотором промежутке называется неопределённым интегралом от функций f(x) на этом промежутке и обозначается символом ∫f(x)dx.
Этот символ читается так: “интеграл от f(x) по dx”, таким образом по определению:
∫ (x)dx = F(x)+C.
Символ ∫ называется знаком интеграла, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования, F(x) - какая-либо первообразная,
С - постоянная.
Основные свойства неопределенного интеграла:
1. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.
d ∫ f(x)dx = f(x)dx.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной: ∫ d F(x) = F(x) + С
|
|
|
3. Постоянный множитель можно выносить за знак интеграла: ∫ kf(x)dx = k ∫ f(x)dx, k-const.
4. Неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от каждой из них: ∫ (f1(x)+f2(x)-f3(x))dx = ∫ f1(x)dx + ∫ f2(x)dx – ∫f3(x)dx.
|
|
|
