Пропускная способность канала связи

 

Введем определение пропускной способности канала связи в предположении, что сообщения источника и шумы, действующие в линии связи, носят эргодический характер.

Обозначив через Х_Т последовательность сообщений, создаваемых источником за время Т, ачерез W_Т соответ­ствующую ей последовательность принятых сообщений, определим количество информации I (W_T, Х_Т), содержащееся в последовательности сообщений W_T на выходе канала о последовательности X_Т наего входе. I (W_T,X_T)зависит от вероятностных характеристик источника сообщений и характеристик шумов, действующих в линии связи, метода кодирования сообщений, а также от промежутка времени Т.

Предел

(бит/с) (7.1)

определяет среднее количество информации, получаемое на выходе канала за единицу времени, и называется скоростью передачи информации.

При одном и том же способе кодирования длительность символов передаваемых сигналов может быть различной и зависит от вида модуляции и ширины полосы пропускания канала связи. С изменением длительности символов меняется и скорость передачи информации.

Положим, что нам известна некоторая совокупность фиксированных ограничений, накладываемых на информационный канал. К фиксированным ограничениям будем относить: параметры канала связи и, в частности, длительность передаваемых символов сигнала, используемый код, методы декодирования сигналов и накладываемые в связи с этим запреты и т.п.

Максимальную скорость передачи информации назовем пропускной способностью канала связи С:

. (7.2)

В данном равенстве обозначение Sup указывает, что вычисляется верхняя грань, а запись a _i Î B_i говорит о том, что параметр a _i удовлетворяет заданному фиксированному ограничению, т.е. лежит в некоторой области B_i.

 

При вычислении максимума скорости передачи могут представиться следующие случаи:

1) канал связи определен полностью: заданы способы кодирования и декодирования сообщений, длительностипередаваемых сигналов, полоса канала связии вероятностные характеристики помех; тогда максимальная скорость передачи информации отыскивается по статистическим характеристикам источника сообщений, т.е. разыскивают такое распределение вероятностей по сообщениям х,при котором скорость передачи информации наибольшая;

2) статистические показатели источника сообщений заданы;в этом случае способы модуляции, кодирования и декодирования выбираются так, чтобы скорость передачи информации была максимальной;

3) канал связи полностью не определен – имеется возможность изменять те или иные его параметры: дли­тельности символов, способ кодирования и т.п.; в этом случае параметры канала, которые не заданы, выбирают из условия получения возможно большей скорости пере­дачи информации, а максимум в (7.2) снова отыскивают по статистическим характеристикам источника сообще­ний.

Пропускная способность есть характеристика канала и не зависит от фактической скорости передачи информации от данного источника.

Пропускная способность линии связи определяется так

 

(бит/с), (7.3)

где

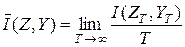. (7.3’)

При этом Z_T и Y_T – сигналы длительностью Т соответственно на выходе и входе канала связи.

Так как весь информационный канал связи не может про­пускать информацию со скоростью большей, чем его часть, то всегда С_С ³ С.

При отсутствии шумов w_Т = х_Т, z_Т = у_Т. На основании свойств количества информации

,

 

.

 

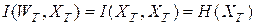Подставив последние выражения в (7.2) и (7.3), получим

 

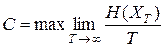, (7.4)

 

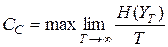. (7.5)

 

Обозначим через N (T)число всех возможных последова­тельностей сообщений, вырабатываемых источником, дли­тельностью Т. Энтропия Н (Х_Т)максимальна, если все эти последовательности равновероятны. Это максимальное значение равно log N (T), и выражения (7.4) и (7.5) можно переписать в виде

 

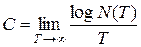, (7.6)

 

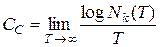, (7.7)

где N_k (T)– число всех возможных кодированных после­довательностей длительностью Т.

Соотношения (7.6) и (7.7) обычно используют в качестве определения пропускной способности дискретного канала без шумов.

Найдем пропускную способность некоторых дискретных каналов.

Пример 1. Пусть для передачи сообщений используется код с осно­ванием а (т.е. с а различными символами), длительность всех сим­волов кода одинакова и равна τ. Другие фиксированные ограничения отсутствуют.

Для вычисления С_C рассмотрим последовательность из М симво­лов. Длительность такой последовательности равна Т = M τ.При T → ¥число символов в одной последовательности M → ¥. Оче­видно, что всего можно образовать а^M последовательностей длиной в М символов, следовательно, N_C (М τ) = а^M и из (7.7) получим

или

. (7.8)

Нужно отметить, что если рассматривать выход кодирующего устройства как источник сообщений, то log а есть энтропия этого источника, т.е. log a = H (Y), у которого корреля­тивные связи между символами отсутствуют и вероятности передачи различных символов одинаковы. Отсюда следует и весьма важное обратное утверждение: для того чтобы в рассматриваемом ка­нале скорость передачи была максимальной, необходимо, чтобы вероятности передачи различных символов были одинаковыми.

При использовании двоичного кода а = 2из (7.8) получаем, что

дв.ед./сек. (7.9)

Для дискретных каналов принято обозначать , где V назы­вают скоростью передачи, которая выражается в бодах, если τ из­меряется в секундах. Таким образом, С_С = V, т.е. пропускная спо­собность двоичного канала А, выражаемая в двоичных единицах в секунду, равна скорости передачи в бодах.

Пример 2. В условиях предыдущей задачи нужно определить пропускную способность линии связи, если на допустимый вид кодовых последовательностей накладываются некоторые ограничения.

При вычислении С_с будем рассматривать кодирующее устройство как источник информации и используем результаты гл. 6.

Рассмотрим сигнал Y_T длительностью Т = Мτ. Энтропия этого сигнала

H (Y_T) = MH (Y),

где H (Y) – энтропия источника, вычисляемая с учетом наложенных фиксированных запретов.

Очевидно, что скорость передачи информации в таком канале

(7.10а)

а пропускная способность

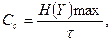(7.10б)

где H (Y)_max – максимально возможное значение энтропии кодированного сигнала с учетом наложенных запретов.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: