Кодирование как процесс выражения информации

В цифровом виде

Любому дискретному сообщению или знаку сообщения можно приписать какой-либо порядковый номер. Измерение аналоговой величины, выражающееся в сравнении ее с образцовыми мерами, также приводит к числовому представлению информации. Передача или хранение сообщений при этом сводится к передаче или хранению чисел. Числа можно выразить в какой-либо системе счисления. Таким образом, будет получен один из кодов, основанный на данной системе счисления.

Сравним системы счисления и построенные на их основе коды с позиций применения в системах передачи, хранения и преобразования информации.

Общепризнанным в настоящее время является позиционный принцип образования системы счисления. Значение каждого символа (цифры) зависит от его положения — позиции в ряду символов, представляющих число.

Единица каждого следующего разряда больше единицы предыдущего разряда в т раз, где т — основание системы счисления. Полное число получаем, суммируя значения по разрядам:

где i — номер разряда данного числа; l — количество разрядов; 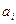— множитель, принимающий любые целочисленные значения в пределах от 0 до т — 1 и показывающий, сколько единиц i -гo разряда содержится в числе.

Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи.

Однако с ростом основания существенно повышаются требования к линии связи и аппаратуре создания и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.

Учитывая оба обстоятельства, целесообразно выбрать систему, обеспечивающую минимум произведения количества различных символов т на количество разрядов l для выражения любого числа. Этот минимум найден при воспроизведении определенного достаточно большого числа Q (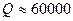). Определено, что наиболее эффективной системой является троичная []. Незначительно уступают ей двоичная и четверичная. Системы с основанием 10 и более существенно менее эффективны. Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты. выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе. Действительно, логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов сводится в этом случае к задаче обнаружения (есть импульс или нет импульса), что значительно проще.

Арифметические и логические действия также наиболее просто осуществляются в двоичной системе. В таблицы сложения, вычитания и умножения входит всего по четыре равенства:

Правила сложения:	Правила вычитания:	Правила умножения:
0 + 0 = 0	0 – 0 = 0	0 ∙ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ∙ 1 = 1

Наиболее распространенная при кодировании и декодировании логическая операция — сложение по модулю. В двоичной системе она также наиболее проста и определяется равенствами:

0 0 = 0	1 1 = 0
0 1 = 1	1 0 = 1

Алгоритм перевода из двоичной в привычную для человека десятичную систему несложен. Пересчет начинается со старшего разряда. Если в следующем разделе стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу.

Итак, для передачи и проведения логических и арифметических операций наиболее целесообразен двоичный код. Однако он неудобен при вводе и выводе информации, так как трудно оперировать с непривычными двоичными числами. Кроме того, запись таких чисел на бумаге оказывается слишком громоздкой. Поэтому, помимо двоичной, получили распространение системы, которые, с одной стороны, легко сводятся как к двоичной, так и к десятичной системе, а с другой стороны, дают более компактную запись. К таким системам относятся восьмеричная, шестнадцатеричная и двоично-десятичная. В восьмеричной системе для записи всех возможных чисел используется восемь цифр от 0 до 7 включительно. Перевод чисел из восьмеричной системы в двоичную крайне прост и сводится к замене каждой восьмеричной цифры равным ей трехразрядным числом. Например, для восьмеричного числа 754 получаем:

Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании.

Чтобы сохранить преимущества двоичной системы и удобство десятичной системы, используют двоично-десятичные коды. В таком коде каждую цифру десятичного числа записывают в виде четырехразрядного двоичного числа (тетрады). С помощью четырех разрядов можно образовать 16 различных комбинаций, из которых любые 10 могут составить двоично-десятичный код. Наиболее целесообразным является код 8-4-2-1 (табл. 7.1). Этот код относится к числу взвешенных кодов. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Двоично-десятичный код обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.

Таблица 7.1

Число в	Двоично-десятич-	Двоично-десятич-	Двоично-десятич-
Десятичном	ный код с весами	ный код с весами	ный код с весами
Коде	8-4-2-1	5-1-2-1	2-4-2-1
	0000 0000	0000 0000	0000 0000
	0000 0001	0000 0001	0000 0001
	0000 0010	0000 0010	0000 0010
	0000 0011	0000 0011	0000 0011
	0000 0100	0000 0111	0000 0100
	0000 0101	0000 1000	0000 1011
	0000 0110	0000 1001	0000 1100
	0000 0111	0000 1010	0000 1101
	0000 1000	0000 1011	0000 1110
	0000 1001	0000 1111	0000 1111
	0001 0000	0001 0000	0001 0000

Таблица 7.2

Число в	Код	Число в	Код	Число в	Код
десятичном	Грея	десятичном	Грея	десятичном	Грея
коде		коде		коде

В табл. 7.1 представлены два других двоично-десятичных кода с весами 5-1-2-1 и 2-4-2-1, которые широко используются при поразрядном уравновешивании в цифровых измерительных приборах.

Среди кодов, отходящих от систем счисления, большое практическое значение имеют такие, у которых при переходе от одного числа к другому изменение происходит только в одном разряде.

Наибольшее распространение получил код Грея, часто называемый циклическим или рефлекснд-двоичным. Код Грея используется в технике аналого-цифрового преобразования, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в табл. 7.2.

Правила перевода числа из кода Грея в обычный двоичный сводятся к следующему: первая единица со стороны старших разрядов остается без изменения, последующие цифры (0 и 1) остаются без изменения, если число единиц, им предшествующих, четно, инвертируются, если число единиц нечетно.

⇐ Предыдущая 1 234 5 Следующая ⇒

Воспользуйтесь поиском по сайту: