 |
Коррекция по ЛАЧХ эквивалентной разомкнутой структуры.
|
|
|
|
При проведении коррекции по ЛАЧХ эквивалентной разомкнутой структуры мы пользуемся понятиями исходная Lи и желаемая Lg ЛАЧХ. При выборе желаемой характеристики следует пользоваться следующими рекомендациями:
- Для обеспечения устойчивости частота среза должна располагаться на участке –20[дб/дек].
- Эта частота среза должна быть близкой, по возможности, к исходной частоте среза, т.к. значительное уменьшение частоты среза уменьшает полосу пропускания и следовательно увеличивает длительность переходного процесса, т.е. уменьшает быстродействие системы. Для упрощения расчётов желательно использование пассивного корректирующего звена, т.е. желаемая частота среза должна быть меньше исходной. (Пример расчёта активного корректирующего звена – см. [9 стр.148]).
- На низких частотах, чтобы не увеличивать погрешность в установившемся режиме и не усложнять реализацию корректирующего звена желаемая и исходная ЛАЧХ обычно совпадают. На высоких частотах для упрощения корректирующего звена также желательно совпадение желаемой и исходной ЛАЧХ.
- Для облегчения выбора параметров корректирующего звена надо, чтобы желаемая ЛАЧХ и ЛАЧХ корректирующего звена были близки к стандартным. Набор стандартных звеньев имеется почти во всех книгах по ТАУ, например [4].
Методика синтеза корректирующего последовательного звена.
1. Проводится построение ЛАЧХ исходной нескорректированной САУ в разомкнутом состоянии [Lи].
2. Проводится построение желаемой ЛАЧХ, обеспечивающей устойчивость и заданные показатели качества замкнутой САУ [Lg].
3. Вычисляется ЛАЧХ корректирующего звена как разность между ЛАЧХ желаемой и нескорректированной систем.
|
|
|
4. По виду Lkиз таблиц корректирующих звеньев выбираем звено с соответствующей характеристикой, В случае если расчетное звено имеет сложную зависимость Lk, то его нужно разбить на простые, которые имеются в таблицах корректирующих звеньев, и набирать его путем стыковки элементарных звеньев.
Пример коррекции по ЛАЧХ эквивалентной разомкнутой структуры:
Пусть передаточная функция разомкнутой структуры равна:
Путем коррекции необходимо обеспечить:
tп≤1,5 с; σ%=30%.
График ЛАЧХ соответствующий WР в асимптотическом приближении дан на рис. 8.
Рис.8
Корректирующее звено включено последовательно, поэтому 
Частоту среза желаемой ЛАЧХ можно определить по зависимости [9]:
где: tp - время переходного процесса;
b - коэффициент, связанный с перерегулированием s. Эта связь показана в табл.1.
Таблица 1.
| s % | ||||
| b | 1.7 | 2.2 | 3.0 | 4.0 |
Через рассчитанную и отмеченную на оси частот точку wсрg проводим среднечастотную асимптоту желаемой ЛАЧХ с наклоном –20[дб/дек], Среднечастотную асимптоту ограничивают со стороны низких частот значением частоты 
. Здесь w в - значение частоты, ограничивающей среднечастотный участок желаемой ЛАЧХ со стороны области высоких частот и определяется по зависимости 
. Выполнение этих условий обеспечивает ширину среднечастотного участка желаемой ЛАЧХ в пределах (0,9‑1,1) дек в логарифмической системе координат и гарантирует устойчивость и требуемое качество переходного процесса.
Для нашего примера частоты равны:
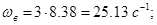
В приведённом примере корректирующее звено состоит только из одного простого пассивного звена, имеющего следующую ЛАЧХ. (рис 9):
На рис.7 приведена схема данного корректирующего звена, параметры которого могут быть выбраны по следующим формулам:
L
Т3-1 Т1-1 Т2-1 Т4-1
ω
- 20 +20
- 20lga
Рис.9
Рассчитаем 
:
|
|
|
Т.о. корректирующее звено для нашей системы будет иметь вид:
Рекомендуемая литература:
1. Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического управления техническими системами. Учеб. Пособие М.. Изд-во МГТУ, 1993, 492 с
2. Сабинин А.Н. Электромашинные устройства автоматики. Л., Энергоатомиздат. 1988г.
3. Теория автоматического управления: Учебное пособие для вузов ч.I. Теория линейных систем автоматического управления. Под ред. А.А. Воронова. М, Высшая школа, 1977, 303 с.
4. Бесекерский В.А., Попов Е.П., Теория систем автоматического регулирования. М., Наука, 1975, 768 с.
5. Удерман Э.Г. Метод корневого годографа в теории автоматических систем. М., Наука, 1972 г., 448 с.
6. Курс лекций по теории управления Либерзон К.Ш., Сам ГТУ, 2000-2001 г.г.
7. Дьяконов В.П. Система MathCAD. Справочник. Радио и связь. 1993г., 128 с.
8. Куропаткин П.В. Теория автоматического управления. М., Высшая школа,1973, 527с
9. Лысов В. Е. Теория автоматического управления. Основы линейной теории автоматического управления. Самара, СамГТУ, 2001. 200с.
|
|
|
