Задачи для самостоятельной работы

Основная

 

1. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей.-Л.: Энергия, 1972.-с. 137-152.

2. Гуревич И.В. Основы расчетов радиотехнических цепей.-М.: Связь, 1975.- с.60-71.

3. Попов В.П. Основы теории цепей.-М.: Высш.шк.,1985.-с.158-175.

4. Попов В.П. Основы теории цепей.-М.:Высш.шк.,2000.-с.177-198.

 

Дополнительная

 

1. Гольдин О.Е. Задачник по теории электрических цепей.-М.: Высш. школа, 1969.-с. 45-48.

2. Шебес М.Р. Теория линейных электрических цепей в упражнениях и задачах.-М.: Высш.школа,1973.-с.137-139, 144-153.

3. Жуков В.П., Карташев В.Г., Николаев А.М. Сборник задач по курсу “Радиотехнические цепи и сигналы”.-М.: Сов.радио,1972.-с.31-33.

4. Сборник задач по теории электрических цепей./Под ред. Матханова П.Н. и Даниловой Л.В.-М.: Высш.школа,1980.-с.156.

 

ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

Цель занятия

 

Усвоить основные соотношения и характеристики простых и сложных параллельных контуров; научиться сравнительному анализу последовательного и параллельного контуров.

 

Краткие теоретические сведения

 

Для параллельного контура любого вида (рисунок 6.1) входное сопротивление на всех частотах, для которых выполняется условие

 

| Х₁ | >> R₁ и | Х₂ | >> R₂ (6.1)

 

определяется как

 

, (6.2)

 

 

а) обобщенная схема параллельного контура

б) простой контур I вида

в) сложный параллельный контур с разделенными индуктивностями

или контур II вида

г) сложный параллельный контур с разделенными емкостями или

контур III вида.

 

В контурах с добротностью Q ³ 5, для которых | X_1р | » R₁ и | X_2р | » R₂, условие (5.1) имеет вид

 

X_1р + X_2р = 0,

 

что определяет частоту резонанса токов как

 

 

а резонансное сопротивление, в соответствии с формулами (5.2) и (6.2), как

R_р »

 

где L, C, R - полные параметры контуров, определяемые при “последовательном” обходе любого из контуров на рисунке 6.1:

 

R = R₁ + R₂, L = L₁ +L₂ , C= .

Добротность контура любого вида

 

Q =

 

Для простого параллельного контура

 

.

 

Для сложных параллельных контуров

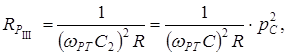где

 

где

 

 

Если полные параметры L, C, R простого и сложного контуров одинаковы, то

 

R_{р сл} = p² × R_{p I},

 

где р < 1 и соответственно р = для II вида и р = для III вида.

В простом контуре (см.рисунок 6.1б) на частоте резонанса

 

, (6.3)

 

где - ток в неразветвленной ветви, т.е. входной ток контура,

- ток внутри контура.

Соотношение (6.3) и обусловило название резонанса в параллельном контуре как резонанса токов.

На частотах, отличных от резонансных, любой из контуров представляет собой комплексное сопротивление

 

.

 

Частотные характеристики простого параллельного контура при соблюдении условия (6.1):

(6.4)

,

 

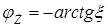
Частотные характеристики сложных параллельных контуров в области определяются также выражениями (6.4), при условии, что R_р -резонансное сопротивление сложного контура. В целом частотные характеристики простого и сложных контуров существенно отличаются, т.к. для последних имеют место и резонанс токов и резонанс напряжений.

Резонанс напряжений имеет место в ветвях, содержащих последовательно включенные L и С:

 

и

 

для контура II и III вида соответственно (см. рисунок 6.1).

Мощность, выделяемая в контуре любого вида, на частоте

 

или

.

Если контур питается от генератора напряжения (тока) с внутренним сопротивлением R_i, то в контуре любого вида выделяется максимально возможная для данного источника сигнала мощность при условии

 

R_p = .

 

Шунтирующее сопротивление R_ш (а таковым является также и внутреннее сопротивление генератора R_i) всегда увеличивает сопротивление потерь контура, снижает его добротность, увеличивает полосу пропускания. Добротность шунтированного контура.

где R_доп» 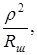если R_ш >> .

Задачи для самостоятельной работы

 

Задачи этого раздела используются для самостоятельной работы в аудитории и индивидуальных домашних заданий. Наиболее простыми являются задачи 6.3.1-6.3.13.

6.3.1 Найти сопротивление простого параллельного контура при резонансе по следующим данным:

 

№	Q	R, Ом	L, мкГн	С, пФ	r, Ом	fр,кГц	2Dfп,кГц
			-	-	-	-	-
	-		-	-		-	-
	-				-		-
	-		2×103		-		-
			-		-		-
	-				-	-	-
			-	-	-	-	-
	-		-	-		-	-
	-		-	-	-

 

6.3.2 Определить, как следует распределить индуктивности или емкости сложного параллельного контура между его ветвями, чтобы его резонансное сопротивление было равно заданному. Расчеты произвести по данным таблицы, где L, C, R - полные параметры контуров

 

№	L, мкГн	С, пФ	R, Ом	Rр, кОм

 

6.3.3. По данным таблицы вычислить активную составляющую, реактивную составляющую и модуль сопротивления простого параллельного контура на частоте f, не равной f_р; Df - абсолютная расстройка контура.

 

№	f, МГц	L, мкГн	С, пФ	R, Ом	Df, кГц	Q	fP , МГц
	-				-5	-	-
	0,305	-		-	-		0,3
	0,964		-	-	-		0,96
	0,255	-			-	-	0,25
					-6		0,4

 

6.3.4. Простой параллельный контур имеет добротность Q =80, сопротивление потерь 20 Ом, полосу пропускания 2·10⁴рад/с. Как изменится полоса пропускания контура при подключении к нему шунтирующего сопротивления 50 кОм?

Ответ: 7×10⁴рад/с.

 

6.3.5. Контур (см.рисунок 6.1г) имеет следующие параметры: С₁=С₂ =300 пФ, R₁ =5 Ом, R₂ =0, L =300 мкГн. К нему подключено шунтирующее сопротивление R_ш =5 кОм. Найти частоты последовательного и параллельного резонансов; вычислить резонансное сопротивление и полосу пропускания с учетом R_ш.

Ответ: 0,333×10⁷ рад/с; 4,72×10⁶ рад/с; 4,76 кОм;0,35×10⁵ рад/с.

 

6.3.6. Определить входное сопротивление двухполюсников (рисунок 6.2), если сопротивления отдельных участков цепи на схеме указаны в омах.

Ответ: 16,01 кОм; 50,005 кОм; 8,02 кОм; 40,1 кОм.

 

6.3.7. Для параллельных контуров на схемах рисунка 6.2а,в вычислить добротность Q, характеристическое сопротивление r и коэффициент включения индуктивности или емкости _.

Ответ: а) 60; 600; 0,66(6); в) 45; 900; 0,44(4).

 

 

6.3.8. В простом параллельном контуре высокой добротности L =144 мкГн, С =400 пФ. Мощность, потребляемая контуром при резонансе, равна 50 мВт, амплитуда напряжения на емкостном элементе U_сm =60 В. Определить сопротивление потерь, добротность контура и полосу пропускания.

Ответ: 10 Ом; 60; 6,95×10⁴ рад/с.

 

6.3.9. Простой параллельный контур подключен к генератору напряжения с внутренним сопротивлением 50 кОм. Параметры контура: С =500 пФ, Q =100, w_р = 10⁶рад/с. Определить эквивалентную добротность и полосу пропускания.

Ответ: 20; 5×10⁴рад/с.

 

6.3.10. Генератор с частотой 320 кГц, амплитудой 100 В и внутренним сопротивлением 1 кОм подключен к простому параллельному контуру, настроенному в резонанс с частотой генератора. Индуктивность контура L =100 мкГн, добротность Q = 100. Определить мощность, выделяющуюся в контуре.

Ответ: 226 мВт.

 

6.3.11.Контур (см.рисунок 6.1г) имеет следующие параметры: L =2,7 мкГн, С₁= 80 пФ, С₂ =50 пФ, R =9 Ом. Амплитуда тока в неразветвленной части схемы 10 мА. Определить резонансную частоту параллельного контура, его резонансное сопротивление и найти мощность, выделяемую на контуре при резонансе.

Ответ: 17,5 МГц; 3,65 кОм; 0,182 Вт.

 

6.3.12. На частоте 4,5 МГц параллельный контур должен иметь чисто активное входное сопротивление, равное 10 кОм. Как следует включить параллельный контур, обладающий требуемой резонансной частотой, емкостью 150 пФ и добротностью 100, чтобы удовлетворить поставленному условию?

Ответ: p = 0,652.

 

6.3.13. Индуктивность катушки параллельного контура равна 1 мГн, сопротивление потерь контура определяется потерями в катушке и равно 10 Ом. Рассчитать контур так, чтобы на частоте 10⁶рад/с его сопротивление было активным и равным 25 кОм.

Ответ: 1000 пФ; p =0,5.

 

6.3.14. Контур (см.рисунок 6.1г) имеет параметры: R =5 Ом, L =150мкГн, полная емкость С =500 пФ, R_p= 20 кОм. Определить емкости С₁ и С₂. Как надо включить элементы этой схемы, чтобы входное сопротивление на резонансной частоте было максимально возможным? Вычислить его значение.

Ответ: 1183 пФ; 866 пФ; 60 кОм.

 

6.3.15. Простой параллельный колебательный контур, имеющий Q =100, подключили к генератору с амплитудой Е_m = 4 B и внутренним сопротивлением Ri = 20 кОм. При какой величине сопротивления потерь R в контуре выделяется максимальная мощность Р_{к mах}? Чему она равна? Какова относительная полоса пропускания контура при подключении его к генератору?

Ответ: 2 Ом; 0,1 мВт; 0,02.

 

6.3.16. Контур II вида (см.рисунок 6.1в)имеет параметры R₁=R₂ = =5 Ом, L₂ = 500 мкГн, С =1000 пФ; он подключен к генератору напряжения с внутренним сопротивлением 10 кОм и Е =10 В. Какая мощность выделяется на контуре в момент резонанса токов, если известно, что резонанс напряжений наступает на частоте =10⁶ рад/с?

Ответ: 2,34 мВт.

 

6.3.17. Простой параллельный контур с параметрами L= 200 мкГн, С= 400 пФ, R= 10 Ом подключен к генератору напряжения с внутренним сопротивлением R_i =30 кОм и э.д.с. е(t)= 200 coswt B. Найти напряжение на контуре , ток 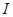вне контура, контурный ток , а также мощность, выделяемую в контуре при резонансе и на частоте f = 1,01 f_р.

Ответ: 125 В; 2,5 мА; 176,8 мА; 156,25 мВт; 135,65 мВт.

 

6.3.18. Контур с разделенными индуктивностями (см.рисунок 6.1в) настроен на длину волны l= 60 м и имеет на этой частоте резонансное сопротивление 16 кОм, емкость контура 100 пФ, сопротивление потерь 4 Ома. Определить L₁ и L_{2 .}

Ответ: 2 мкГн; 8 мкГн.

 

6.3.19. Контур с двумя емкостями настроен на длину волны l= 100 м, имеет R_рIII = 40 кОм; его добротность Q =100, L =30 мкГн. Определить С₁, С₂ и сопротивление потерь.

Ответ: 585 пФ; 112 пФ; 5,65 Ом.

 

6.3.20. Амплитуда напряжения на параллельном контуре (см.рисунок 6.1б) 2 кВ, действующее значение тока в контуре 5 А, мощность, выделяемая в контуре, 450 Вт. Определить параметры контура, если резонансная частота его 6 МГц.

Ответ: 18 Ом; 93,5 пФ; 7,5 мкГн.

 

6.3.21. Известно, что на резонансной частоте 0,5 МГц в простом параллельном контуре выделяется мощность 500 Вт, при этом амплитуда напряжения на контуре 3 кВ, а действующее значение тока в контуре 5 А. Определить L, C, R.

Ответ: 135 мкГн; 750 пФ; 20 Ом.

 

6.3.22. Рассчитать простой параллельный контур так, чтобы на частоте 10⁷ рад/с его сопротивление было активным и равным 14 кОм, а на частоте 1,07×10⁷ рад/с модуль полного сопротивления контура был равен 1 кОм.

Ответ: 14 мкГн; 715 пФ; 1,4 Ом.

 

6.3.23. Простой параллельный контур настроен на длину волны 400 м. Индуктивность контура 200 мкГн, сопротивление потерь 10 Ом. На какой частоте реактивная составляющая сопротивления контура имеет максимальное значение и емкостной характер?

Ответ: 754 кГц.

 

6.3.24. Через неразветвленную цепь простого параллельного контура протекает ток i(t) =100+2 cosw_рt +50 cos 2 w_рt +10 cos 3 w_pt мА. Параметры контура: L= 50 мкГн, С =200 пФ, R =5 Ом. Определить напряжение на контуре и(t).

Ответ: 0,5+100 cosw_рt +16,7 cos (2 w_рt- 89,6⁰) + 1,88 cos (3 w_рt - 89,8⁰) В.

 

6.3.25. Сложный параллельный контур (см.рисунок 6.1в) подключен к генератору с внутренним сопротивлением 100 кОм. Параметры контура: С =500 пФ, L₂ =500 мкГн, Q =100, =10⁶ рад/с. Определить эквивалентную добротность и полосу пропускания.

Ответ: 88,9; 11 250 рад/с.

 

6.3.26. Простой параллельный контур подключен к генератору с внутренним сопротивлением = 15 кОм и амплитудой Е_m = 5 В. Схема должна быть настроена на частоту 300 кГц, иметь полосу пропускания 6 кГц (с учетом влияния генератора); кроме того, в контуре должна выделяться максимальная мощность. Найти параметры контура L, C, R. Вычислить мощность в контуре на резонансной частоте.

Ответ: 80 мкГн; 3520 пФ; 1,5 Ом; 1,875 мВт.

 

6.3.27. Изобразить схему контура, рассчитать его параметры и резонансное сопротивление, если известно, что частота параллельного резонанса 600 кГц, а частота последовательного резонанса 400 кГц. Добротность контура на частоте параллельного резонанса равна 100, полное сопротивление потерь 5 Ом.

Ответ: 132,7 мкГн; 530,7 пФ; 15,42 кОм.

 

6.3.28. Параллельный контур должен быть настроен на частоту 600 кГц, иметь резонансное сопротивление 10 кОм и полосу пропускания 2 кГц. Кроме того, контур должен обеспечить подавление второй гармоники (1,2 МГц). Изобразить схему контура и определить его параметры.

Ответ: 15,73 мкГн; 4480 пФ; 0,2 Ом.

 

6.3.29. Изобразить схему и рассчитать параметры параллельного контура так, чтобы на частотах 1,6 и 4 МГц его сопротивление было активным и соответственно равным 5 Ом и 10 кОм. Сопротивление потерь контура равно 10 Ом. Каков характер реактивной составляющей сопротивления контура на частоте 1,59 и 4,04 МГц?

Ответ: 15 мкГн; 105,8 пФ.

 

6.3.30. Изобразить схему, рассчитать параметры и резонансное сопротивление параллельного контура, если известно, что частота параллельного резонанса должна быть равной 700 кГц, частота последовательного резонанса 500 кГц, добротность 150, сопротивление потерь 4 Ом.

Указание: выразите полосу пропускания через параметры R и L.

Ответ: 136 мкГн; 379 пФ; 21,6 кОм.

 

6.3.31. Сложный параллельный контур настроен на частоту 25 МГц. При этом параметры контура выбраны так, что правая ветвь контура оказалась настроенной на частоту 50 МГц. Изобразить схему и определить параметры контура, если сопротивление потерь 10 Ом, а резонансное сопротивление = 18 кОм.

Ответ: 3,6 мкГн; 11,1 пФ.

 

6.3.32. Изобразить схему и рассчитать параметры сложного параллельного контура, который на частоте 10⁷ рад/с должен обладать активным сопротивлением, равным 10 кОм, а на частоте 2×10⁷ рад/с - активным сопротивлением 10 Ом. Полное сопротивление потерь контура 20 Ом.

Ответ: 59,6 мкГн; 168 пФ; 10 Ом.

 

6.3.33. На входе сложного параллельного контура действует источник тока i(t)= 2×10^-3 cos 10⁶ t +2×10^-3 cos 2×10⁶ t А. Индуктивность контура L =500 мкГн. Определить структуру и параметры контура таким образом, чтобы напряжение на нем было u(t)= 15 ×10^-3 cos 10⁶ t +75 cos 2×10⁶ t B.

Ответ: 500 пФ; 15 Ом (полное).

 

6.3.34. Параллельный контур должен обеспечить подавление первой гармоники колебания, имеющей частоту 25 МГц, а на второй гармонике иметь резонансное сопротивление 10 кОм и полосу пропускания 500 кГц. Изобразить схему контура и определить его параметры.

Ответ: 0,567 мкГн; 18 пФ; 1,8 Ом.

 

6.3.35. Параметры простого параллельного контура: L= 17 мкГн, С = 248 пФ, R =16 Ом. Вычислите: 1) какой должна быть амплитуда напряжения на контуре, чтобы мощность, выделяемая в контуре при резонансе, была 150 Вт; 2) при каком и Е_m генератора напряжения эта мощность является максимально возможной; 3) мощность, выделяемую в контуре, подключенном к генератору с найденными параметрами Е_m и на граничных частотах полосы пропускания не шунтированного контура; во сколько раз она меньше максимально возможной мощности?

Ответ: 1133 В; 4,28 кОм; 2266 В; 120 Вт; 1,25.

 

6.3.36. Параллельный контур состоит из катушки L =400 мкГн, R_L =18 Ом и конденсатора С = 400 пФ, R_C =2 Ом. Контур подключен к генератору гармонических колебаний с амплитудой Е_m =200 В и внутренним сопротивлением 10 кОм. Как нужно подключить контур к генератору (как простой? как сложный с коэффициентом включения р?), чтобы в нем выделялась максимальная мощность. Определить эту мощность. Определить полосу пропускания контура, подключенного к генератору.

Ответ: р = 0,445; 0,5 Вт; 10⁵ рад/с.

 

Примечание: в задачах 6.3.27-6.3.34 в ответах указаны полные значения L и С, чтобы ответ не являлся подсказкой о типе сложного контура, однако студент должен определить L₁ и L₂ для II вида и С₁, С₂ для III вида контура.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: