 |
Тема 1.2 Принцип программного управления
|
|
|
|
Тема 1. 2 Принцип программного управления
1. Основные положения принципа программного управления
Современные ЭВМ строятся на одном принципе – принципе программного управления. В основе принципа программного управления лежит представление алгоритма в форме операторной схемы, которая задает правило вычислений, как композицию операторов ( операций над информацией) двух типов: операторов, обеспечивающих преобразование информации, и операторов, анализирующих информацию с целью определения порядка выполнения операторов. Реализация этого принципа в различных ЭВМ может быть разной. Используемый в современных компьютерах принцип программного управления был предложен в 1945 году Дж. фон Нейманом [2], и с тех пор неймановский принцип программного управления используется в качестве основного принципа построения ЭВМ. Этот принцип включает следующие положения.
1. Информация кодируется в двоичной форме и разделяется на единицы (элементы) информации, называемые словами.
2. Разнотипные слова информации (числа, символы, команды) различаются по способу использования, но не способами кодирования.
3. Слова информации размещаются в ячейках памяти машины и идентифицируются номерами ячеек, называемыми адресами слов.
4. Алгоритм представляется в форме последовательности управляющих слов, которые определяют наименование операции и слова информации, участвующие в операции, и называются командами. Алгоритм, представленный в терминах машинных команд, называется программой.
5. Выполнение вычислений, предписанных алгоритмом, сводится к последовательному выполнению команд в порядке, однозначно определяемом алгоритмом.
|
|
|
Дадим некоторые короткие комментарии перечисленных положений принципа программного управления.
Использование в ЭВМ двоичных кодов обусловлено спецификой электронных схем, применяемых для передачи, хранения и преобразования информации. Совокупности битов информации, используемых для представления отдельных чисел, команд и т. п., рассматриваются как самостоятельные информационные объекты и называются словами. Слово обрабатывается в ЭВМ как одно целое - как машинный элемент информации.
Согласно второму положению, все слова в ЭВМ выглядят совершенно одинаково и сами по себе неразличимы. Только порядок использования слов в программе вносит в них различия. Благодаря такому ‘однообразию’ слов оказывается возможным использовать одни и те же операции для обработки слов различной природы, например, и чисел, и команд.
Третье положение фиксирует специфику хранения и идентификации (обозначения) информации, порождаемую свойствами машинной памяти. Машинная память - совокупность ячеек, каждая из которых служит местом для хранения слова информации, и наиболее подходящий синоним этого термина - ‘склад информации’. Ячейка памяти выделяется для хранения значения величины, в частности, константы или команды. Чтобы записать слово в память, необходимо указать адрес ячейки, отведенной для хранения соответствующей величины. Чтобы выбрать слово из памяти (прочитать его), следует опять же указать адрес ячейки памяти. Таким образом, адрес ячейки становится машинным идентификатором (именем) величины и команды. Для обозначения величин и команд в ЭВМ нет никаких других средств, кроме адресов, присваиваемых величинам и командам в процессе составления программы вычислений. Кроме того, отметим, что выборка (чтение) слова из памяти не разрушает информацию, хранимую в ячейке. Это позволяет любое слово, записанное однажды, читать какое угодно число раз, т. е. из памяти выбираются не слова, а копии слов. Дополнительно к сказанному следует заметить, что адрес ячейки может быть представлен в ЭВМ как и любое другое слово информации, что используется в операциях индексирования и базирования.
|
|
|
В четвертом положении принципа программного управления утверждается, что программа представляется в ЭВМ в виде упорядоченной линейной последовательности команд следующего вида:
1 r 1 m 1 m 1 m 1 m 1 m
| КО | А 
| А 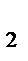
| ... | ... | А 
|
Здесь прямоугольник обозначает слово информации, части которого, имеющие определенный смысл, принято называть полями. Так, КО, А  , А
, А 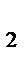 , ... , А
, ... , А  - поля команды, представляющие соответственно код операции и адреса операндов, участвующих в операции. Сверху указаны номера двоичных разрядов полей: код операции состоит из r битов, каждое поле адреса операнда А
- поля команды, представляющие соответственно код операции и адреса операндов, участвующих в операции. Сверху указаны номера двоичных разрядов полей: код операции состоит из r битов, каждое поле адреса операнда А  - А
- А  содержит m битов. Приведенное представление команды характеризует структуру или, иначе, формат команды.
содержит m битов. Приведенное представление команды характеризует структуру или, иначе, формат команды.
Согласно пятому положению, память неймановской машины сугубо линейна. Это выражается в том, что процесс вычислений, выполняемых ЭВМ по заданной программе, начинается с команды, заданной пусковым адресом программы. За ней выполняется следующая в памяти команда. Последовательность нарушается только в том случае, если выполняется команда условного или безусловного перехода, в которой непосредственно указывается адрес следующей команды. Процесс вычислений продолжается до тех пор, пока не будет выполнена команда, предписывающая прекращение вычислений.
Неймановский принцип программного управления не является единственно возможным принципом функциональной организации ЭВМ. Так, Дж. Айлиф в [3 ] предлагает принципы построения машины, отличной от традиционных неймановских машин. Отличия сводятся в основном к следующему.
Во-первых, предлагается тип информации отображать в кодах данных (сравни с п. 2). В результате числа, адреса, команды окажутся различимыми в программе и операция, указываемая в команде, производится машиной в форме, соответствующей типам операндов, что должно уменьшить число потенциальных ошибок в программе.
|
|
|
Во-вторых, вследствие линейности памяти ЭВМ ( см. пояснения к п. 5), программист вынужден любую структуру данных (вектор, матрицу, таблицу) спроектировать на линейную цепочку адресов I, I+1, ...... I+N. Затем при обработке информации из структуры данных, приходится выделять адреса отдельных структурных элементов. Процедуры размещения в памяти и выделения из нее отдельных элементов достаточно сложны. Дж. Айтлиф предлагает вносить описание структуры данных непосредственно в память машины и за счет этого обеспечить автоматическое выявление адресов отдельных элементов в процессе выполнения программы, что также должно уменьшить число потенциальных ошибок программиста.
Очевидно, что дополнительные возможности ЭВМ обеспечиваются за счет введения дополнительной аппаратуры и ее усложнения, а следовательно, и повышения стоимости. К настоящему времени принципы Айтлифа не нашли воплощения в продукции каких-либо известных компьютерных фирм. Неоднократно декларируется необходимость пересмотра неймановского принципа, так как возможности таких машин доведены до предела. Однако и в параллельных и конвейерных ЭВМ процессоры работают по принципу Дж. фон Неймана, что является убедительным подтверждением того, что этот принцип является наиболее рациональным принципом построения ЭВМ.
Тема 1. 3 Формы представления чисел в ЭВМ.
1. Система счисления
2. Правила перевода чисел из одной системы счисления в другую
3. Представление чисел с фиксированной и плавающей точкой
В точных науках известны позиционная и непозиционная системы счисления.
1. Система счисления (СС) - способ наименования и изображения чисел с помощью символов, имеющих определенное количественное значение.
В непозиционной системе счисления цифры не меняют своего количественного значения в зависимости от расположения в изображении числа. Так, непозиционное римское Х имеет значение " десять" в числе XXX -тридцать, и в числе LX- шестьдесят. Непозиционные системы счисления не получили широкого распространения из-за громоздкости изображений и сложных правил получения значений по изображению.
|
|
|
В позиционной СС количественное значение каждой цифры зависит от ее места (позиции) в числе. Количество (Р) различных цифр, используемых для изображения числа в позиционной СС, называется основанием СС. Значения цифр лежат в диапазоне от 0 до (Р-1).
В общем случае запись любого смешанного числа в СС с основанием Р будет представляться в виде ряда:
 (1)
(1)
Нижние индексы определяют местоположение цифры в числе (разряд):
- положительные значения индексов, включая нуль — для целой части числа (m разрядов);
- отрицательные значения - для дробной части числа (s разрядов).
Максимальное целое число, которое может быть представлено в m разрядах:

 (2)
(2)
Минимальное значение, не равное 0, которое можно записать в s разрядах дробной части, равно 
 (3)
(3)
В общем случае, имея Р разрядов целой части числа и S - дробной, можно записать  разных чисел. Именно это выражение представляет диапазон отображаемых значений.
разных чисел. Именно это выражение представляет диапазон отображаемых значений.
ЭВМ оперирует с числами, содержащими конечное число разрядов. Количество разрядов ограничено длиной разрядной сетки машины, под которой понимается совокупность битов информации, предназначенных для хранения и обработки машинных слов. Как следует из вышеизложенного, диапазон представления чисел в ЭВМ ограничен размерами машинных слов.
Двоичная система счисления имеет основание Р=2 и использует для представления информации всего 2 цифры - 0 и 1. Существуют правила перевода чисел из одной системы счисления в другую, основанные на соотношении (1). Например, двоичное число 101110, 101 равно десятичному
46, 625:
101110, 101 =1*25+0*24+1*23+1*22+1*2'+0*2°+1*2-1+0*2-2+1*2-3= 32 + 8 + 4 + 2 + 0, 5 + 0, 125 = 46, 625
2. Правило перевода из двоичной СС в десятичную: определить вес каждого двоичного разряда в десятичной СС и сложив значения весов с единичными значениями разрядов (не забывайте, что абсолютные значения весов увеличиваются справа - налево в целой части и слева - направо - в дробной).
Перевод десятичного числа в СС с другим основанием непосредственно по соотношению (1) для человека весьма затруднителен, т. к. все действия, предусмотренные этим соотношением, необходимо выполнять в той СС, в которую переводится число. Однако, можно воспользоваться соотношением (1) и сделать перевод проще, если преобразовать отдельно целую и дробную части выражения (1) к виду:
((…( 

Алгоритм перевода числа из десятичной СС в систему счисления с основанием р, основанный на этих выражениях, позволяет оперировать с числами в десятичной СС (той СС, из которой число переводится) и предусматривает отдельный перевод целой и дробной частей:
|
|
|
- для перевода целой части числа, исходное число, а затем и целые части, получающиеся в процессе преобразований, следует последовательно делить на основание р до тех пор, пока целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево (от последних к первым), образуют целую часть числа в СС с основанием р;
- для перевода дробной части исходное число, а затем дробные части, получающиеся в процессе преобразований, следует последовательно умножать на основание р до тех пор, пока очередная дробная часть произведения не окажется равной 0 ( число переводится в новую СС точно) или не будет достигнута заданная точность (после s произведений дробная часть не равна 0 - число переводится в новую СС неточно). Целые части произведений, записанные после запятой последовательно слева направо (в порядке получения, от первых к последним) образуют дробную часть числа в СС с основанием р. Согласно вышеизложенным правилам, перевод в двоичную систему числа 46, 625 будет следующим:
целая часть 46; процесс деления: 1) 46: 2=23 (остаток 0), 23: 2=11 (остаток 1), 11: 2=5 (остаток 1), 5: 2=2 (остаток 1), 2: 2==1 (остаток 0), 1: 2=0 (остаток 1). Итог: записываем остатки в обратном порядке:
101110;
дробная часть: 0, 625; процесс умножения: 1) 0, 625*2+1, 250 (целая часть 1), 0, 25*2=0. 5 (целая часть 0), 0, 5*2=1, 0 (целая часть 1). Итог:
записываем целые части в порядке получения: 101.
Дампы памяти (распечатки содержания ячеек программы) представляются в шестнадцатеричной СС. Перевод из десятичной системы счисления в шестнадцатеричную осуществляются по следующему правилу: каждая цифра шестнадцатеричного числа представляется четырьмя разрядами двоичного по таблице
| Десятичное число | Двоичное число | Шестнадцатеричное число |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
Чтобы количество разрядов было кратно 4, можно добавлять незначащие нули слева к целой части числа и справа – к дробной. Используя изложенные выше положения, можнозаписать равенство:
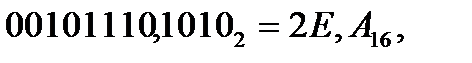
здесь нижние индексы указывают СС, в которой представляется число.
3. Представление чисел с фиксированной и плавающей точкой
Для представления в ЭВМ используются 2 формы: естественная (с фиксированной точкой) и нормальная ( с плавающей точкой).
Естественная форма представления предполагает, что положение запятой, отделяющей целую часть числа от его дробной части фиксировано в разрядной сетке ЭВМ. Кроме того, эти числа могут быть беззнаковыми (положительными) или иметь знак, для представления которого выделяется специальный разряд – знаковый. Как правило, это самый старший разряд в числе (крайний левый). Для положительных чисел в знак. Разряд заносится – 0, для отрицательных – 1. В ЭВМ известны 2 способа фиксирования положения запятой – либо перед старшим разрядом числа (после знакового разряда, если он имеется), либо после младшего разряда. Разрядная сетка ЭВМ для этих вариантов может быть представлена так, как показано на приведенных ниже иллюстрациях (в прямоугольниках, показывающих разряды двоичных чисел, проставлены веса разрядов).
Число без знака с запятой, фиксированной перед старшим разрядом:

| 
| 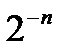
|
Число со знаком с запятой, фиксированной перед старшим разрядом:
| знак | 
| 
| 
|
Число без знака с запятой, фиксированной после младшего разряда:

| 
| . | . | . | . | 
|
Число со знаком с запятой, фиксированной после младшего разряда:
| 1. Знак | 
| 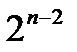
| . | . | . | 
|
В первом варианте могут быть представлены только правильные дроби, во втором – целые числа, смешанное число в такой разрядной сетке не представимо.
Нормальная форма представления чисел позволяет отображать смешанные числа и, кроме того, значительно расширяет диапазон представления чисел. Числа представляются в виде мантиссы и степени (порядка) числа в двоичной системе счисления. Мантисса обычно представляется правильной дробью в нормализованном виде (отсюда и название формы представления). В нормализованном виде первая цифра мантиссы (справа от запятой) должна быть отличной от нуля. Это позволяет избежать множественных форм представления чисел с плавающей точкой. Разрядная сетка ЭВМ для такого представления может быть следующей:
| знак числа | 
| 
| . | . | . | 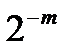
| Знак поряд- ка | 
| 
| . | . |  
|
При m=22 и p=10 диапазон чисел составляет от  до
до  . Для сравнения: количество секунд, которые прошли с момента образования планеты Земля составляет всего
. Для сравнения: количество секунд, которые прошли с момента образования планеты Земля составляет всего  .
.
Следует отметить, что все числа с плавающей запятой хранятся в машине в нормализованном виде. Нормализованными называются такие числа, в старший разряд мантиссы которого не равен 0. У нормализованных двоичных чисел, следовательно, 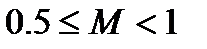 .
.
|
|
|


