 |
Краткие сведения из теории
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №5
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СТАЦИОНАРНЫХ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ, ЗАДАННЫХ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ ИЛИ ПЕРЕДАТОЧНЫМИ ФУНКЦИЯМИ
Цель работы
Приобретение практических навыков исследования устойчивости непрерывных стационарных линейных динамических систем (ЛДС) различными методами и установление факта, что устойчивая стационарная ЛДС является асимптотически устойчивой.
Краткие сведения из теории
Исследование устойчивости является одной из важнейших задач анализа ЛДС.
Устойчивость – это свойство динамической системы возвращаться в исходное равновесное состояние покоя после кратковременного воздействия на нее возмущения или после выведения ее из исходного состояния ненулевыми начальными условиями.
Динамическая система называется устойчивой, если при ненулевых ограниченных начальных условиях ее свободное движение ограничено. При этом, если это собственное движение с ростом времени стремится к нулю, то такая система называется асимптотически устойчивой. Следует отметить, что устойчивость непрерывных стационарных ЛДС всегда является асимптотической. Другими словами свободное движение устойчивых систем указанного класса всегда затухает до нуля. Проверку этого свойства устойчивой ЛДС можно выполнить путем построения ее переходной характеристики.
Исследование устойчивости ЛДС проводится при помощи их математических моделей, которые устанавливают связь вход-выход и могут быть представлены в виде линейных дифференциальных уравнений с постоянными коэффициентами, в виде передаточных функций или структурных схем. Например, в уравнении (1) искомая функция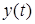 
играет роль выхода, а функция 
– входа. В теории автоматического управления, как правило, устойчивость исследуется для замкнутых систем, то есть систем автоматического управления с отрицательной обратной связью.
|
|
|
Необходимым и достаточным условием устойчивости замкнутой САУ, относящейся к классу ЛДС, является расположение в левой полуплоскости комплексной плоскости характеристических чисел линейного дифференциального уравнения (если модель САУ задана в виде дифференциального уравнения) или полюсов передаточной функции замкнутой САУ.
В случае, если замкнутая САУ задана линейным дифференциальным уравнением с постоянными коэффициентами в виде
(1)
с начальными условиями
(2)
то характеристическое уравнение для (1) записывается следующим образом:
. (3)
Корни характеристического уравнения (3), которое является алгебраическим, называются характеристическими числами.
Если к левой и правой части дифференциальному уравнению (1) применить преобразование Лапласа при нулевых начальных условиях (начальные условия (2) соответствуют нулевым), то можно получить передаточную функцию как отношение изображения по Лапласу выхода 
к изображению входа 
. Имеем
. (4)
Знаменатель передаточной функции (4) называется характеристическим полиномом, а уравнение
(5)
называется характеристическим уравнением передаточной функции (4).
Корни характеристического уравнения (5) называются полюсами передаточной функции (4).
Таким образом, характеристические числа дифференциального уравнения (1) и полюсы, соответствующей ему передаточной функции (4), совпадают. Это означает, что анализ устойчивости замкнутой САУ можно проводить при помощи различных моделей, относящихся к одной и той же динамической системе.
Следует отметить, что с помощью полинома числителя передаточной функции (4) можно построить алгебраическое уравнение
|
|
|
,
корни которого (в рассматриваемом примере только один корень 
) называют нулями, так как при подстановке их в передаточную функцию (4) последняя обращается в ноль. Подстановка полюсов в передаточную функцию (4) обращает ее в бесконечность.
Из анализа алгебраического уравнения (5) следует, что число полюсов передаточной функции (4) равно 3, а их расположение на комплексной плоскости зависит от значений коэффициентов 
, где 
. Принимая во внимание, что полюсы могут быть как вещественными, так и комплексными, а также тот факт, что комплексные полюсы существуют всегда парами, принимающими комплексно-сопряженные значения, можно проиллюстрировать на рис.1 возможные варианты взаимного их размещения на комплексной плоскости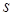 
для устойчивой замкнутой САУ.
Рис.1. Варианты расположения полюсов передаточной функции (4) устойчивой замкнутой САУ
На рис.1а) расположены 3 вещественных полюса. На рис.1б) показано расположение одного вещественного и пары комплексно-сопряженных полюсов. На рис.1в) так же изображены один вещественный полюс и пара комплексно-сопряженных, но модуль вещественного полюса меньше, чем у вещественного полюса, изображенного на рис. 1б).
Таким образом, анализ устойчивости непрерывной стационарной линейной САУ можно свести к решению задачи вычисления характеристических чисел или полюсов при помощи дифференциального уравнения или передаточной функции соответственно, описывающих ее поведение (динамику). Если исследуемая САУ задана передаточной функцией, то эффективным средством решения этой задачи являются следующие функции системы MATLAB:
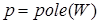или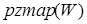 
,
где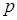 
– вектор столбец, элементы которого искомые полюсы;
– переменная MATLAB, определяющая исследуемую передаточную функцию, например, при помощи следующей командной строки:
,
где 
– коэффициенты полинома числителя исследуемой передаточной функции(записываются через пробел);
– коэффициенты полинома знаменателя исследуемой передаточной функции (записываются через пробел).
Функция 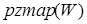выводит на экран компьютера карту взаимного расположения нулей и полюсов исследуемой передаточной функции .
В случае, когда вычисление полюсов затруднено, применяются критерии устойчивости, которые без прямого вычисления характеристических чисел или полюсов позволяют судить об их расположении на комплексной плоскости. Такие критерии разделяются на алгебраические и частотные.
|
|
|
Первый алгебраический критерий устойчивости в 1876 году был предложен русским ученым и государственным деятелем Иваном Алексеевичем Вышнеградским (1831 – 1895), который считается основоположником теории автоматического регулирования.
Исследование расположения корней характеристического уравнения (3) системы третьего порядка на комплексной плоскости положено в основу метода Вышнеградского. Поделив уравнение (3) на 
и вводя новую переменную
его можно преобразовать к нормализованной форме
или
, где 
, 
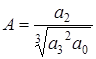. (6)
Исследуя нормализованное характеристическое уравнение И. А. Вышнеградский определил условия устойчивости для систем, описываемых линейными дифференциальными уравнениями третьего порядка с постоянными коэффициентами в виде неравенств.
1. Линейная стационарная система будет устойчивой, если 
.
2. Линейная стационарная система будет неустойчивой, если 
.
3. Линейная стационарная система будет находиться на границе устойчивости, если 
.
И. А. Вышнеградскому принадлежит диаграмма, определяющая области устойчивости стационарной линейной динамической системы третьего порядка. Анализируя решение кубического уравнения (6) он доказал, что область устойчивости разделяется на зоны с различным характером протекания переходных процессов в зависимости от расположения корней характеристического уравнения (характеристических чисел).
На диаграмме, изображенной на рис.2, граница устойчивости в плоскости двух параметров 
и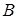 
представляется равнобокой гиперболой, разделяющей площадь диаграммы на две области: область устойчивости, лежащую выше гиперболы, и область неустойчивости, лежащую ниже гиперболы.
Выпуклость этой гиперболы обращена к области неустойчивости.
На диаграмме также выделена область III монотонного процесса, протекающего при отсутствии колебаний. Эта область начинается в точке (3,3),
|
|
|
где все три корня характеристического уравнения вещественны, отрицательны и кратны.
Область II характерна тем, что имеется один отрицательный корень вещественный и пара комплексно-сопряженных с отрицательными вещественными частями, причем модуль вещественного корня больше модулей комплексных корней (вещественный корень дальше от мнимой оси).
Выделенная область диаграммы I так же, как и II область содержит один вещественный отрицательный корень и пару комплексно-сопряженных корней с отрицательными вещественными частями, модули которых больше модуля вещественного корня (вещественный корень ближе к мнимой оси комплексной плоскости s).
Графики переходных процессов, характеризующих собственное движение исследуемой ЛДС при различном расположении корней характеристического уравнения на комплексной плоскости s, приведены на рис. 3.
Таким образом, диаграмма И. А. Вышнеградского позволяет установить связь между параметрами ЛДС и качеством соответствующих переходных процессов.
Рис.2. Диаграмма Вышнеградского
Рис. 3. Вид переходных процессов, характеризующих собственное движение ЛДС в зависимости от зоны расположения ее характеристических чисел на диаграмме Вышнеградского.
На основе подобия уравнений (3) и (6), а также необходимого и достаточного условия устойчивости, формулировку условий устойчивости Вышнеградского можно привести в форме критерия.
Критерий Вышнеградского для системы 3 порядка. Для устойчивости ЛДС с характеристическим уравнением (3) необходимо и достаточно, чтобы выполнялось следующее неравенство:
.
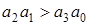Немецкий математик Адольф Гурвиц (1859 – 1919) предложил в 1895 году алгебраическую форму критерия устойчивости для ЛДС, который основан на вычислении определителей, составленных из коэффициентов характеристического уравнения произвольного порядка. При этом для характеристического уравнения 
порядка составляется квадратная матрица коэффициентов, содержащая строк и столбцов в виде
.
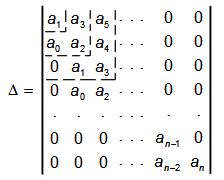Эта матрица составляется следующим образом. По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты по порядку от 
до 
. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также если индекс его меньше нуля или больше , на месте его пишется нуль.
Определители Гурвица составляются по следующему правилу:
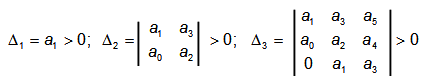
Последний определитель включает в себя всю матрицу.
Критерий Гурвица для системы порядка.
|
|
|
1. ЛДС будет устойчивой, если диагональные определители Гурвица больше нуля.
2. ЛДС будет неустойчивой, если хотя бы один из диагональных определителей Гурвица меньше нуля.
3. ЛДС находится на границе устойчивости, если хотя бы один из диагональных определителей равна нулю.
Условия устойчивости, сформулированные в критерии Гурвица, являются необходимыми и достаточными.
Можно показать, что положительность всех без исключения коэффициентов характеристического уравнения ЛДС является необходимым условием ее устойчивости, но не достаточным. При этом положительность коэффициентов характеристического уравнения ЛДС первого и второго порядков является не только необходимым условием устойчивости, но и достаточным.
Исследование устойчивости ЛДС с характеристическим уравнением третьего порядка удобно проводить при помощи критерия Вышнеградского, а критерий Гурвица целесообразно применять для ЛДС с характеристическим уравнением четвертого порядка.
|
|
|
12 |
