 |
Задание на выполнение лабораторной работы
|
|
|
|
1. Используя коэффициенты характеристического уравнения заданной передаточной функции (см. вариант задания), вычислить при помощи программы, помещенной в 
- файл, параметры Вышнеградского 
и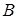 
.
2. Исследовать устойчивость ЛДС при помощи проверки выполнения условий Вышнеградского, а также критериев Вышнеградского и Гурвица. Рекомендуется это выполнить средствами MATLAB(см. методический пример).
3. При помощи найденных параметров и 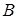определить вид и расположение корней характеристического уравнения на диаграмме Вышнеградского (рис. 2), а также предполагаемый характер переходного процесса (собственного движения) в исследуемой ЛДС (рис. 3).
4. По заданному аналитическому выражению передаточной функции исследуемой ЛДС определить ее модель 
в среде MATLAB при помощи функции 
, помещенной в m – файл.
5. Рассматривая корни характеристического уравнения как полюсы передаточной функции исследуемой ЛДС, при помощи функции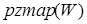 
построить карту расположения этих корней (полюсов) на комплексной плоскости и сравнить с результатами применения диаграммы Вышнеградского.
6. Исследовать характер переходного процесса (собственного движения) исследуемой ЛДС при помощи функции 
и сравнить с результатом применения диаграммы Вышнеградского.
7. Оформить отчет и сделать выводы.
Контрольные вопросы
1. Что понимается под устойчивостью?
2. Какая динамическая система называется устойчивой?
3. Что такое характеристическое уравнение?
4. Какой вид имеют корни характеристического уравнения?
5. Чем отличаются правые и левые корни характеристического уравнения?
6. Сформулируйте условие устойчивости систем по Ляпунову.
7. Что такое граница устойчивости?
|
|
|
8. Что такое критерии устойчивости?
9. Сформулируйте необходимое и достаточное условие устойчивости ЛДС.
10. Сформулируйте критерий Вышнеградского.
11. Что такое диаграмма Вышнеградского и чем она полезна?
12. Сформулируйте критерий Гурвица.
13. В чем достоинства и недостатки алгебраических критериев устойчивости?
14. Какие функции системы MATLAB можно использовать для анализа устойчивости стационарной ЛДС?
15. Как по заданному линейному дифференциальному уравнению с постоянными коэффициентами определить устойчивость его решения?
16. Как определить устойчивость ЛДС, если ее математическая модель задана в виде передаточной функции?
17. Как определить устойчивость ЛДС, если ее математическая модель задана в виде дифференциального уравнения?
18. Как по линейному дифференциальному уравнению с постоянными коэффициентами построить передаточную функцию?
19. Как по заданной передаточной функции построить соответствующее дифференциальное уравнение?
Приложение А
Методический пример
Листинг программы
Editor
%Лабораторная работа №5
%Параметры передаточной функции
a0=2; a1=3; a2=3; a3=1; b0=1; b1=0;
%Коэффициенты Вышнеградского
A1=(a3^2*a0)^(1/3); B1=(a0^2*a3)^(1/3);
A=a2/A1
B=a1/B1
AB=A*B
%Проверка выполнения условий
%Вышнеградского
if A*B>1
disp('Stabil')
else
disp('No Stabil')
end
%Критерий Вышнеградского
G1=a1*a2; G2=a0*a3;
if G1>G2
disp('Stabil')
else
disp('No Stabil')
end
%Критерий Гурвица
D1=a1
D2=a1*a2-a3*a0
D3=a3*D2
if D1>0 & D2>0 & D3>0
disp('Stabil')
else
disp('No Stabil')
end
%Модель ЛДС в виде ПФ
W=tf([0 1],[a3 a2 a1 a0])
%Карта расположения полюсов
p=pole(W)
figure (1) % Карта расположения корней
% х-кого уравнения
pzmap(W)
%Переходный процесс - импульсная х-ка)
figure (2)
impulse(W)
Результат работы программы, показанный в командном окне
Command window
>> LR_5_Stability
A =
2.3811
B =
1.8899
AB =
4.5000
Stabil
Stabil
|
|
|
D1 =
D2 =
D3 =
Stabil
W =
---------------------
s^3 + 3 s^2 + 3 s + 2
Continuous-time transfer function.
p =
-2.0000
-0.5000 + 0.8660i
-0.5000 - 0.8660i
>>
>>
Приложение Б
Варианты задания
Передаточная функция исследуемой ЛДС 
Таблица Б1
| № варианта | Параметры передаточной функции | |||||
| 
| 
| 
| 
| 
| |
|
|
|
12 |
