 |
Приведение задачи ЛП к каноническому виду. Метод дополнительных и искусственных переменных
|
|
|
|
Постановка задачи ЛП; идея симплекс-метода; алгоритм симплекс-метода
Задачей ЛП наз-ся задача c1x1+ c2x2+… +cnxn – min при ограниченияех
| a11x1+ a12x2+…+ a1nxn £ b1 a21x1+ a22x2+…+ a2nxn £ b2 … am1x1+ am2x2+…+ amnxn £ bm |
и x1,…, xn³0, где ci, aij, bi – вещественные числа
Будем рассм задачу минимизации, т.к. задачу максимизации можно свести к ней путем домножения на -1.
Задачу можно представить в матричной форме: обозн. x=(x1, …, xn), c=(c1,…,cn), b=(b1,…,bm), A={aij}. Тогда задача будет: <c,x> - min, Ax£b, x³0
От задачи с нер-ми можно перейти к задаче с рав-ми путем введения доп. переменных xn+1, xn+2, …, xn+m >0. Тогда получим задачу:
c1x1+ c2x2+… cnxn+0*xn+1+…+xn+m – min
|
| a11x1+ a12x2+…+ a1nxn+xn+1 = b1 a21x1+ a22x2+…+ a2nxn +xn+2 = b1 … am1x1+ am2x2+…+ amnxn +xn+m= bm |
x1,…, xn+m³0
Можно доказать, что решив эту задачу, будет решена и исходная.
Обозн 
| тогда задачу можно представить в виде: c1x1+ c2x2+… cnxn – min P1x1 + P2x2+…+Pnxn = P0 x1…xn ³0 |
Вектор x, удовл-ий ограничениям задачи наз‑ся допустимым решением, или планом. Мн-во всех планов – мн-во допустимых решений (мн-во планов). План, который доставляет минимум целевой ф-ии – решение. План наз‑ся опорным, если векторы Pj, соотв-ие ненулевым компонентам плана, линейно независимы. Пусть ранг матр. A = m. Опорный план наз‑ся невырожденным, если число ненулевых компонент k в этом плане совпадает с m; и называется вырожденным, если k > m.
Симплекс-метод:
предположим, что среди векторов столбцов ограничений есть векторы P1, …, Pm, которые образуют единичный базис и коэфф. разложения вектора P0 по этому базису не отрицательны.
| Если оказалось, что все оценки в строке критериев не положительны, то по теореме об оптимальности, опорный план, соответствующий исх‑му базису, оптимален. В противном случае, в строке критериев нужно выбрать любую положительную оценку. |
|
Пусть эта оценка Dj. Это озн‑ет, что DPj следует вводить в базис на следующем шаге. Выбранный столбец Pj принято называть ведущим на этом шаге. Для ведущего столбца вычисляется значение qj=min(xi0/xij) по i: xij > 0. Пусть минимум достигается при i=s. Число xsj в ведущем столбце принято называть ведущим элементом таблицы на данном шаге.
После того, как найден ведущий элемент, найден и вектор Ps, выводящийся из базиса. В следующей симплекс-таблице в первом столбце будет стоять новый базис P1, …, Ps-1, Pj, Ps+1, …,Pm.
Для нового базиса при заполнении новой таблицы придется отыскивать коэффициенты разложения.
Для получения новых коэфф-ов разложения нужно сделать следующее:
Вся строчка с номером s делится на ведущий элемент xsj, затем с пом. полученной на месте sj единички элементарными преобразованиями строк добиваемся чтобы во всех остальных строчках ведущий столбец получились нули. Новая матрица будет состоять из искомых коэф‑оф разложения.
Пр. min(2x1 - 3x2 + x3 + 5x4 - 2x5)
x1…x5 ³ 0
|
На втором шаге найден оптимальный опорный план.
|
Приведение задачи ЛП к каноническому виду. Метод дополнительных и искусственных переменных
|
|
|
Задачей ЛП наз-ся задача c1x1+ c2x2+… +cnxn – min при ограниченияех
|
| a11x1+ a12x2+…+ a1nxn £ b1 a21x1+ a22x2+…+ a2nxn £ b2 … am1x1+ am2x2+…+ amnxn £ bm |
и x1,…, xn³0, где ci, aij, bi – вещественные числа
Задача ЛП имеет канонический вид, если: 1) ограничения, задающиеся матрицей A имеют форму равенств. 2)столбец P0=(b1,…,bm) ³ 0 и 3) xi ³0
Любую задачу ЛП можно привести к каноническому виду:
1. пусть среди основных ограничений есть ограничения вида ³ или £. Тогда в соответствующие строчки нужно либо добавить, либо вычесть доп. новые переменные, потребовать их неотрицательность. В целевую ф‑ию эти новые переменные войдут с коэфф‑ми ноль.
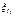2. избавиться от отрицательных чисел в столбце P0 можно домножением соответствующих строк на -1.
3. Пусть, например, на переменную не накладывается условие неотрицательности. Тогда делается замена этой переменной вида
, где
Пр.
| min(x1 - 2x2) | min(x1 - 2x2 + 0*x3) | min(x¢1 - x²1 – 2x2 + 0*x3) | ||||||||
| ® |
| ® |
| ||||||
| x1 ³ 0 | x2, x3 ³ 0 | x¢1, x²1, x2, x3 ³ 0 |
Метод искусственного базиса: этот метод применяется в тех случаях, когда среди векторов столбцов ограничений исходной задачи нет единичного базиса. Согласно этому методу с пом. введения так называемых искусственных переменных на основе исходной задачи строится новая, обладающая таким базисом. Затем решается новая задача и при ее решении получается автоматически и решение исходной задачи.
c1x1+ c2x2+… +cnxn – min
|
| a11x1+ a12x2+…+ a1nxn = b1 a21x1+ a22x2+…+ a2nxn = b1 … am1x1+ am2x2+…+ amnxn = bm |
x1,…, xn³0
Введем m искусственных переменных xn+1,…, xn+m ³ 0 и перейдем к новой задаче:
c1x1+ c2x2+… + cnxn + wxn+1 + … + wxn+m – min
|
| a11x1+ a12x2+…+ a1nxn + xn+1 = b1 a21x1+ a22x2+…+ a2nxn + xn+1 = b2 … am1x1+ am2x2+…+ amnxn + xn+m = bm |
x1,…,xn,xn+1,…,xn+m ³0, где w - сколь угодно большое положительное число.
Можно доказать, что если (x*1,…, x*n, x*n+1,…, x*n+m) – решение полученной задачи, то (x*1,…, x*n) – решение исходной.
Постановка задачи выпуклого программирования. Определение и примеры выпуклых множеств и выпуклых функций. Выпуклость и замкнутость лебегова множества выпуклой функции. Градиентное неравенство для выпуклых функций. Экстремальные свойства выпуклых функций (теорема о глобальном и локальном минимуме)
|
|
|
Мн‑во GÌRn наз‑ся выпуклым, если " x 1, x 2 ÎG и "lÎ(0,1) выполняется l x 1+(1‑l) x 2ÎG. Пустое мн-во и мн-во, состоящее из одной точки считаются выпуклыми.
выпуклое не выпуклое
Ф-ия f(x) наз‑ся выпуклой на выпуклом мн-ве GÌRn, если " x 1, x 2 ÎG, "lÎ(0,1) выполняется: f(l x 1 + (1-l) x 2) £ lf(x 1) + (1-l)f(x 2). Ф‑ия наз‑ся строго выпуклой, если неравенство – строгое.
Пр. f(x) = ác, x ñ = c1x1 + … + cnxn. покажем выпуклость этой ф-ии. Выберем произв. x 1, x 2ÎRn и lÎ(0,1)
f(l x 1 + (1-l) x 2) = ác, l x 1 + (1-l) x 2ñ = lác, x 1ñ + (1-l) ác, x 2ñ = lf(x 1) + (1-l) f(x 2)
Т.е. неравенство, необходимое для выпуклости ф‑ии выполняется как равенство, следовательно функция выпукла.
Теорема: ф-ия f(x) явл-ся выпуклой в Rn т.тогда, когда " x,SÎRn, ф‑ия Y(m) = f(x + mS), где mÎR1, является выпуклой в R1
Теорема: (о выпуклости и замкнутости Лебегова мн‑ва выпуклой ф‑ии)
Пусть GÌRn – выпуклое и замкнутое мн‑во, а f(x) – выпуклая на G непрерывная ф‑ия. Тогда мн-во L º { x ÎG: f(x) £ b = const} является выпуклым и замкнутым множеством.
|
|
|
