 |
Метод решения задач выпуклого программирования (условная минимизация) на выбор: метод условного градиента, метод проекции градиента, метод штрафных функций
|
|
|
|
Мн‑во GÌRn наз‑ся выпуклым, если "x1,x2 ÎG и "lÎ(0,1) выполняется lx1+(1‑l)x2ÎG. Пустое мн-во и мн-во, состоящее из одной точки считаются выпуклыми.
выпуклое не выпуклое
Ф-ия f(x) наз‑ся выпуклой на выпуклом мн-ве GÌRn, если "x1,x2 ÎG, "lÎ(0,1) выполняется: f(lx1 + (1-l)x2) £ lf(x1) + (1-l)f(x2). Ф‑ия наз‑ся строго выпуклой, если неравенство – строгое.
Постановка задачи выпуклого программирования: задача мат. программирования вида наз‑ся задачей выпуклого программирования, если f(x) – выпуклая ф‑ия и DÌRn – выпуклое мн‑во.
Метод штрафных функций решает задачу условной минимизации
D = {xÎRn: fi(x)£bi, i=1,…,m}
Метод сводит решение исходной задачи к последовательному решению задач безусловной минимизации.
Положим
Методы заключаются в следующем:
выбирается числовая последовательность {mk}, k=0,1,… такая, что mk > 0 "k,
.
На k-ом шаге метода строится вспомогательная функция
и в качестве точки xk выбирается точка минимума ф‑ии на всем пр‑ве Rn.
Все методы этого класса отл‑ся дгур от друга способом задания штрафных ф‑ий. Эти методы сходящиеся.
доминирующих над др. дележами (с-ядро) или множеству не доминирующих друг над другом дележей, которые в совокупности
доминируют над всеми остальными дележами (решения по Нейману - Моргенштерну) или к множеству дележей, в которых в некотором смысле минимизируется «недовольство» коалиций (n-ядро) и т. д. Некоторые из принципов оптимальности не всегда реализуются; другие реализуются иногда неоднозначно. Нахождение реализаций часто затруднительно. Т. о., математическая проблема установления оптимального поведения в кооперативных играх является весьма сложной как принципиально, так и технически.
|
|
|
Многокритериальная оптимизация. Матричные игры. Кооперативные игры.
Многокритериальная оптимизация.
Часто возникает задача обеспечить оптимальность объекта проектирования одновременно по нескольким критериям оптимальности 
. Обычно эти критерии противоречивы и оптимизация по каждому из них приводит к различным значениям вектора варьируемых параметров 
. Поэтому выделяется отдельный класс задач многокритериальной оптимизации.
Постановка задачи многокритериальной оптимизации.
Будем называть каждый из скалярных критериев оптимальности 
частным критерием оптимальности. Совокупность частных критериев оптимальности 
будем называть векторным критерием оптимальности. Положим, что ставится задача минимизации каждого из частных критериев оптимальности ф1(X), ф2(X),..., фs(X) в одной и той же области допустимых значений 
. Решение задачи многокритериальной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, а оказывается некоторым компромиссом для вектора 
в целом. Задачу многокритериальной оптимизации будем записывать в виде 
Где 
— множество допустимых значений вектора варьируемых параметров Х. Прежде, чем применить тот или иной метод решения задачи (1), обычно производят нормализацию частных критериев, приводя все частные критерии оптимальности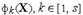 
к одному масштабу. Чаще всего при этом используют относительные отклонения частных критериев от их минимальных значений:
Где 
Метод относится к классу стохастических методов оптимизации
Сохраним за нормализованными частными критериями оптимальности обозначения 
.
Матричные Игры
Матричные игры, понятие игр теории. Матричные игры — игры, в которых участвуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное число чистых стратегий. Если игрок I имеет m стратегий, а игрок II — n стратегий, то игра может быть задана (m ´ n)-мaтрицей А = ||aij||, где aij есть выигрыш игрока I, если он выберет стратегию i (i = -1,..., m), а игрок II — стратегию j (j = 1,..., n). Следуя общим принципам поведения в антагонистических играх (частным случаем которых являются Матричные игры), игрок I стремится выбрать такую стратегию i0, на которой достигается
|
|
|
игрок II стремится выбрать стратегию jo, на которой достигается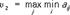 
Если u1 = u2, то пара (i0, j0) составляет седловую точку игры, то есть выполняется двойное неравенство
; i = 1, …, m; j = 1, …, n.
Число 
называется значением игры; стратегии i0, j0 называются оптимальным и чистыми стратегиями игроков I и II соответственно. Если u1 ¹ u2, то всегда u1 < u2; в этом случае в игре седловой точки нет, а оптимальные стратегии игроков следует искать среди их смешанных стратегий (то есть вероятностных распределений на множестве чистых стратегий). В этом случае игроки оперируют уже с математическими ожиданиями выигрышей.
Основная теорема теории Матричные игры (теорема Неймана о минимаксе) утверждает, что в любой Матричные игры существуют оптимальные смешанные стратегии х*, у*, на которых достигаемые «минимаксы» равны (общее их значение есть значение игры). Например, игра с матрицей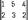 
имеет седловую точку при i0 = 2, j0 = 1, а значение игры равно 2; игра с матрицей 
не имеет седловой точки. Для неё оптимальные смешанные стратегии суть х* = (3/4, 1/4), y* = (1/2, 1/2); значение игры равно 1/2.
Для фактического нахождения оптимальных смешанных стратегий чаще всего используют возможность сведения Матричные игры к задачам линейного программирования. Можно использовать так называемый итеративный метод Брауна — Робинсон, состоящий в последовательном фиктивном «разыгрывании» данной игры с выбором игроками в каждой данной партии своих чистых стратегий, наилучших против накопленных к этому моменту стратегий оппонента. Игры, в которых один из игроков имеет только две стратегии, просто решить графически.
Кооперативные игры
Кооперативная теория игр, раздел игр теории, в котором игры рассматриваются без учёта стратегических возможностей игроков (тем самым Кооперативная теория игр изучает некоторый класс моделей общих игр). В частности, в Кооперативную теорию игр входит исследование нестратегических (кооперативных) игр, лишённых с самого начала стратегического аспекта. В кооперативной игре задаются возможности и предпочтения различных групп игроков (коалиций) и из них выводятся оптимальные (устойчивые, справедливые) для игроков ситуации, в том числе распределения между ними суммарных выигрышей: устанавливаются сами принципы оптимальности, доказывается их реализуемость в различных классах игр и находятся конкретные реализации. В терминах кооперативных игр поддаются описанию многие экономические и социологические явления.
|
|
|
Наиболее просто описание т. н. классических кооперативных игр, состоящее в указании: 1) множества игроков J; 2) семейства Rn подмножеств J (коалиций интересов) и 3) функции u, заданной на Rn и принимающей вещественные значения. [u(K) можно понимать (иногда - с некоторыми оговорками) как сумму, которую коалиция К может распределить между своими членами.] Обычно (не всегда) функцию u считают супераддитивной: u(K 
L) ³ u(K) + u(L) при К 
L = Æ. Это отражает дополнительные возможности, возникающие у коллективов при их объединении. Для классических кооперативных игр характерна возможность неограниченных передач выигрышей одними игроками другим и притом без изменения их полезности (ценности). Более общим типом игр являются игры без побочных платежей, где на такие передачи накладываются некоторые ограничения.
Пусть J = {1,..., n}; вектор х= (х1,..., xn), для которого
Siezxit = u(J)
и xi ³ u({i}) при всех i 
J, называется дележом. Говорят, что делёж х доминирует над дележом у = (y1,..., yn), если найдётся такая (предпочитающая его) коалиция К, что
Siekxi £ u(K)
и x i>yi для i K. Оптимальное поведение участников кооперативной игры может состоять в стремлении к множеству дележей, не
|
|
|
