 |
Оценка погрешности при решении системы линейных уравнений
|
|
|
|
Для того, чтобы оценить погрешности вычислений решения системы линейных уравнений, нам нужно ввести понятия соответствующих норм матриц.
Прежде всего, вспомним три наиболее часто употребляемые нормы для вектора  :
:
 (11)
(11)
 (Евклидова норма) (12)
(Евклидова норма) (12)
 (Чебышевская норма) (13)
(Чебышевская норма) (13)
Для всякой нормы векторов можно ввести соответствующую норму матриц:
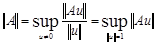 (14)
(14)
которая согласована с нормой векторов в том смысле, что
 (15)
(15)
Можно показать, что для трёх приведённых выше случаев нормы матрицы  задаются формулами:
задаются формулами:
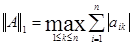 (16)
(16)
 (17)
(17)
 (18)
(18)
Здесь  - являются сингулярными числами матрицы
- являются сингулярными числами матрицы  , т.е. это положительные значения квадратных корней
, т.е. это положительные значения квадратных корней  - матрицы
- матрицы  (которая является положительно-определённой матрицей, при
(которая является положительно-определённой матрицей, при  ).
).
Для вещественных симметричных матриц  - где
- где 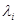 - собственные числа матрицы
- собственные числа матрицы  .
.
Абсолютная погрешность решения системы:
 (19)
(19)
где  - матрица системы,
- матрица системы,  - матрица правых частей, оценивается нормой:
- матрица правых частей, оценивается нормой:
 (20)
(20)
Относительная погрешность оценивается по формуле:
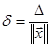 (21)
(21)
где  .
.
Итерационные методы решения систем линейных уравнений
Рассмотрим систему линейных уравнений, которая плохо решается методами Гаусса. Перепишем систему уравнений в виде:
 (22)
(22)
|
|
|
где  - заданная числовая матрица
- заданная числовая матрица  -го порядка,
-го порядка,  - заданный постоянный вектор.
- заданный постоянный вектор.
Метод простой итерации Якоби
Этот метод состоит в следующем: выбирается произвольный вектор  (начальное приближение) и строится итерационная последовательность векторов по формуле:
(начальное приближение) и строится итерационная последовательность векторов по формуле:
 ,
,  (23)
(23)
Приведём теорему, дающую достаточное условие сходимости метода Якоби.
Теорема. Если  , то система уравнений (22) имеет единственное решение
, то система уравнений (22) имеет единственное решение  и итерации (23) сходятся к решению.
и итерации (23) сходятся к решению.
Легко заметить, что эта теорема является простым обобщением теоремы о сжатых отображениях изученных нами раньше для одношагового итерационного процесса в общем виде. Все оценки, полученные ранее, переносятся и для системы уравнений, разница лишь в понятиях соответствующих норм. Обобщая метод простой итерации Якоби для случая системы уравнений:
 (24)
(24)
Строим алгоритм решения:
а) переписываем уравнение (24) в однородном виде и умножаем на постоянную  - которую далее найдём из условий сходимости итерационного процесса:
- которую далее найдём из условий сходимости итерационного процесса:
 (25)
(25)
б) добавляем 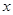 к обеим частям (25) и получаем:
к обеим частям (25) и получаем:
 (26)
(26)
в) строим итерационную формулу Якоби:
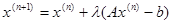 (27)
(27)
где постоянную  находим из условий сходимости итерационного процесса (27), который в данном случае имеет вид:
находим из условий сходимости итерационного процесса (27), который в данном случае имеет вид:
 (28)
(28)
где 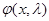 - вектор-функция из (26) или исходя из теоремы о сжатых отображениях
- вектор-функция из (26) или исходя из теоремы о сжатых отображениях  , где
, где  - единичная матрица.
- единичная матрица.
Рассмотрим числовой пример:
Пусть имеем систему уравнений:

Переписываем систему в виде:

Составляем итерационную формулу:

Коэффициент  выбираем из условий:
выбираем из условий:  , т.е.
, т.е.

 .
.
Метод Гаусса-Зейделя
Для решения линейной системы уравнений разработано множество итерационных методов. Тем более, что метод простой итерации Якоби сходится медленно. Одним из таких методов является метод Гаусса-Зейделя.
|
|
|
Для иллюстрации метода рассмотрим числовой пример:
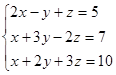 (29)
(29)
Уравнения переписаны таким образом, что на главной диагонали стоят максимальные для каждого уравнения коэффициенты.
Начинаем с приближения 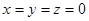 . Используя первое уравнение, находим для
. Используя первое уравнение, находим для 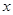 новое значение
новое значение  при условии
при условии  .
.
 (30)
(30)
Беря это значение  и
и  из второго уравнения, находим
из второго уравнения, находим  , далее из третьего уравнения находим
, далее из третьего уравнения находим  ,
,  . Эти три величины дают новое приближение и можно повторить цикл с начала, получаем:
. Эти три величины дают новое приближение и можно повторить цикл с начала, получаем:  ,
,  ,
,  и т.д. Итерации продолжаются до выполнения неравенства
и т.д. Итерации продолжаются до выполнения неравенства  .
.
Общий алгоритм метода Гаусса-Зейделя имеет вид:
Пусть
 (31)
(31)
где у матрицы 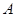 - все диагональные элементы отличны от нуля, т.е.
- все диагональные элементы отличны от нуля, т.е.  (если
(если  , тогда переставляем строки так, чтобы добиться условия
, тогда переставляем строки так, чтобы добиться условия  ). Если
). Если  -ое уравнение системы (31) разделить на
-ое уравнение системы (31) разделить на  , а затем все неизвестные кроме
, а затем все неизвестные кроме  - перенести в правую часть, то мы придём к эквивалентной системе вида:
- перенести в правую часть, то мы придём к эквивалентной системе вида:
 (32)
(32)
где  ,
,  ,
, 
 (33)
(33)
Метод Гаусса-Зейделя состоит в том, что итерации производятся по формуле:
 (34)
(34)
где  - номер итерации, а
- номер итерации, а  .
.
Замечание: для сходимости метода (34) достаточно выполнения хотя бы одного из условий:
а)
 ,
,  (35)
(35)
б) 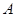 - симметричная и положительно-определённая матрица.
- симметричная и положительно-определённая матрица.
|
|
|


