 |
Деление отрезка в заданном отношении.
|
|
|
|
Раздел 1. Метод координат на плоскости и в пространстве
Понятие об аналитической геометрии
В элементарной (школьной) геометрии изучаются свойства прямолинейных фигур и окружности. Основную роль играют построения, вычисления же, хотя практическое значение их и велико, в теории играют подчиненную, вспомогательную роль. Выбор того или иного построения обычно требует изобретательности. Это и составляет главную трудность при решении задач методами элементарной геометрии.
Аналитическая геометрия возникла из потребности создать единообразные средства для решения геометрических задач с тем, чтобы применить их изучению важных для практики кривых линий различной формы.
Эта цель была достигнута созданием координатного метода. В нем ведущую роль играют вычисления, построения же имеют вспомогательное значение. Вследствие этого решение задач методами аналитической геометрии требует гораздо меньшей изобретательности.
Создание координатного метода было подготовлено трудами древнегреческих математиков, в особенности Аполлония (2-3 в. до н.э.). Систематическое развитие координатный метод получил в первой половине XVII века в работах П. Ферма и Р. Декарта. Они, однако, рассматривали только плоские линии. К систематическому изучению пространственных линий и поверхностей координатный метод был впервые применен Л. Эйлером (1707-1783).
Прямоугольная система координат на плоскости
Метод координат заключается в установлении соответствия между точками прямой (плоскости, пространства) и их координатами – действительными числами при помощи системы координат.
 Две взаимно-перпендикулярные оси
Две взаимно-перпендикулярные оси 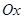 и
и  , имеющие общее начало
, имеющие общее начало  и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
|
|
|
Ось 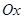 называется осью абсцисс, ось
называется осью абсцисс, ось  называется осью ординат. Обе вместе они называются осями координат.
называется осью ординат. Обе вместе они называются осями координат.
Точка  пересечения осей называется началом координат. Плоскость, в которой расположены оси
пересечения осей называется началом координат. Плоскость, в которой расположены оси 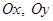 называется координатной плоскостью и обозначается
называется координатной плоскостью и обозначается  .
.
Пусть 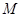 – произвольная точка плоскости. Опустим из нее перпендикуляры
– произвольная точка плоскости. Опустим из нее перпендикуляры 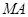 и
и 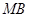 на оси
на оси 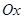 и
и  . Прямоугольными координатами
. Прямоугольными координатами  и
и  точки
точки 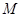 будем называть соответственно величины отрезков
будем называть соответственно величины отрезков  и
и  :
:  Знаки чисел
Знаки чисел  и
и  указывают на какой (положительной или отрицательной) полуоси расположена соответствующая точка.
указывают на какой (положительной или отрицательной) полуоси расположена соответствующая точка.
Координата  точки
точки 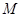 называется ее абсциссой, координата
называется ее абсциссой, координата  точки
точки 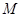 – ординатой.
– ординатой.
Тот факт, что точка 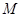 имеет координаты
имеет координаты  и
и  , символически обозначают:
, символически обозначают: 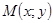 . При этом первой в скобках указывают абсциссу, а второй – ординату. Начало координат имеет координаты
. При этом первой в скобках указывают абсциссу, а второй – ординату. Начало координат имеет координаты  .
.
 Таким образом, при выбранной системе координат каждой точке
Таким образом, при выбранной системе координат каждой точке 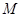 на плоскости соответствует единственная пара чисел
на плоскости соответствует единственная пара чисел 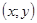 – ее прямоугольные координаты. И, обратно, каждой паре чисел
– ее прямоугольные координаты. И, обратно, каждой паре чисел 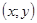 соответствует, и притом одна, точка
соответствует, и притом одна, точка 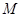 плоскости
плоскости  такая, что ее абсцисса равна
такая, что ее абсцисса равна  , а ордината –
, а ордината –  .
.
Итак, введение прямоугольной системы координат на плоскости позволяет установить однозначное соответствие между множеством всех точек плоскости и множеством пар чисел, что дает возможность при решении геометрических задач применять алгебраические методы.
Оси координат разбивают плоскость на 4 части, их называют четвертями, квадрантами или координатными углами и нумеруют римскими числами I, II, III, IV.
Простейшие задачи аналитической геометрии на плоскости

Расстояние между двумя точками.
Теорема 1. Для любых двух точек  и
и  плоскости расстояние
плоскости расстояние 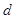 между ними выражается формулой:
между ними выражается формулой:
 . (1.1)
. (1.1)
Например, если даны точки  и
и  , то расстояние между ними:
, то расстояние между ними:
 .
.
Площадь треугольника.
|
|
|
 Теорема 2. Для любых точек
Теорема 2. Для любых точек  , не лежащих на одной прямой, площадь треугольника
, не лежащих на одной прямой, площадь треугольника  выражается формулой:
выражается формулой:
 . (1.2)
. (1.2)
Например, найдем площадь треугольника, образованного точками 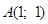 ,
,  и
и  .
.
 .
.
Замечание. Если площадь треугольника равна нулю, это означает, что точки лежат на одной прямой.
Деление отрезка в заданном отношении.
Пусть на плоскости дан произвольный отрезок  и пусть
и пусть 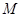 – любая точка этого отрезка, отличная от точек концов. Число
– любая точка этого отрезка, отличная от точек концов. Число  , определенное равенством
, определенное равенством  , называется отношением, в котором точка
, называется отношением, в котором точка 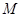 делит отрезок
делит отрезок  .
.
Задача о делении отрезка в данном отношении состоит в том, чтобы по данному отношению  и данным координатам точек
и данным координатам точек 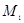 и
и  найти координаты точки
найти координаты точки 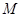 .
.
 Теорема 3. Если точка
Теорема 3. Если точка  делит отрезок
делит отрезок  в отношении
в отношении  , то координаты этой точки определяются формулами:
, то координаты этой точки определяются формулами:  (1.3), где
(1.3), где  – координаты точки
– координаты точки 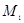 ,
,  – координаты точки
– координаты точки  .
.
Следствие: Если  – середина отрезка
– середина отрезка  , где
, где  и
и  , то
, то  (1.4) (т.к.
(1.4) (т.к.  ).
).
Например. Даны точки  и
и  . Найти координаты точки
. Найти координаты точки 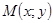 , которая в два раза ближе к
, которая в два раза ближе к  , чем к
, чем к 

Решение: Искомая точка 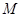 делит отрезок
делит отрезок  в отношении
в отношении  так как
так как 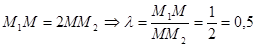 , тогда
, тогда  ,
,  , получили
, получили 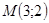 .
.
Полярные координаты
Наиболее важной после прямоугольной системы координат является полярная система координат. Она состоит из некоторой точки  , называемой полюсом, и исходящего из нее луча
, называемой полюсом, и исходящего из нее луча 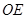 – полярной оси. Кроме того, задается единица масштаба для
– полярной оси. Кроме того, задается единица масштаба для  измерения длин отрезков.
измерения длин отрезков.
Пусть задана полярная система координат и пусть 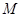 – произвольная точка плоскости. Пусть
– произвольная точка плоскости. Пусть  – расстояние от точки
– расстояние от точки  до точки
до точки 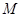 ;
;  – угол, на который нужно повернуть полярную ось для совмещения с лучом
– угол, на который нужно повернуть полярную ось для совмещения с лучом  .
.
Полярными координатами точки 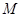 называются числа
называются числа  и
и  . При этом число
. При этом число  считается первой координатой и называется полярным радиусом, число
считается первой координатой и называется полярным радиусом, число  – второй координатой и называется полярным углом.
– второй координатой и называется полярным углом.
Обозначается  . Полярный радиус может иметь любое неотрицательное значение:
. Полярный радиус может иметь любое неотрицательное значение: 
 . Обычно считают, что полярный угол изменяется в следующих пределах:
. Обычно считают, что полярный угол изменяется в следующих пределах:  . Однако в ряде случаев приходится определять углы, отсчитываемые от полярной оси по часовой стрелке.
. Однако в ряде случаев приходится определять углы, отсчитываемые от полярной оси по часовой стрелке.
|
|
|


