 |
Метод координат в пространстве
|
|
|
|
Положение любой точки в пространстве можно однозначно определить с помощью прямоугольной системы координат. Эта система включает три взаимно перпендикулярные оси, пересекающиеся в одной точке О – начале координат. Одну из осей называют осью абсцисс (ось Ох), другую – осью ординат (Оу), третью – осью аппликат (Oz). Плоскости XOY, XOZ и YOZ называются координатными плоскостями. Какой-либо отрезок принимается за единицу масштаба для всех трех осей. Положительные направления на осях выбираются так, чтобы поворот на 900, совмещающий положительный луч OX с положительным лучом OY, казался проходящим против часовой стрелки, если смотреть со стороны луча OZ. Такая система координат называется правой.
Положение любой точки М в пространстве можно определить тремя координатами следующим образом. Через М проводим плоскости, параллельные плоскостям XOY, XOZ и YOZ. В пересечении с осями получаем точки, например, P, Q и R соответственно. Числа х (абсцисса), у (ордината), z (аппликата), измеряющие отрезки OP, OQ и OR в избранном масштабе, называются прямоугольными координатами точки М. Они берутся положительными или отрицательными в зависимости от того, лежат ли соответствующие отрезки на положительной или отрицательной полуоси. Каждой тройке чисел (х; у; z) соответствует одна и только одна точка пространства, и наоборот.
Расстояние между двумя точками 
и 
вычисляется по формуле: 
(1.6)
Координаты (x; y; z) точки М, делящей в заданном отношении 
отрезок АВ, (
, 
) определяются по формулам:
, 
, 
(1.7)
В частности, при 
(точка М делит отрезок АВ пополам), получаются формулы для определения координат середины отрезка:
, 
, 
(1.8)
Пример 4: На оси Оу найти точку, равноудаленную от двух точек 
и 
.
|
|
|
Решение: Точка М, лежащая на оси Оу, имеет координаты 
. По условию задачи |АМ| = |ВМ|. Найдем расстояния |АМ| и |ВМ|, используя формулу (1.6):
Получим уравнение: 
.
Отсюда находим, что 4у = 16, т. е. у = 4. Искомая точка есть М (0; 4; 0).
Пример 5: Отрезок АВ разделен на 3 равные части. Найти координаты точек деления, если известны точки 
и 
.
Решение:
Обозначим точки деления отрезка АВ в следующем порядке: С и D. По условию задачи |АС| = |CD| = |DB|. Поэтому точка С делит отрезок АВ в отношении 
. Пользуясь формулами (1.7), находим координаты точки С:
, 
, 
.
Имеем, 
.
По формулам (1.8) находим координаты точки D – середины отрезка СВ:
, 
, 
.
То есть точка D имеет координаты: 
.
Пример 6: В точках 
, 
, 
, 
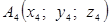сосредоточены соответственно массы m 1, m 2, m 3, m 4. Найти координаты центра тяжести системы этих масс.
Решение:
Как известно из курса физики центр тяжести масс m 1 и m 2, помещенных в точках А и В, делит отрезок АВ на части, обратно пропорциональные массам, сосредоточенным на концах отрезка (
). Исходя из этого, найдем сначала центр тяжести 
системы двух масс m 1 и m 2, помещенных в точках А1и А2:
, 
, 
.
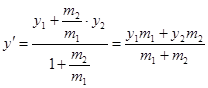Центр тяжести системы трех масс m 1 и m 2 и m 3 (
) находим аналогично:
, 
, 
.
Находим, наконец, центр тяжести системы трёх масс m1, m2, m3 и m4:
, 
, 
.
Вопросы для контроля:
1. Опишите прямоугольную систему координат на плоскости и все ее компоненты.
2. Как определяются координаты произвольной точки плоскости?
3. Напишите формулу для нахождения расстояния между двумя точками наплоскости.
4. Как найти координаты точки, делящей в заданном отношении отрезок?
5. Напишите формулы координат середины отрезка.
6. Напишите формулу, по которой вычисляется площадь треугольника, если известны координаты его вершин.
7. Опишите полярную систему координат.
8. Что называют полярным радиусом? В каких пределах он измеряется?
9. Что называют полярным углом? Пределы его измерения?
10. Как найти прямоугольные координаты точки, для которой известны полярные координаты?
|
|
|
11. Как найти полярные координаты точки, для которой известны прямоугольные координаты?
12. Как найти расстояние между точками в полярной системе координат?
13. Опишите прямоугольную систему координат в пространстве и все ее компоненты.
14. Как определить координаты точки в пространстве?
15. Запишите формулу для нахождения расстояния между двумя точками в пространстве.
16. Запишите формулы для нахождения координат точки, делящей отрезок в данном отношении для трехмерной системы координат.
|
|
|
