 |
Глава 4. Функции, последовательности, пределы
|
|
|
|
Функции. Общие понятия
Функцией называется закон, в соответствии с которым каждому значению одной переменной (например, х) ставится в соответствие единственное значение другой переменной (например, у). Обозначения: y = f (x), y = y (x) и т.п. Множество Х значений аргумента х называют областью определения функции y = f (x), а множество Y значений у – областью значений функции y = f (x). Графиком функции y = f (x) на координатной плоскости х О у называется множество точек, имеющих координаты (х, f (x)), где х ÎХ.
Функция y = f (x) называется чётной, если f (- x) = f (x). График четной функции симметричен относительно оси О у.
Функция y = f (x) называется нечётной, если f (- x) = - f (x). График нечетной функции симметричен относительно начала координат.
Причем область определения чётной и нечётной функций симметрична относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
Функция y = f (x) называется периодической, если существует такое число Т > 0, что при всех х ÎХ значения х - Т и х+Т также принадлежат области определения Х, причем f (x - Т) = f (x+Т) = f (x). Наименьшее из таких Т, если оно существует, называется основным периодом функции.
Асимптотой графика функции называется прямая, к которой сколь угодно близко приближаются точки этого графика при неограниченном их удалении от начала координат.
Способы задания функции
1. Аналитический. Функцию в декартовой системе координат можно задать с помощью формулы, которую обычно записывают в виде 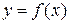 . При этом х называют аргументом функции.
. При этом х называют аргументом функции.
2. Табличный. Примером такого задания функций является любой статистический справочник.
3. Графический. Функцию можно задать с помощью некоторой кривой (являющейся, например, результатом какого-нибудь эксперимента) в некоторой системе координат.
|
|
|
Основные элементарные функции
Основными элементарными функциями называются следующие функции:
1.  – степенная функция. Область определения:
– степенная функция. Область определения:  .
.
2.  – показательная функция. Область определения: х Î R, а > 0, a ¹ 1
– показательная функция. Область определения: х Î R, а > 0, a ¹ 1
3.  – л огарифмическая функция Область определения: x > 0, а > 0, a ¹ 1.
– л огарифмическая функция Область определения: x > 0, а > 0, a ¹ 1.
4. Тригонометрические функции 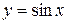 ,
,  ,
,  ,
,  .
.
5. Обратные тригонометрические функции  ,
,  ,
,  ,
,  .
.
Рассмотрим графики некоторых функций:
1. Линейная функция y = kx + b
(см. рис. 1). Область определения х Î R. k – угловой коэффициент, k = tga.
2. Квадратичная функция  , ,  . График – парабола. Координаты вершины параболы: . График – парабола. Координаты вершины параболы:
 , ,  .
Если .
Если 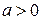 , то ветви параболы направлены вверх, если , то ветви параболы направлены вверх, если  , то ветви параболы направлены вниз.
Квадратное уравнение , то ветви параболы направлены вниз.
Квадратное уравнение
 . (1)
Имеет решение при условии, что дискриминант . (1)
Имеет решение при условии, что дискриминант  . Корни уравнения находятся по формуле . Корни уравнения находятся по формуле
 Теорема Виета:
Теорема Виета:

|
 
| |||
3. Обратная пропорциональность   . Область определения: х Î R, x ¹ 0. График – гипербола, асимптоты – оси координат. Нечетная функция (cм. рис. 5). . Область определения: х Î R, x ¹ 0. График – гипербола, асимптоты – оси координат. Нечетная функция (cм. рис. 5).
| 
| |||
4.Показательная функция  , а > 0, a ¹ 1. Область определения: х Î R. Область значений: у > 0. Асимптота: y = 0. График – экспонента (см. рис. 6). , а > 0, a ¹ 1. Область определения: х Î R. Область значений: у > 0. Асимптота: y = 0. График – экспонента (см. рис. 6).
| 
| |||
5.Логарифмическая функция  , а > 0, a ¹ 1. Область определения: x > 0. Асимптота: х = 0. (см. рис. 7) , а > 0, a ¹ 1. Область определения: x > 0. Асимптота: х = 0. (см. рис. 7)
| 
| |||
Тригонометрические и обратные тригонометрические функции
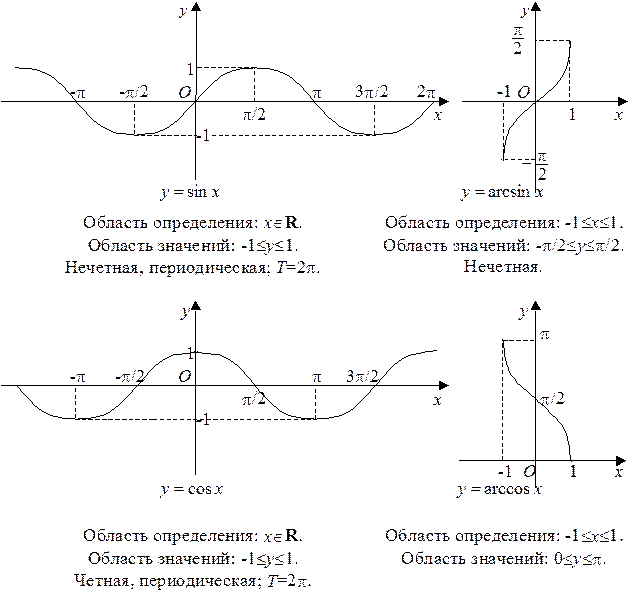


 Некоторые значения тригонометрических функций
Некоторые значения тригонометрических функций
Угол 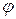 Фунция
Фунция
| 
| 
| 
| 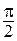
| 
| 
| 
| p | |
sin 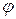
| 
| 
| 
| 
| 
| 
| |||
cos 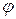
| 
| 
| 
| 
| 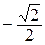
| 
| –1 | ||
tg 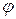
| 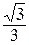
| 
| – | 
| –1 | 
| |||
ctg 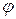
| – | 
| 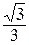
| 
| –1 | 
| – |
Элементарными называются функции, полученные путем арифметических действий над основными элементарными функциями и действием взятия функции от функции.
Например: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 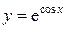 и т.д.
и т.д.
 , где
, где  промежуточный аргумент, то есть
промежуточный аргумент, то есть|
|
|
3)  , где
, где 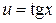 ; 4)
; 4)  , где
, где 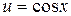
Пример
Проверить возможность междурядной обработки картофеля трактором МТЗ-80 при высоте растений 0,5 м и междурядьи посева b = 0,7 м. Найти защитные зоны у колес.
При движении трактора по центрам междурядий колея трактора  м, т.е. 1400 мм. Колея передних и задних колес МТЗ-80 с первым вариантом установленных шин регулируется в пределах 1250–1800 (2100 у задних) мм – по размеру колеи работа возможна.
м, т.е. 1400 мм. Колея передних и задних колес МТЗ-80 с первым вариантом установленных шин регулируется в пределах 1250–1800 (2100 у задних) мм – по размеру колеи работа возможна.
Агротехнический просвет МТЗ-80  мм, т.е. больше высоты растений – работа без повреждения растений возможна.
мм, т.е. больше высоты растений – работа без повреждения растений возможна.
Ширина шин задних колес МТЗ-80 (первый вариант) равна 12 дюймов, т.е.  мм. Защитная зона (расстояние до растений) у колес при их движении по центрам междурядий
мм. Защитная зона (расстояние до растений) у колес при их движении по центрам междурядий  мм (≈ 20 см) – работа возможна с уплотнением около 40% ширины междурядий, по которым движется трактор.
мм (≈ 20 см) – работа возможна с уплотнением около 40% ширины междурядий, по которым движется трактор.
|
|
|




