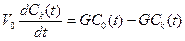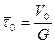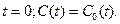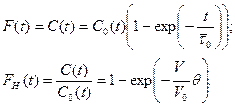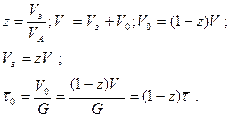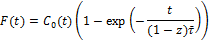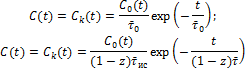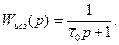Задание 1.1 - Разработка математических моделей гидродинамики
Исследование двух типовых моделей гидродинамики в соответствии с заданным вариантом задания.Приведите уравнения материального баланса и уравнения реакции объекта на типовые возмущения. Проведите вычислительный эксперимент. В среде MathCad получить таблицы и графики характеристик. Для заданной производительности определите рабочий объем аппарата. Исследование модели заключается в получении реакций модели на типовые возмущения (ступенчатое и импульсное) при варьировании параметров модели.
На основании полученных результатов сделайте вывод о влиянии варьируемых параметров на выходные характеристики.
Задания к контрольной работе 1.1 приведены в таблице 1.2, где используются следующие обозначения:
ИС - модель идеального смешения;
ИСП - модель идеального смешения с проскоком;
ИСЗ - модель идеального смешения с застойной зоной;
ИСПЗ- модель идеального смешения с проскоком и с застойной зоной;
ЯМ - ячеечная модель;
ОДМ - однопараметрическая диффузионная модель.
Таблица1.2- Варианты заданий для исследования ММ гидродинамики
|
| № варианта
| Тип
модели
| Время исследования,
t, мин
| Начальная
конц-я
индикатораC, моль/л
| Варьиру-емый параметр
|
Диапазон, шаг
| Производи-
тельность,
G л/мин
| Получить
|
| 1
| ЯМ
Время пребывания: τ =50 мин.
| 100
| 40
| количество ячеек, n
| n=2-11
с шагом dn=3
| 200
| 14
|
| ИСП
Время пребывания: τ =45 мин.
| 100
| 20
| Доля проскока, dm
| m=0-0.3
dm=0.1
| 200
| кривые разгона, импульс. х-ки
|
| 2
| ОДМ
Время пребывания: 40 мин.
| 60
| 40
| критерий Пекле, Pe
|
Pe от 200 до 600
С шагом 100
| 250
|
|
| ИСП
Время пребывания: τ =50 мин.
| 100
| 15
| Доля проскока, dm
| m=0-0.3
dm=0.1
| 200
| кривые разгона, импульс. х-ки
|
| 3
| ИСП
Время пребывания:
τ =40 мин.
| 100
| 20
| Доля проскока, dm
| m=0-0.3
dm=0.1
| 180
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =30 мин.
| 120
| 40
| количество ячеек, n
| n=2-11
с шагом dn=3
| 200
|
|
| 4
| ИСЗ
Время пребывания:
τ =20 мин.
| 80
| 30
| Доля застойной зоны, dz
| z=0-0.2
dz=0.1
| 300
| кривые разгона, импульс. х-ки
|
| 5
| ИСЗ
Время пребывания:
τ =45 мин.
| 100
| 20
| Доля застойной зоны, dz
| z=0-0.4
dz=0.1
| 300
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =20 мин.
| 80
| 20
| количество ячеек,n
| n=2-11
с шагом dn=3
|
|
|
| 6
| ИСЗ
Время пребывания:
τ =30 мин.
| 80
| 30
| Доля застойной зоны, dz
| z=0-0.3
dz=0.1
| 300
| кривые разгона, импульс. х-ки
|
|
| 60
| 40
| критерий Пекле, Pe
|
Pe от 200 до 600
С шагом 100
| 250
|
|
|
Продолжение таблицы 1.2
|
|
| № варианта
| Тип
модели
| Время исследования,
t, мин
| Начальная
конц-я
индикатораC, моль/л
|
Варьиру-емый параметр
| Диапазон, шаг
| Производитель-ность,
G л/мин
|
|
| 7
| ИС
| 100
| 20
| Время пребывания, τ
| τ= 10;30;50
| 200
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =45 мин.
| 80
| 30
|
Количество ячеек,n
| n=2-10
с шагом dn=2
|
|
|
| 8
| ИС
| 100
| 20
| Время пребывания, τ
| τ= 20;40;70
| 250
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =20 мин.
| 80
| 20
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
|
|
| 9
| ИСПЗ
Время пребывания: τ =30 мин.
| 100
| 30
|
Доля застойной зоны, z Доля проскока, m
| z=0-0.025
dz=0.05
m=0-0.3
dm=0.1
| 300
|
|
| ЯМ
Время пребывания: τ =30 мин.
| 120
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
|
|
| 10
| ИСПЗ
Время пребывания: τ =30 мин.
| 100
| 30
|
Доля застойной зоны, z Доля проскока, m
| z=0-0.025
dz=0.05
m=0-0.3
dm=0.1
| 300
|
|
| ОДМ
Время пребывания: 40 мин.
| 60
| 40
|
Критерий Пекле, Pe
| Pe от 200 до 600
С шагом 100
| 250
|
|
|
Продолжение таблицы 1.2
|
| № варианта
| Тип
модели
| Время исследования,
t, мин
| Начальная
конц-я
индикатораC, моль/л
|
Варьиру-емый параметр
| Диапазон, шаг
| Производитель-ность,
G л/мин
|
|
| 11
| ИСПЗ
Время пребывания: τ =30 мин
| 100
| 30
|
Доля застойной зоны, z Доля проскока, m
| z=0-0.3
dz=0.1
m=0-0.3
dm=0.1
| 300
| кривые разгона, импульс. х-ки
|
| ОДМ
Время пребывания: 40 мин.
| 60
| 40
|
Критерий Пекле, Pe
| Pe от 200 до 600
С шагом 100
| 250
|
|
| 12
| ИСПЗ
Время пребывания: τ =30 мин.
| 100
| 30
|
Доля застойной зоны, z Доля проскока, m
| z=0-0.025
dz=0.05
m=0-0.3
dm=0.1
| 300
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =20 мин.
| 80
| 20
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
| импульс. х-ки
|
| 13
| ЯМ
Время пребывания: τ =30 мин.
| 120
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
| импульс. х-ки
|
| ИС
| 100
| 20
| Время пребывания, τ
| τ= 10;30;50
| 200
|
|
| 14
| ЯМ
Время пребывания: τ =40 мин.
| 120
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
| импульс. х-ки
|
| ИСЗ
Время пребывания:
τ =40 мин.
| 90
| 30
|
Доля застойной зоны, dz
| z=0-0.2
dz=0.1
| 300
|
|
| 15
| ЯМ
Время пребывания: τ =50 мин.
| 100
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
| импульс. х-ки
|
| ИС
| 100
| 40
| Время пребывания, τ
| τ= 10;20;60
| 350
|
|
| 16
| ЯМ
Время пребывания: τ =45 мин.
| 80
| 30
|
Количество ячеек,n
| n=2-10
с шагом dn=2
| 300
| импульс. х-ки
|
| ИСП
Время пребывания: τ =50 мин.
| 100
| 15
|
Доля проскока,dz
| m=0-0.3
dm=0.1
| 200
|
|
|
Продолжение таблицы 1.2
|
|
| № варианта
| Тип
модели
| Время исследования,
t, мин
| Начальная
конц-я
индикатораC, моль/л
|
Варьиру-емый параметр
| Диапазон, шаг
| Производитель-ность,
G л/мин
|
|
| 17
| ИС
| 100
| 40
| Время пребывания, τ
| τ= 10;20;60
| 350
|
|
|
| ОДМ
Время пребывания: 40 мин.
| 60
| 40
|
Критерий Пекле, Pe
| Pe от 200 до 600
С шагом 100
| 250
| импульсные характеристики
|
| 18
| ОДМ
Время пребывания: 50 мин.
| 100
| 20
|
Критерий Пекле, Pe
| Pe от 100 до 500
С шагом 100
| 150
| импульсные характеристики
|
| ИС
| 100
| 20
| Время пребывания, τ
| τ= 10;30;50
| 200
|
|
| 19
| ИСЗ
Время пребывания:
τ =40 мин.
| 90
| 30
|
Доля застойной зоны, dz
| z=0-0.2
dz=0.1
| 300
| кривые разгона, импульс. х-ки
|
| ОДМ
Время пребывания: 40 мин.
| 60
| 40
|
Критерий Пекле, Pe
| Pe от 200 до 600
С шагом 100
| 250
|
|
| 20
| ИС
| 100
| 20
| Время пребывания, τ
| τ= 10;30;50
| 200
| кривые разгона, импульс. х-ки
|
| ЯМ
Время пребывания: τ =50 мин.
| 120
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
|
|
| 21
| ИС
| 100
| 40
| Время пребывания, τ
| τ= 10;20;60
| 350
| кривые разгона, импульс. х-ки
|
| ОДМ
Время пребывания: 60 мин.
| 60
| 40
|
Критерий Пекле, Pe
| Pe от 200 до 600
С шагом 100
| 250
|
|
| 22
| ИСЗ
Время пребывания:
τ =35 мин.
| 90
| 20
|
Доля застойной зоны, dz
| z=0-0.4
dz=0.1
| 300
|
|
| ЯМ
Время пребывания: τ =50 мин.
| 120
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 200
|
|
|
Продолжение таблицы1. 2
|
| № варианта
| Тип
модели
| Время исследования,
t, мин
| Начальная
конц-я
индикатораC, моль/л
|
Варьиру-емый параметр
| Диапазон, шаг
| Производитель-ность,
G л/мин
|
|
| 23
| ИСП
Время пребывания: τ =50 мин.
| 100
| 15
|
Доля проскока,dz
| m=0-0.3
dm=0.1
| 200
| кривые разгона, импульс. х-ки
|
| ОДМ
Время пребывания: 40 мин.
| 140
| 40
|
Критерий Пекле, Pe
| Pe от 100 до 500
С шагом 100
| 250
|
|
| 24
| ЯМ
Время пребывания: τ =50 мин.
| 120
| 60
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 250
|
|
| ИС
| 100
| 40
| Время пребывания, τ
| τ= 10;20;60
| 350
|
|
| 25
| ЯМ
Время пребывания: τ =30 мин.
| 100
| 40
|
Количество ячеек,n
| n=2-11
с шагом dn=3
| 300
| импульс. х-ки
|
| ИСПЗ
Время пребывания: τ =30 мин.
| 100
| 30
|
Доля застойной зоны, z Доля проскока, m
| z=0-0.025
dz=0.05
m=0-0.3
dm=0.1
|
|
|
| | | | | | | | | |
Получить с помощью пакета символьной математики MathCad кривые разгона (F-кривые) модели идеального смешения с застойной зоной при времени пребывания 30 мин, изменяя величину застойной зоны от 0 до 0,3 от объема реактора с шагом 0,1.
Для расчета характеристик задать следующие входные данные: начальная концентрация индикатора равна 20 моль/л, время исследования 80 мин.
Получить таблицы и графики характеристик. Для заданной производительности 200 л/мин определить рабочий объем аппарата.
Решение задачи с помощью MathCad показано на рисунках 1 и 2. Исходными данными являются: время пребывания (tau = 20 мин), доля проскока (значения заданы в соответствии с условием задачи: zmin = 0; zmax=0.3; dz = 0,1;), доля застойной зоны (z = 0), начальная концентрация индикатора (c0 = 30 моль/л), время исследования меняется от 0 до 80 мин с шагом 1 мин (при необходимости величину шага можно изменить).
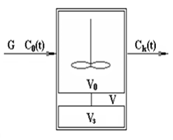
На рисунке 1.1 приведена схема модели аппарата ИС с застойной зоной. Застойная зона — это часть реактора с перемешивающим устройством, который может возникнуть при работе реальных аппаратов больших размеров, где наблюдается отсутствие обмена (или слабый обмен) вещества между основным объемом и объемом застойной зоны.
1. Уравнение материального баланса для модели ИСЗ.
Модель ИСЗ отличается от ИС значением параметра-времени пребывания.
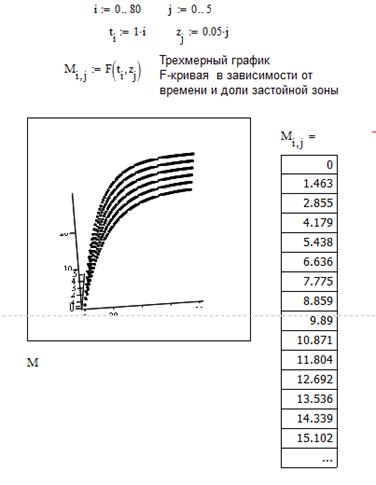
2. Кривая разгона (F-кривая) модели ИСЗ.
Обозначим через z — долю застойной зоны. Выразим параметры модели через z:
3. Импульсные характеристики (С-кривые) модели ИСЗ:
4. Передаточная функция модели ИСЗ.
С точки зрения динамических характеристик ИСЗ представляет собой инерционное звено первого порядка с меньшей, чем у ИС постоянной времени.



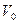 - рабочий объем аппарата, м3;
- рабочий объем аппарата, м3;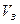 - объем застойной зоны, м3;
- объем застойной зоны, м3;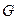 - объемный расход через аппарат, м3/ч.
- объемный расход через аппарат, м3/ч.