 |
Тема: Разработка математической модели выпарного аппарата
|
|
|
|
В выпарном аппарате происходят следующие физические процессы: конденсация пара в греющей камере, передача тепла от пара через стенку поверхности нагрева к кипящей жидкости, в результате чего выделяются пары растворителя и увеличивается концентрация раствора (рисунок 3.1).
Рисунок 3.1- Схема выпарного аппарата
Выпарные аппараты, как правило, представляют собой емкость с выпариваемым раствором, обогреваемую перегретым паром. Вторичный пар, образующийся при кипении раствора, отсасывается из верхней части аппарата вакуум-насосом; упаренный раствор отводится из нижней части аппарата. Необходимый для обеспечения теплопередачи от греющего пара к выпариваемому раствору перепад температуры получается вследствие того, что давление греющего пара выше, чем давление над кипящим раствором.
Входными переменными выпарного аппарата являются расход 
и концентрация 
раствора, подаваемого на вход; расход тепла 
, поступающего со свежим греющим паром (расход тепла для насыщенного пара однозначно определяется его температурой 
).
Рисунок 3.2 - Структурная схема выпарного аппарата
Выходные переменные - расход вторичного пара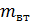 
, расход 
раствора на выходе и концентрация 
раствора на выходе. Наиболее важной выходной координатой для выпарных аппаратов является концентрация раствора на выходе. Формализованное описание приведено на рисунке 3.2.
Примем следующую систему допущений:
1. Гидродинамический режим - идеальное смешение.
2. Тепловые потери в окружающую среду отсутствуют.
3. В выпарной аппарат подается раствор, нагретый до температуры кипения.
4. Выпарной аппарат является стационарным объектом.
|
|
|
5. Теплоемкость раствора и теплота парообразования не зависят от температуры и концентрации раствора.
Целью построения ММ является получение уравнений, связывающих выходную координату с входными: , , .
ММ статики выпарного аппарата состоит из следующих уравнений:
- материального баланса:
; (1)
- материального баланса по сухому веществу:
; (2)
- теплового баланса (с учетом допущения 2):
, (3)
где 
- поток тепла через поверхность теплообмена от греющего пара к кипящему раствору, Дж/с; 
- поток тепла, вносимого в аппарат с раствором, Дж/с; 
- поток тепла, уходящего из аппарата с раствором, Дж/с; 
- поток тепла, уходящего из аппарата со вторичным паром, Дж/с.
Потоки тепла выражаются следующими зависимостями:
, (4)
где 
- коэффициент теплопередачи, Вт/м2×град;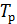 
- температура кипения раствора, °С; - температура греющего пара, °С; 
- площадь теплообмена, м2;
, (5)
где 
- теплоемкость раствора, Дж/кг×град; 
- температура раствора на входе, °С;
; (6)
, (7)
где 
- теплота парообразования вторичного пара, Дж/кг.
Учитывая допущение 3, уравнение (5) может быть записано в следующем виде:
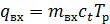. (8)
Подставив в уравнение (3) выражения (4), (6) - (8), получим:
(9)
Из уравнений (1), (2), (9) получить зависимость:
Эту зависимость предлагается найти самостоятельно.
Подготовить программу для вычислительной машины на любом языке программирования или в среде MathCad.
|
|
|
В работе требуется получить статические характеристики по каналам:
а) 
Концентрация изменяется от 
до 
с шагом 
. При этом 
, 
.
б) 
Расход на входе изменяется от 
до 
с шагом 
кг/с. При этом 
, .
в) 
Температура греющего пара изменяется от 
до 
с шагом 
°C. При этом , .
Содержание отчета о работе - графики зависимостей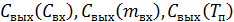 
.
Номер варианта соответствует двум последним цифрам номера зачетной книжки, то есть цифры 01 соответствуют номеру варианта 1, 02 - номеру варианта 2 и т.д. Если две последние цифры номера зачетной книжки - 51, то им соответствует также номер варианта 1, 52 - номер варианта 2 и т.д., вплоть до 99 - номер варианта 49, 00 - номер варианта 50 (таблица 1).
Исходные данные, необходимые для расчета, приведены в табл. 2, используемые константы - в табл. 3.
Таблица 3.1 - Задания
| № варианта | , %
| , %
| , %
| , кг/с
| , кг/с
| , кг/с
| , °С
| , °С
| , °С
|
| 1 | 14 | 18 | 15 | 4 | 6 | 5 | 120 | 135 | 130 |
| 2 | 6 | 10 | 8 | 4 | 6 | 4 | 122 | 140 | 130 |
| 3 | 8 | 12 | 10 | 4,5 | 6,8 | 5 | 125 | 140 | 135 |
| 4 | 9 | 14 | 12 | 4,2 | 6,5 | 4,5 | 123 | 138 | 132 |
| 5 | 12 | 16 | 14 | 4,2 | 6,4 | 4,6 | 130 | 150 | 140 |
| 6 | 7 | 12 | 10 | 3,9 | 5,4 | 4 | 125 | 145 | 138 |
| 7 | 10 | 14 | 12 | 4,5 | 7 | 5 | 130 | 155 | 150 |
| 8 | 11 | 15 | 13 | 4,8 | 7 | 6 | 132 | 160 | 153 |
| 9 | 20 | 25 | 20 | 6 | 8 | 7 | 120 | 140 | 130 |
| 10 | 13 | 18 | 16 | 5 | 7 | 6 | 124 | 142 | 135 |
| 11 | 6 | 12 | 9 | 3,8 | 5,4 | 4,2 | 120 | 140 | 130 |
| 12 | 15 | 20 | 16 | 4,4 | 6,9 | 4,8 | 132 | 158 | 146 |
| 13 | 8 | 14 | 12 | 5 | 7 | 6 | 128 | 145 | 140 |
| 14 | 18 | 23 | 21 | 7 | 8,4 | 7 | 150 | 160 | 155 |
| 15 | 17 | 21 | 18 | 4 | 6 | 5 | 130 | 140 | 136 |
| 16 | 7,5 | 12 | 8 | 3,8 | 5,5 | 4 | 125 | 140 | 140 |
| 17 | 19 | 24 | 22 | 6,3 | 8,8 | 6,5 | 140 | 152 | 150 |
| 18 | 14 | 20 | 15 | 7 | 8,5 | 7 | 142 | 158 | 152 |
| 19 | 7 | 10 | 8 | 3,9 | 5,7 | 4,8 | 133 | 145 | 142 |
| 20 | 10 | 15 | 12 | 4,6 | 7 | 5 | 135 | 150 | 145 |
| 21 | 14 | 20 | 19 | 4,8 | 6,6 | 4,9 | 120 | 140 | 135 |
| 22 | 5 | 9 | 6 | 4,8 | 7,5 | 5,2 | 130 | 150 | 140 |
| 23 | 12 | 17 | 14 | 4,1 | 6,9 | 4,2 | 128 | 144 | 142 |
| 24 | 13 | 19 | 16 | 5,2 | 7,7 | 5,5 | 141 | 156 | 148 |
| 25 | 11 | 15 | 13 | 4 | 6 | 4,5 | 132 | 146 | 140 |
Таблица 3.2 - Теплофизические константы
| Обозначение | Значение | Единица измерения |
| r | 2.26×106 | Дж/кг |
| к t | 5000 | Вт/м2×град |
| F | 10 | М2 |
| Tp | 90 | 0C |
| ct | 4187 | Дж/кг×град |
|
|
|
