 |
Статистические показатели социальной работы и методы их анализа
|
|
|
|
коэффициент корреляция ряд динамика
Тема «Статистические показатели социальной работы и методы их анализа» изучается на стыке сразу нескольких взаимосвязанных дисциплин. Для современного состояния науки характерен переход к глобальному рассмотрению проблем тематики «Статистические показатели социальной работы и методы их анализа» [2].
Вопросам исследования посвящено множество работ. В основном материал, изложенный в учебной литературе, носит общий характер, а в многочисленных монографиях по данной тематике рассмотрены более узкие вопросы проблемы «Статистические показатели социальной работы и методы их анализа». Однако, требуется учет современных условий при исследовании проблематики обозначенной темы.
Высокая значимость и недостаточная практическая разработанность проблемы «Статистические показатели социальной работы и методы их анализа» определяют несомненную новизну данного исследования.
Дальнейшее внимание к вопросу о проблеме «Статистические показатели социальной работы и методы их анализа» необходимо в целях более глубокого и обоснованного разрешения частных актуальных проблем тематики данного исследования [2].
Социальное обеспечение - это система учреждений и услуг по оказанию помощи в случае стихийных бедствий; при ограничении либо потере трудоспособности; в ситуациях, требующих внешней помощи; а также по оказанию услуг, смягчающих диспропорции в условиях жизни населения.
Социальная защищенность населения - это совокупность механизмов, предусмотренных законодательными и нормативными актами для сохранения доходов (или их части) отдельным лицам или семьям, которые их больше не имеют в связи с потерей трудоспособности из-за старости или инвалидности, болезни, беременности (материнства), безработицы, смерти кормильца семьи, а также для материальной поддержки многодетных и малообеспеченных групп населения, учащейся молодежи и др.
|
|
|
При определении размеров социальной помощи исходят как из потребностей населения, нуждающегося в поддержке, так и из реальных ресурсов, которыми располагает государство для этих целей на данном этапе экономического развития страны. Нормы социального обеспечения служат, как правило, индикаторами социальной политики государства.
Исходя из задач и направлений деятельности органов и учреждений социального обеспечения, в задачи статистического наблюдения входит сбор следующих сведений [3]:
§ размеры социальных выплат и их источники;
§ численность лиц, охватываемых социальным обеспечением по его видам;
§ средние размеры социальных пособий, приходящихся на их получателя.
В связи с разнообразием социальных выплат кратко рассмотрим статистику социальных услуг и социальную поддержку семьи.
Наряду с выплатой пенсий и пособий важным элементом федеральной системы социального обеспечения является социальное обслуживание престарелых, нетрудоспособных и семей с детьми.
В соответствии с Федеральными законами «Об основах социального обслуживания населения в Российской Федерации» и «О социальном обслуживании граждан пожилого возраста и инвалидов» предусматривается разработка государственных стандартов социального обслуживания населения, устанавливающих основные требования к объектам и качеству социальных услуг, порядку и условиям их оказания. Это потребует внесения определенных корректив в существующую информационную базу [3].
Круг оказываемых в настоящее время социальных услуг достаточно широк и обусловлен потребностями упомянутых контингентов населения в связи с их болезнью, инвалидностью, старостью, многодетностью. Остановимся в основном на тех социальных услугах, которые носят массовый характер и отражаются в статистической или административной (отраслевой) отчетности. Прежде всего это касается лиц пожилого возраста и инвалидов.
|
|
|
Престарелые и инвалиды, включая детей-инвалидов, получают комплекс социальных услуг во время их пребывания в домах-интернатах. Эти медико-социальные учреждения предназначены для постоянного проживания престарелых и инвалидов, нуждающихся в уходе, бытовом и медицинском обслуживании. В период пребывания в домах-интернатах им предоставляется жилье, питание, одежда, медицинская и лекарственная помощь, лечение, социально-бытовое обслуживание.
Статистическая отчетность о деятельности домов-интернатов для престарелых и инвалидов (взрослых и детей) позволяет установить их общее число, количество мест и численность проживающих в них лиц, в том числе находящихся на постоянном постельном режиме (формы № 2-собес «Отчет дома-интерната для престарелых и инвалидов» и № 3-собес «Отчет детского дома-интерната для инвалидов»). В отчетности имеются также сведения о численности лиц, состоящих на очереди для помещения в дома-интернаты для взрослых и в детские дома-интернаты [3].
Другой существенной услугой, оказываемой населению, является бесплатное содержание детей-сирот и детей, оставшихся без попечения родителей, в лечебно-профилактических и учебно-воспитательных учреждениях, а также в детских домах семейного типа.
Статистика социального обеспечения располагает данными об общем количестве интернатных учреждений, в том числе по их видам (дома ребенка, детские дома, школы-интернаты) и численности детей, находящихся в них; численности детей-сирот и детей, оставшихся без попечения родителей, состоящих на учете; численности детей и подростков, оставшихся без попечения родителей, из них - устроенных в отчетном году в дома ребенка, детские дома и школы-интернаты, находящихся под опекой (попечительством) и усыновленных, направленных в учебно-воспитательные и учебные заведения на условиях постоянного государственного обеспечения.
Объектом статистического наблюдения является также оказание такого вида социальной услуги, как обеспечение инвалидов транспортными средствами (форма № 1-собес «Транспорт для инвалидов») [3].
|
|
|
В настоящее время все большее распространение получает и такой вид социальных услуг, как социальная помощь на дому. Такая помощь оказывается престарелым и инвалидам, нуждающимся в посторонней помощи в связи с утратой способности к самообслуживанию.
К основным социально-бытовым услугам, оказываемым на дому, относятся: доставка на дом продуктов питания, обедов, товаров первой необходимости, лекарств; оплата жилищно-коммунальных и других бытовых услуг. Оказание такой помощи престарелым и инвалидам является функцией отделений социальной помощи на дому центров социального обслуживания. Эти центры предоставляют информацию о численности лиц, которым была предоставлена помощь на дому в отчетном периоде.
Общепризнано, что семья является важнейшим социальным институтом, в котором рождаются и воспитываются новые поколения. В соответствии с Законом о семье и браке, принятом в Российской Федерации в 1996 г., семейная политика провозглашена как одно из важных направлений социальной политики государства [3].
На уровне государства закреплены пути и формы поддержки семьи как фундаментального общественного института, обеспечение гарантированных форм материальной поддержки.
Для целей статистического анализа в этой области могут использоваться данные об основных социальных гарантиях, предоставляемых государством в виде единовременных пособий при рождении каждого ребенка, ежемесячного пособия на период отпуска по уходу за ребенком до достижения им возраста 1,5 лет, ежемесячного пособия на каждого ребенка до 16 лет, ежемесячных пособий на детей одиноким матерям и т.д. [3]
Сведения об общих фактических размерах пособий, носящих трансфертный характер, и их доле в доходах семьи содержатся в данных бюджетных обследований населения.
Задачи
Задание 1
. Произведите аналитическую группировку 20 предприятий по среднегодовой стоимости основных производственных фондов, образовав не более четырех групп с равными закрытыми интервалами.
|
|
|
. По каждой группе приведите структуру среднегодовой стоимости основных производственных фондов, а также определите средние абсолютные и относительные показатели - фондоотдачу и выработку на 1-го работающего.
. Составьте таблицу с системой абсолютных и относительных показателей и сделайте выводы.
Исходные данные представлены в таблице 2.
Таблица 2 - Показатели работы предприятий
| № предприятия | Валовая продукция (ВП), млрд. руб. | Среднегодовая стоимость основных производственных фондов (ОПФ), млрд. руб. | Среднегодовая численность ППП. (СЧППП) | Среднегодовой фонд заработной платы ППП. (ФЗПППП), тыс. руб. |
| 21 | 10,734 | 8,132 | 1512 | 28025 |
| 22 | 9,954 | 6,726 | 1143 | 20968 |
| 23 | 4,074 | 5,992 | 646 | 11049 |
| 24 | 24,688 | 10,734 | 2463 | 45893 |
| 25 | 70,226 | 51,260 | 4973 | 99400 |
| 26 | 8,125 | 5,381 | 1147 | 20719 |
| 27 | 11,559 | 8,083 | 1945 | 36813 |
| 28 | 10,814 | 5,942 | 1896 | 33956 |
| 29 | 9,684 | 3,696 | 918 | 17016 |
| 30 | 16,000 | 9,143 | 1748 | 34873 |
| 31 | 2,643 | 1,716 | 626 | 11237 |
| 32 | 6,140 | 2,729 | 881 | 17306 |
| 33 | 19,723 | 18,433 | 1766 | 39250 |
| 34 | 8,412 | 5,842 | 1034 | 19074 |
| 35 | 8,316 | 5,940 | 890 | 18452 |
| 36 | 6,502 | 4,963 | 840 | 17500 |
| 37 | 43,822 | 39,127 | 3262 | 7888 |
| 38 | 30,000 | 25,862 | 3116 | 58947 |
| 39 | 6,658 | 7,566 | 4646 | 94697 |
| 40 | 8,096 | 12,368 | 1383 | 29626 |
Решение:
Определяем величину равного интервала i:
(10)
где xmax, xmin - максимальное и минимальное значение группировочного признака в совокупности;- количество интервалов (групп).
Максимальное значение среднегодовой стоимости основных производственных фондов по данным таблицы 2 составляет 51,26 млрд. руб.
Минимальное значение среднегодовой стоимости основных производственных фондов по данным таблицы 2 составляет 1,716 млрд. руб.
По условию задачи необходимо образовать не более четырех групп с равными закрытыми интервалами. Таким образом, примем n = 4.
Величина равного интервала i составит:
млрд. руб.
Итак, равные закрытые интервалы составят:
1) 1,716 - 14,104
2) 14,102 - 26,488
) 26,488 - 38,874
) 38,874 - 51,26
Группировка предприятий по рассчитанным интервалам представлена в таблице 3.
Таблица 3 - Группировка предприятий по рассчитанным интервалам
| № группы | Интервал, млрд. руб. | Номера предприятий | Число предприятий |
| 1 | 1,716 - 14,104 | 21-24, 26-32, 34-36, 39-40 | 16 |
| 2 | 14,102 - 26,488 | 33, 38 | 2 |
| 3 | 26,488 - 38,874 | - | 0 |
| 4 | 38,874 - 51,26 | 25, 37 | 2 |
| Итого | 20 | ||
Итак, по данным таблицы 3 видно, что имеется пустой интервал - от 26,488 до 38,874 млрд. руб.
Следовательно, необходимо укрупнить интервалы, уменьшив количество групп.
Примем n = 3.
Величина равного интервала i составит:
млрд. руб.
Итак, равные закрытые интервалы составят:
1) 1,716 - 18,226
2) 18,226 - 34,736
) 34,736 - 51,26
Группировка предприятий по рассчитанным интервалам представлена в таблице 4.
|
|
|
Таблица 4 - Группировка предприятий по рассчитанным интервалам
| № группы | Интервал, млрд. руб. | Номера предприятий | Число предприятий |
| 1 | 1,716 - 18,226 | 21-24, 26-32, 34-36, 39-40 | 16 |
| 2 | 18,226 - 34,736 | 33, 38 | 2 |
| 3 | 34,736 - 51,26 | 25, 37 | 2 |
| Итого | 20 | ||
Итак, пустых интервалов в данной группировке нет, следовательно, можно продолжить расчеты.
Среднегодовая стоимость основных производственных фондов в среднем на один завод рассчитывается по формуле:
(11)
где ОПФ - среднегодовая стоимость основных производственных фондов по группе заводов, n - количество заводов в группе.
Фондоотдача рассчитывается по формуле:
(12)
где В - стоимость валовой продукции.
Для определения выработки на одного работающего количество произведенной продукции делится на численность всего персонала:
(13)
где Ч - численность всего персонала.
Структура среднегодовой стоимости основных производственных фондов, а также средние абсолютные и относительные показатели - фондоотдача и выработка на 1-го работающего, по каждой группе предприятий представлены в таблице 5.
Таблица 5 - Итоговая таблица
| № группы | Количество предприятий | Среднегодовая стоимость основных производственных фондов, млрд. руб. | Валовая продукция (ВП), млрд. руб. | Среднегодовая численность ППП. (СЧППП) | Среднегодовой фонд заработной платы ППП. (ФЗПППП), тыс. руб. | Фондоотдача | Выработка на 1-го работающего, млн. руб. | ||||
| Всего по группе | На 1 предпр. | Всего по группе | На 1 предпр. | Всего по группе | На 1 предпр. | Всего по группе | На 1 предпр. | ||||
| 1 | 16 | 104,953 | 6,56 | 152,399 | 9,52 | 23718 | 1482 | 457204 | 28575 | 1,45 | 6,43 |
| 2 | 2 | 44,295 | 22,15 | 49,723 | 24,86 | 4882 | 2441 | 98197 | 49099 | 1,12 | 10,18 |
| 3 | 2 | 90,387 | 45,19 | 114,048 | 57,02 | 8235 | 4118 | 107288 | 53644 | 1,26 | 13,85 |
| Итого | 20 | 239,635 | - | 316,17 | - | 36835 | - | 662689 | - | - | - |
Итак, по данным таблицы 5 можно сделать следующие выводы:
Наибольшая по числу предприятий группа № 1. В данной группе в совокупности произведено больше всего валовой продукции, однако выпуск валовой продукции на одно предприятие составляет всего 9,52 млрд. руб., данный показатель значительно меньше аналогичного показателя по остальным группам.
Наибольший выпуск валовой продукции в расчете на одно предприятие наблюдается в группе № 3 и составляет 57,02 млрд. руб.
Наибольшая среднегодовая численность персонала в расчете на одно предприятие соответствует группе № 3, наименьшая - группе № 1.
Наибольший показатель фондоотдачи соответствует группе № 1, наименьший - группе № 2.
Наибольшая выработка на 1-ого работающего наблюдается в группе № 3, наименьшая - в группе № 1.
Задание 2
. Постройте секционные диаграммы для двух фирм по дискретным вариационным рядам.
. Сделайте выводы об эффективности работы этих фирм и акции какой фирмы вы бы приобрели. Обоснуйте ваш выбор.
. Определите коэффициенты, обратные коэффициентам вариации по каждой фирме. Сравните ваши выводы с полученными коэффициентами и дайте интерпретацию этим коэффициентам.
Исходные данные представлены в таблице 6.
Таблица 6 - Годовая норма прибыли (%)
| Фирмы | Годы | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 15 | 13 | -17 | 16 | 18 | 11 | -7 | -9 | 5 | 13 |
| 2 | -7 | 12 | -9 | 28 | 35 | 15 | 15 | 15 | 19 | 25 |
Решение:
Определим Q1 для первой фирмы:
Так как n*q - дробное число, то принимаем n*q =2, тогда:
(14)
где x3 означает, что в ранжируемом дискретном ряду нижний квартиль по счету от минимального значения дискретного ранжированного ряда стоит на третьем месте, т. е. Q1 = 11.
Определим Q1 для второй фирмы:
Так как n*q - дробное число, то принимаем n*q =2, тогда:
где x3 означает, что в ранжируемом дискретном ряду нижний квартиль по счету от минимального значения дискретного ранжированного ряда стоит на третьем месте, т. е. Q1 = 15.
Определим Q2 для первой фирмы:
Так как n*q - целое число, то используем формулу:
(15)
т.е. Q2 = 14,5
Определим Q2 для второй фирмы:
Так как n*q - целое число, то используем формулу (14):
т.е. Q2 = 25
Определим Q3 для первой фирмы:
Так как n*q - дробное число, то принимаем n*q = 7, тогда:
где x8 означает, что в ранжируемом дискретном ряду верхний квартиль по счету от минимального значения дискретного ранжированного ряда стоит на восьмом месте, т. е. Q3 = 15.
Определим Q3 для второй фирмы:
Так как n*q - дробное число, то принимаем n*q = 7, тогда:
где x8 означает, что в ранжируемом дискретном ряду верхний квартиль по счету от минимального значения дискретного ранжированного ряда стоит на восьмом месте, т. е. Q3 = 25.
Секционные диаграммы для фирм № 1 и № 2 представлены на рисунках 1-2.
Рисунок 1 - Секционная диаграмма для фирмы № 1
Рисунок 2 - Секционная диаграмма для фирмы № 2
Для характеристики меры колеблемости в относительных величинах используют коэффициент вариации, определяемый по формуле 
, где S - стандартное отклонение (среднее квадратическое отклонение); x - среднее значение признака.
Среднее значение признака для первой фирмы составляет 5,8, для второй фирмы - 14,8.
Для первой фирмы стандартное отклонение составляет:
Для второй фирмы стандартное отклонение составляет:
Таким образом, коэффициент вариации для первой фирмы составит:
Коэффициент вариации для второй фирмы составит:
Рассчитанные коэффициенты вариации говорят о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.
Задание 3
. Определите взаимосвязь между среднегодовой стоимостью основных производственных фондов (факторный признак x) и выработкой на 1-го работающего (результативный признак y), рассчитав коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Исходные данные представлены в задаче 1, в итоговой таблице 5.
Перепишем, полученную в задаче 1 сгруппированную таблицу, по необходимым нам данным (таблица 7):
Таблица 7 - Исходные данные
| № группы | Количество предприятий | Среднегодовая стоимость основных производственных фондов, млрд. руб. | Выработка на 1-го работающего, млн. руб. |
| 1 | 16 | 104,953 | 6,43 |
| 2 | 2 | 44,295 | 10,18 |
| 3 | 2 | 90,387 | 13,85 |
| Итого | 20 | 239,635 | - |
Коэффициент детерминации вычисляется по формуле:
(16)
где 
- межгрупповая дисперсия,
- общая дисперсия.
Межгрупповая дисперсия рассчитывается по формуле:
(17)
где mJ - количество единиц в j группе.
Общая дисперсия рассчитывается по формуле:
(18)
Эмпирическое корреляционное отношение определяется по формуле:
(19)
Определим среднюю выработку на 1-ого работающего:
млрд. руб.
Строим расчетную таблицу:
Таблица 8 - Расчетная таблица
| № группы | Группировка предприятий по среднегодовой стоимости основных производственных фондов, млрд. руб. | Количество предприятий, n | Выработка на 1-го работающего, млн. руб. |   
| ||
| 1 | 1,716 - 18,226 | 16 | 6,43 | -1,12 | 1,25 | 19,96 |
| 2 | 18,226 - 34,736 | 2 | 10,18 | 2,63 | 6,93 | 13,87 |
| 3 | 34,736 - 51,26 | 2 | 13,85 | 6,30 | 39,73 | 79,46 |
| Итого | 20 | - | 7,82 | 47,91 | 113,28 |
Рассчитаем межгрупповую дисперсию по формуле 17:
Рассчитаем общую дисперсию по формуле 18:
Тогда коэффициент детерминации составит:
Коэффициент детерминации показывает, что среднегодовая стоимость ОПФ на 64% зависит от выработки на одного работающего и на 36% от неучтенных факторов.
Рассчитаем эмпирическое корреляционное отношение по формуле 19:
Это говорит о том, что связь между факторным и результативным признаками очень тесная, т.е. это свидетельствует о существенном влиянии на среднегодовую стоимость ОПФ выработки на одного работающего.
Задание 4
. Произведите 25% механический отбор предприятий (объем генеральной совокупности N = 20).
. По отобранным данным рассчитайте среднегодовой фонд заработной платы.
. С вероятностью 0.954 определите границы среднего фонда заработной платы для всех 20 предприятий.
Исходные данные представлены в таблице 9.
Таблица 9 - Показатели работы предприятий
| № предприятия | Валовая продукция (ВП), млрд. руб. | Среднегодовая стоимость основных производственных фондов (ОПФ), млрд. руб. | Среднегодовая численность ППП. (СЧППП) | Среднегодовой фонд заработной платы ППП. (ФЗПППП), тыс. руб. |
| 21 | 10,734 | 8,132 | 1512 | 28025 |
| 22 | 9,954 | 6,726 | 1143 | 20968 |
| 23 | 4,074 | 5,992 | 646 | 11049 |
| 24 | 24,688 | 10,734 | 2463 | 45893 |
| 25 | 70,226 | 51,260 | 4973 | 99400 |
| 26 | 8,125 | 5,381 | 1147 | 20719 |
| 27 | 11,559 | 8,083 | 1945 | 36813 |
| 28 | 10,814 | 5,942 | 1896 | 33956 |
| 29 | 9,684 | 3,696 | 918 | 17016 |
| 30 | 16,000 | 9,143 | 1748 | 34873 |
| 31 | 2,643 | 1,716 | 626 | 11237 |
| 32 | 6,140 | 2,729 | 881 | 17306 |
| 33 | 19,723 | 18,433 | 1766 | 39250 |
| 34 | 8,412 | 5,842 | 1034 | 19074 |
| 35 | 8,316 | 5,940 | 890 | 18452 |
| 36 | 6,502 | 4,963 | 840 | 17500 |
| 37 | 43,822 | 39,127 | 3262 | 7888 |
| 38 | 30,000 | 25,862 | 3116 | 58947 |
| 39 | 6,658 | 7,566 | 4646 | 94697 |
| 40 | 8,096 | 12,368 | 1383 | 29626 |
Решение:
Расстояние между отбираемыми единицами определяется делением численности генеральной совокупности (N) на численность выборочной совокупности (n).
Численность выборочной совокупности в данном случае составит:
единиц
В выборочную совокупность будут отобраны каждая четвертая единица генеральной совокупности (1:0,25=4).
Таким образом, можно организовать пять групп (20:4=5) с численностью в каждой группе по четыре единицы.
Так как генеральная совокупность упорядочена по нейтральному признаку, то в выборку может быть взята из группы любая единица, но для соблюдения принципа случайного отбора во всех последующих группах берутся те же единицы, которые соответствуют порядковому номеру первой группы.
Итак, берем каждое второе предприятие в группе, т.е. предприятия № 22, 26, 30, 34, 38. Результаты выборки представлены в таблице 10.
Таблица 10 - Результаты выборки
| № предприятия | Валовая продукция (ВП), млрд. руб. | Среднегодовая стоимость основных производственных фондов (ОПФ), млрд. руб. | Среднегодовая численность ППП. (СЧППП) | Среднегодовой фонд заработной платы ППП. (ФЗПППП), тыс. руб. |
| 22 | 9,954 | 6,726 | 1143 | 20968 |
| 26 | 8,125 | 5,381 | 1147 | 20719 |
| 30 | 16,000 | 9,143 | 1748 | 34873 |
| 34 | 8,412 | 5,842 | 1034 | 19074 |
| 38 | 30,000 | 25,862 | 3116 | 58947 |
Среднегодовой фонд заработной платы по отобранным предприятиям рассчитаем по формуле средней арифметической:
(20)
Итак, среднегодовой фонд заработной платы по отобранным предприятиям составит:
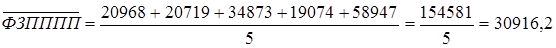тыс. руб.
Выборка при n < 30 называются малой выборкой и ее характеристики определяются по формулам 12-13:
(21)
(22)
Итак, рассчитаем дисперсию для выборочной совокупности:
Тогда, средняя ошибка выборки составит:
Предельная ошибка выборки определяется по формуле:
(23)
Так вероятность равна 0,954, то коэффициент доверия t равен 2,776 (по таблице значений критерия Стьюдента (t-критерия), с вероятностью 0,954 и числом степеней свободы v=n-1=5-1=4), следовательно, предельная ошибка выборки составит:
Доверительные интервалы (пределы) средней рассчитываем, исходя из двойного неравенства:
(24)
Таким образом, доверительные интервалы составят:
Таким образом, с вероятностью 0,954 можно утверждать, что средний фонд заработной платы лежит в границах от 10700 тыс. руб. до 51132,4 тыс. руб.
Задание 5
. Произведите сглаживание скользящей средней и центрирование.
. Определите индивидуальные индексы сезонности.
. Очистите исходный ряд динамики от сезонной составляющей и опишите полученный ряд динамики как функцию времени Tr = f (t).
. Вычислите ретроспективный и перспективный прогнозы на 4-й год по кварталам и интервал в котором будет находится прогнозная величина в IV квартале 4-го года.
. Фактические и расчетные данные изобразите графически.
Исходные данные представлены в таблице 11.
Таблица 11 - Исходные данные
| 1 год | 2 год | 3 год | |||||||||
| кварталы | кварталы | кварталы | |||||||||
| I | II | III | IV | I | II | III | IV | I | II | III | IV |
| 300 | 230 | 120 | 270 | 310 | 300 | 150 | 290 | 320 | 310 | 160 | 300 |
Решение:
Для выравнивания ряда используем линейную трендовую модель - уравнение прямой:
(25)
Параметры искомого уравнения прямой определяем из следующей системы нормальных уравнений:
(26)
(27)
откуда:
Уравнение прямой будет иметь вид:
Подставляя в данное уравнение последовательно значения t, равные -6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6, находим выровненные уровни 
.
Если 
, в нашем примере эти суммы равны между собой и равны 3060, следовательно, значения уровней выровненного ряда найдены верно.
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения выпуска продукции в среднем на 2,03 млн. руб. в месяц.
Расчетные данные представлены в таблице 12.
Таблица 12 - Расчетные значения
| Год | Квартал | Значение | Расчетные значения | |||
| t | t2 | y*t | 
| |||
| 1 год | I | 300 | -6 | 36 | -1800 | 242,82 |
| II | 230 | -5 | 25 | -1150 | 244,85 | |
| III | 120 | -4 | 16 | -480 | 246,88 | |
| IV | 270 | -3 | 9 | -810 | 248,91 | |
| 2 год | I | 310 | -2 | 4 | -620 | 250,94 |
| II | 300 | -1 | 1 | -300 | 252,97 | |
| III | 150 | 1 | 1 | 150 | 257,03 | |
| IV | 290 | 2 | 4 | 580 | 259,06 | |
| 3 год | I | 320 | 3 | 9 | 960 | 261,09 |
| II | 310 | 4 | 16 | 1240 | 263,12 | |
| III | 160 | 5 | 25 | 800 | 265,15 | |
| IV | 300 | 6 | 36 | 1800 | 267,18 | |
| Итого | 3060 | 0 | 182 | 370 | 3060 | |
Индивидуальный индекс сезонности можно рассчитать по формуле:
(28)
Индивидуальные индексы сезонности представлены в таблице 13.
Таблица 13 - Расчет индивидуальных индексов сезонности
| Год | Квартал | Значение | Расчетные значения | 
| |||
| t | t2 | y*t | 
| ||||
| 1 год | I | 300 | -6 | 36 | -1800 | 242,82 | 123,5 |
| II | 230 | -5 | 25 | -1150 | 244,85 | 93,9 | |
| III | 120 | -4 | 16 | -480 | 246,88 | 48,6 | |
| IV | 270 | -3 | 9 | -810 | 248,91 | 108,5 | |
| 2 год | I | 310 | -2 | 4 | -620 | 250,94 | 123,5 |
| II | 300 | -1 | 1 | -300 | 252,97 | 118,6 | |
| III | 150 | 1 | 1 | 150 | 257,03 | 58,4 | |
| IV | 290 | 2 | 4 | 580 | 259,06 | 111,9 | |
| 3 год | I | 320 | 3 | 9 | 960 | 261,09 | 122,6 |
| II | 310 | 4 | 16 | 1240 | 263,12 | 117,8 | |
| III | 160 | 5 | 25 | 800 | 265,15 | 60,3 | |
| IV | 300 | 6 | 36 | 1800 | 267,18 | 112,3 | |
| Итого | 3060 | 0 | 182 | 370 | 3060 | ||
Для устранения воздействия случайных факторов проведем усреднение индивидуальных индексов сезонности по кварталам. Используем формулу переменной средней:
По первому кварталу:
%
По второму кварталу:
%
По третьему кварталу:
%
По четвертому кварталу:
%
Вычисленные и откорректированные средние индексы сезонности составляют модель сезонности волны объемов выпуска продукции во внутригодовом цикле. Модель отражает квартальные колебания уровней.
Наибольшие объемы выпуска продукции ежегодно приходятся на I, ΙΙ и ΙΙV кварталы, снижение объемов - в ΙII квартале.
Определяем скорректированные индексы сезонности:
По первому кварталу:
По второму кварталу:
По третьему кварталу:
По четвертому кварталу:
Очищаем исходный ряд динамики от сезонной составляющей и получаем тренд:
(29)
Результаты расчета теоретического значения тренда представлены в таблице 14.
Таблица 14 - Результаты расчета теоретического значения тренда
| Год | Квартал | Значение | Расчетные значения |  
| ||||
| t | t2 | y*t | 
| |||||
| 1 год | I | 300 | -6 | 36 | -1800 | 242,82 | 123,5 | 225,56 |
| II | 230 | -5 | 25 | -1150 | 244,85 | 93,9 | 172,93 | |
| III | 120 | -4 | 16 | -480 | 246,88 | 48,6 | 90,23 | |
| IV | 270 | -3 | 9 | -810 | 248,91 | 108,5 | 203,01 | |
| 2 год | I | 310 | -2 | 4 | -620 | 250,94 | 123,5 | 233,08 |
| II | 300 | -1 | 1 | -300 | 252,97 | 118,6 | 225,56 | |
| III | 150 | 1 | 1 | 150 | 257,03 | 58,4 | 112,78 | |
| IV | 290 | 2 | 4 | 580 | 259,06 | 111,9 | 218,05 | |
| 3 год | I | 320 | 3 | 9 | 960 | 261,09 | 122,6 | 240,60 |
| II | 310 | 4 | 16 | 1240 | 263,12 | 117,8 | 233,08 | |
| III | 160 | 5 | 25 | 800 | 265,15 | 60,3 | 120,30 | |
| IV | 300 | 6 | 36 | 1800 | 267,18 | 112,3 | 225,56 | |
| Итого | 3060 | 0 | 182 | |||||
|
|
|
|||||||
