 |
Краткие теоретические сведения
|
|
|
|
В электрической цепи синусоидального тока с активным сопротивлением R (таблица 3.1) под действием синусоидального напряжения u = U msin ωt возникает синусоидальный ток i = I msin ωt, совпадающий по фазе с напряжением, так как начальные фазы напряжения U и тока I равны нулю (ψ u = 0, ψ i = 0). При этом угол сдвига фаз между напряжением и током φ = ψ u – ψ i = 0, что свидетельствует о том, что для этой цепи зависимости изменения напряжения и тока совпадают между собой на линейной диаграмме во времени.
Полное сопротивление цепи вычисляется по закону Ома
Z =  = R. (3.1)
= R. (3.1)
В электрической цепи синусоидального тока, содержащей катушку с индуктивностью L (таблица 3.1), под действием изменяющегося по синусоидальному закону напряжения u = U m sin(ωt + p/2) возникает синусоидальный ток i = I msin ωt, отстающий по фазе от напряжения на угол p/2.
При этом начальная фаза напряжения ψ u = p/2, а начальная фаза тока ψ i = 0. Угол сдвига фаз между напряжением и током φ = (ψ u – ψ i) = p/2.
В электрической цепи синусоидального тока с конденсатором, обладающим емкостью С (таблица 3.1), под действием напряжения u = U msin(ωt – p/2) возникает синусоидальный ток i = I msin ωt, опережающий напряжение на конденсаторе на угол p/2.
Начальный фазовый угол тока ψ i = 0, а напряжения ψ u = - p/2. Угол сдвига фаз между напряжением U и током I φ = (ψ u - ψ i) = - p/2.
В электрической цепи с последовательным соединением активного сопротивления R и катушки индуктивности L ток отстает от напряжения на угол φ › 0. При этом полное сопротивление цепи:
Z =  . (3.2)
. (3.2)
Проводимость цепи
Y =  , (3.3)
, (3.3)
где G = R/Z 2 – активная проводимость цепи;
B L = XL/Z 2 – реактивная индуктивная проводимость цепи.
Угол сдвига фаз между напряжением и током:
|
|
|
φ = arctg X L/ R = arctg B L/ G. (3.4)
Аналогично можно получить соответствующие расчетные формулы для электрических цепей синусоидального тока с различным сочетанием элементов R, L и C, которые даны в таблице 3.1.
При параллельном соединении сопротивлений параллельные ветви электрической цепи находятся под одним и тем же напряжением U = U 12, поэтому для каждой из этих ветвей определение всех расчетных величин производится по формулам, справедливым для отдельных сопротивлений электрических цепей с последовательным соединением сопротивлений. Для участка цепи с параллельным соединением сопротивлений ток на разветвленном участке определяется в соответствии с первым законом Кирхгофа, записанным для узла разветвления в векторной форме
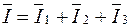 . (3.5)
. (3.5)
Этот ток можно определить графически с помощью векторной диаграммы, как сумму составляющих векторов токов.
Токи в отдельных ветвях электрической цепи могут быть определены через проводимости (y) соответствующих ветвей
I 1 = U 12× y 1; I 2 = U 12× y 2; I 3 = U 12× y 3. (3.6)
При этом ток в неразветвленной части цепи равен произведению напряжения U 12 на параллельном участке цепи на сумму проводимостей параллельно включенных сопротивлений
I = U 12×(y 1 + y 2 + y 3). (3.7)
Сопротивления отдельных ветвей могут носить активно-реактивный характер при наличии индуктивных ХL и емкостных Х C сопротивлений, поэтому в общем случае сопротивления могут быть определены через активные g и реактивные b проводимости
 (3.8)
(3.8)
При этом активные и реактивные проводимости:
 (3.9)
(3.9)
Мощность цепи с активным, индуктивным и емкостным сопротивлениями (R, L и C):
S = 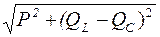 , (3.10)
, (3.10)
где P = I 2 R – активная мощность,
Q L = I 2 X L – индуктивная составляющая реактивной мощности,
Q С = I 2 X С – емкостная составляющая реактивной мощности.
В неразветвленной электрической цепи синусоидального тока с индуктивностью L, емкостью C и активным сопротивлением при определенных условиях может возникнуть резонанс напряжений (особое состояние электрической цепи, при которой ее реактивное индуктивное сопротивление XL оказывается равным реактивному емкостному XС сопротивлению цепи). Таким образом, резонанс напряжений наступает при равенстве реактивных сопротивлений цепи, т.е. при XL = XС.
|
|
|
Сопротивление цепи при резонансе Z = R, т.е. полное сопротивление цепи при резонансе напряжений имеет минимальное значение, равное активному сопротивлению цепи.
Угол сдвига фаз между напряжением и током при резонансе напряжений:
φ = ψu – ψi = arctg  = 0,
= 0,
при этом ток и напряжение совпадают по фазе. Коэффициент мощности цепи имеет максимальное значение: cos φ = R/Z = 1 и ток в цепи также приобретает максимальное значение I = U/Z = U/R.
Реактивная мощность цепи при резонансе напряжений:
Q = Q L - Q C = I 2 X L – I 2 X С = 0.
Активная мощность цепи при резонансе приобретает наибольшее значение, равное полной мощности
Р = UI ∙cos φ = S.
При построении векторной диаграммы для электрической цепи с последовательным включением сопротивлений исходным является ток 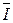 , так как в этом случае значение тока на всех участках цепи одинаково.
, так как в этом случае значение тока на всех участках цепи одинаково.
Ток 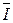 откладывается в соответствующем масштабе (mi = n А/см), затем относительно тока в принятом масштабе (mu = n В/см) откладывают падения напряжения ΔU на соответствующих сопротивлениях в последовательности их расположения в цепи и напряжение
откладывается в соответствующем масштабе (mi = n А/см), затем относительно тока в принятом масштабе (mu = n В/см) откладывают падения напряжения ΔU на соответствующих сопротивлениях в последовательности их расположения в цепи и напряжение 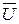 (рисунок 3.1).
(рисунок 3.1).

Рисунок 2.1 Построение векторной диаграммы
Таблица 3.1 Расчетные формулы для электрических цепей с различным сочетанием элементов R, L и C
| Элементы цепи | Условное изображение на схемах | Сопротивление, Ом | Проводимость, См | Угол сдвига фаз между напряжением и током, рад | Мощность | Векторная диаграмма | ||||
| Резистор R | 
| R | G= 1/ R | j = 0 | S = P = I 2 R |
 
 
| ||||
| Катушка индуктивности L (R к = 0) | 
| XL = w L | BL= 1/w L | j = p/2 | S = QL = I 2 XL P = 0, QС = 0 |  
 
| ||||
| Конденсатор C | 
| XL = 1/w C | BL= w C | j = –p/2 | S = QС = I 2 XС P = 0, QL = 0 |

  
| ||||
| Резистор и катушка индук-тивности RL | 
|
 Z= Ö R 2+ XL 2 Z= Ö R 2+ XL 2
| Y=R /(R2+XL 2) | j = arctg(XL / R) |  S = Ö P 2+ QL 2
S = UI
S = Ö P 2+ QL 2
S = UI
|   
| ||||
| Резистор и конденсатор RC | 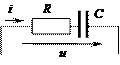   
|
 Z= Ö R 2+ XC 2 Z= Ö R 2+ XC 2
| Y=R /(R2+XC 2) | j = arctg(XC / R) |  S = Ö P 2+ QC 2
S = UI
S = Ö P 2+ QC 2
S = UI
|  
| ||||
| Резистор, катушка индук-тивности и кон-денсатор RLC | 
|
 Z= Ö R 2+(XL – XC)2
Z= Ö R 2+(XL – XC)2
| Y= R /(R2+ (XL–XC)2) | j = arctg(XL–XC)/ R |
 S = Ö P 2+(QL–QC)2
S = UI S = Ö P 2+(QL–QC)2
S = UI
| 
|
|
|
|
При смешанном соединении сопротивлений электрическая цепь при расчете приводится к виду, показанному на рисунке 3.3. Полное сопротивление Z 12 участка цепи 1-2 может быть определено через ее проводимость Z 12 = 1/ y 12. При этом расчет электрической цепи со смешанным соединением сопротивлений сводится к расчету простейшей электрической цепи с последовательным соединением сопротивлений.

Рисунок 3.3 Электрическая цепь после преобразования
При параллельном и смешанном соединении сопротивлений векторную диаграмму строят, начиная с вектора напряжения U 12 на параллельном участке цепи.
Задание № 2
Используя данные, приведенные в таблице 3.2 для электрической цепи переменного тока (рисунок 3.4), для своего варианта определить напряжение U, действующее на зажимах цепи, показание ваттметра PW1, емкость конденсатора С2 при резонансе токов, если на участке 1-2 электрической цепи амперметр PA1 показывает ток 6 А, а частота токи питающей сети f = 50 Гц. Построить векторную диаграмму токов и напряжений для всей электрической цепи.
Дополнительное задание: Определить активное R, реактивное X и полное Z сопротивления и соответствующие проводимости g, b, y, а также коэффициенты мощности cosφ, полную S, активную Р и реактивную Q мощности ветвей и всей электрической цепи.
Таблица 3.2 Данные для выполнения контрольного задания
| Вари- анты | Величины, Ом | Вари-анты | Величины, Ом | ||||||||
| R 1 | R 2 | X L1 | X L2 | X C2 | R 1 | R 2 | X L1 | X L2 | X C2 | ||
| 1,5 | 1,5 | ||||||||||
| 1,5 | 2,5 | ||||||||||
|
|
|

Рисунок 3.4 Схема электрической цепи
|
|
|



