Краткие теоретические сведения

ИССЛЕДОВАНИЕ ЭЛЕКТРОМАГНИТНОЙ

ОБСТАНОВКИ В АУДИТОРИИ

 

 

Методические указания

 

к лабораторной работе по дисциплине

«ЭЛЕКТРОМАГНИТНАЯ СОВМЕСТИМОСТЬ

РАДИОЭЛЕКТРОННЫХ СРЕДСТВ»

для студентов радиотехнических специальностей всех форм обучения

 

 

Минск 2015

 

СОДЕРЖАНИЕ

 

1. Цель работы……………………………………………………………………
2. Краткие теоретические сведения……………………………………………..
3.Определение плотности распределения и параметров случайных величин……………………………………………………………………………
4. Измерение параметров непреднамеренных помех………………………….
4.1 Общие сведения об измерении параметров помех…………………...
4.2 Многофункциональный радиоприемник AR5000……………………….
5. Подготовка к работе радиоприемника AR5000 и работа с ним……………...
6. Задания к лабораторной работе………………………………………………
7. Содержание отчета……………………………………………………………
8. Вопросы для самопроверки…………………………………………………..
Литература………………………………………………………………………..

 

 

Цель работы

 

Исследование статистических характеристик непреднамеренных радиопомех в диапазонах волн и определение на их основе параметров ЭМС радиоприемного устройства расположенного в изучаемой электромагнитной обстановке.

 

Краткие теоретические сведения

 

Радиоэлектронные средства (РЭС) благодаря своей эффективности используются практически во всех сферах человеческой деятельности, причем количество используемых РЭС наращивается быстрыми темпами. Одновременно работающие РЭС могут создавать помехи друг другу. Вероятность мешающего воздействия зависит от числа работающих РЭС и их тактико-технических характеристик (мощность излучения, чувствительность, избирательность и т.д.). Для увеличения плотности размещения одновременно работающих РЭС в пространственно-частотно-временном объеме необходимо тщательное изучение их мешающего взаимодействия.

В реальных условиях в точке расположения РЭС действует большое число различного рода излучений, учет которых возможен только при помощи методов теории вероятности и математической статистики. В дальнейшем мы будем рассматривать только те помехи от РЭС и других источников, которые не создаются специально и называются непреднамеренными радиопомехами (НРП).

Важнейшей характеристикой РПУ с точки зрения ЭМС является избирательность. Под избирательностью понимается способность РПУ выделять полезный сигнал из сложных электромагнитных полей, созданных в точке расположения РПУ. Для обеспечения избирательности используют отличия полезного сигнала от помех. Наиболее широко используются отличия по частоте, направлению прихода волны, поляризации, времени прихода сигналов и т.д.

 

 

Рис. 1. Модель радиоприемного устройства

 

Модель приёмника (рис.1) представляет собой последовательное включение линейных фильтров по различным параметрам: ФП – фильтр по пространству, ПФ – поляризационный фильтр, ЧФ₁ – частотный фильтр, характеристика избирательности, которого определяется частотной избирательностью антенны, входных цепей и усилителя высокой частоты, НЭ – нелинейный элемент, ЧФ₂ – частотный фильтр частотная характеристика, которого в основном определяется характеристикой ФОС, ВФ – временной фильтр, ФФ – фильтр по форме.

Под электромагнитной обстановкой (ЭМО) понимается совокупность излучений, образованных за счет совместной работы РЭС и других источников НРП в точке расположения приемного устройства рассматриваемой радиотехнической системы.

Можно отметить исключительное многообразие частотно-время-пространственных характеристик помех и многочисленность источников. Знание индивидуальных свойств каждого из них необходимо для оценки действия помех на радиосредства, расположенные в непосредственной близости от источника, и разработки эффективных мер защиты.

Для решения задач ЭМС необходимо составить модель ЭМО, позволяющую выявлять закономерности взаимного влияния совместно работающих РЭС.

Естественно, что модель – это лишь приблизительная копия, отражающая наиболее существенные особенности ЭМО. Для составления модели надо знать ряд факторов: относительное расположение источников мешающего излучения; энергетические характеристики мешающих сигналов; параметры помех определенные в интересующих нас диапазонах; число источников, создающих радиопомехи. Такая модель необходима для возможности количественно оценить ухудшение тактико-технических характеристик исследуемой РТС. Изобразим модель территориального расположения РЭС.

 

Рис. 2. Территориальная модель ЭМО

 

Территориальная модель ЭМО (рис.2) состоит из передатчика (РПдУ) и приемника (РПрУ), которые разнесены на расстояние D, близкое к максимальному для исследуемой РТС. Таким образом, приемное устройство принимает полезный сигнал на фоне N излучений от других РЭС, которые в данном случае являются мешающими. Приёмник должен выделить полезный сигнал из всей совокупности излучений. Основой для такого выделения служит отличие параметров сигнала от параметров помех.

Целесообразно все параметры сигналов разделить на энергетические и неэнергетические. К неэнергетическим параметрам относятся: несущая частота, направление прихода по азимуту и углу места, временные характеристики, поляризация. Энергетическими параметрами считают энергию сигнала, плотность потока мощности, напряженность поля, мощность, силу тока, напряжение и т.д.

Любой радиосигнал можно представить набором параметров х₁, х₂,..., х_n, каждый из которых принимает значения в соответствующих диапазонах D х ₁, D х ₂,..., D х _n. Таким образом, каждый сигнал можно представить в виде точки внутри некоторого n -мерного прямоугольного параллелепипеда со сторонами D х ₁, D х ₂,..., D х _n, координаты которой будут определяться параметрами х ₁, х ₂,..., х _n. Если в зоне досягаемости исследуемого приёмника действует N источников излучения, то внутри такого параллелепипеда будет N точек.

Координаты каждой точки будут случайны, а плотность заполнения неравномерна и описываться n -мерной плотностью распределения ω _n(х ₁, х ₂,..., х _n) параметров х ₁, х ₂,..., х _n.

Для большинства практических случаев параметры х ₁, х ₂,..., х _n независимы друг от друга, что объясняется двумя основными факторами:

– неэнергетические параметры независимы по своей физической природе и методу формирования;

– диапазоны изменения параметров считаются узкими, т.е. D x << x, а для независимых параметров n -мерную плотность распределения параметров можно представить как произведение одномерных плотностей по отдельным параметрам ω_n(х ₁, х ₂,..., х _n) = ω(х ₁) · ω(х ₂) ·....· ω(х _n).

 

Рис. 3. Распределение случайных точек в n -мерном параллелепипеде

 

В рассматриваемом n -мерном параллелепипеде (рис.3), общий объём которого

V = D х ₁ · D х ₂ ·... · D х _n = D х _i, (1)

 

можно выделить относительно малый объём DV' << V, охватывающий точку (х '₁, х '₂,..., х '_n), с ребрами, параллельными осям координат. По каждой из осей этот объём будет занимать отрезок DХ'_i, а сам объём

 

DV' = DХ'₁ · DХ'₂ ·...· DХ'_n = DХ_i (2)

 

можно представить как обобщенную полосу пропускания n -мерного фильтра состоящего из n фильтров по отдельным параметрам с полосой пропускания DХ_i. Будем считать, что все фильтры идеальные, т.е. имеют прямоугольную характеристику избирательности. Таким образом, в обобщённом объёме V, заполненным системой случайных точек с распределением ω_n(х₁, х₂,..., х_n), с помощью n -мерного фильтра выделена обобщённая полоса прозрачности.

Среднее число сигналов Nср попадающих в обобщенную полосу пропускания можно определить по формуле

Nср = NDV'ω_n(х '₁, х '₂,..., х '_n) = N DХ_i'ω(x '_i). (3)

 

Для обобщённой полосы пропускания можно применить распределение Пуассона:

(4)

 

где Vk – вероятность того, что событие А, вероятность появления которого равна р, в n опытах появиться ровно k раз, z = n × p.

В нашем случае под событием А подразумевается попадание помехи в обобщенную полосу прозрачности, тогда z – среднее число сигналов в объёме DV', т.е. z = Ncр.

Распишем данную формулу

 

V_k= exp(–NDV'ω_n(х '₁, х '₂,.... х '_n)) (NDV'ω_n(х '₁, х '₂,.... х '_n))^k =

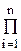= exp(–N DX'_iω(х '_i))(N 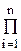DX'_iω(х '_i))^k. (5)

 

С помощью данного выражения можно найти ряд важных вероятностей:

– вероятность того, что в объёме DV' не будет ни одного излучения

V₀ = exp(–N 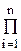DX'_iω(х '_i)); (6)

 

– вероятность того, что в объёме DV' будет только одно излучение

 

V₁ = exp(–N 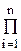DX'_iω(х '_i))(N 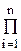DX'_iω(х '_i)); (7)

 

– вероятности того, что в объёме DV' будет не более одного излучения

 

V_{£ 1} = exp(–N 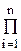DX'_iω(х '_i))(1+ N 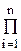DX'_iω(х '_i)) (8)

 

По смыслу V₀ характеризует ЭМС системы в целом и называется вероятностью ЭМС. Ее значение зависит от ЭМО, параметров РПУ и эффективности мешающего воздействия помех на полезный сигнал, а, следовательно, на возможность выполнения РТС своих функций.

Эта вероятность характеризует отсутствие помех на выходе приемника, в котором нет полезного сигнала и позволяет исключить из рассмотрения отношение сигнал/шум, что существенно упрощает методику исследования.

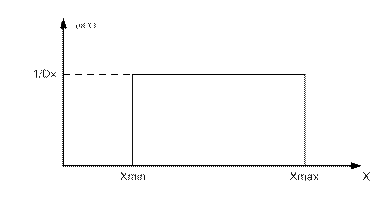
Рис. 4. Равномерный закон распределения

 

Как правило, распределение неэнергетических параметров внутри их диапазонов изменения можно описать равномерным законом ω_n(х) = 1/D x (рис.4), при этом формула для V₀ существенно упростится

 

V₀ = exp(–N 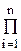DX'_i /D х _i), (9)

 

если селекция проводится только по одному параметру то

 

V₀ = exp(–NDX' /D х), (10)

 

Описание плотности распределения энергетических параметров нельзя свести только к равномерному закону, это может быть частным случаем, причем довольно редким. Ограничим рассмотрение этого вопроса ситуацией, когда помеха РПрУ наводится одним источником со случайным местоположением.

Для плотности потока мощности в точке приёма известно выражение

 

, (11)

 

где Р_изл – мощность излучения, G_изл – КНД излучающей антенны, у(j,e) – нормированная, снятая по мощности ДН передающей антенны.

Перепишем данную формулу в следующем виде: П = АР_э/R², где Р_э = = Р_излG_излу(j,e) – эквивалентная мощность излучения источника, А = 1/4p. Более кратко запишем П = xy, где х = АР_э, у = 1/R².

Для нахождения распределения ω(П) надо знать распределения ω(х) и ω(у). Рассмотрим два упрощенных случая.

Случай 1. Предположим, что все источники излучений имеют одинаковую эквивалентную мощность (Р_э = const) и распределены равномерно (рис.5) в плоском кольце, ограниченном радиусами Rmax и Rmin. Найдем для данного случая распределение ω(R). Площадь кольца dS = 2pR₁dR. Среднее число источников на этой площади DN = 2prR₁dR, где r – плотность источников излучения. Если весь интервал D_R = Rmax – Rmin разбить на равные части, число которых h = D_R/(dR), то плотность вероятностей найдем как предел ω(R) = (DN/(dR)) = bR, где b – нормирующий множитель.

Рис. 5. Равномерное по площади расположение источников помех

 

После нормировки получим

 

ω(R) = 2R/(R²max – R²min) (Rmin £ R £ Rmax).

 

Зная ω(R), нетрудно рассчитать ω(П) по формуле известной из теории вероятностей:

. (12)

 

Определив производную dП/dR = b₂/R² (b₁, b₂ постоянные коэффициенты) и проведя соответствующие подстановки и преобразования, получим:

 

(П_min £ П £ П_max) (13)

 

как правило П_max >> П_min, тогда

 

ω(П) = П_min/П² (П_min £ П £ П_max). (14)

 

Нас в основном будет интересовать распределение мощности

 

(Р_min £ Р £ Р_max). (15)

Случай 2. Предположим, что все источники излучения находятся на одинаковой дальности, тогда плотность распределения дальностей будет описываться дельта-функцией ω(R) = d(R_cp) (R_min £ R £ R_max). Таким образом ω(П) будет зависеть от распределения ω(Р_э). Эквивалентная мощность относится к величинам с большим динамическим диапазоном, для которых часто постулируют равномерно-логарифмическое распределение или распределение Шеннона:

 

(П_min £ П £ П_max). (16)

 

Для мощности сигнала запишем

 

(Р_min £ Р £ Р_max). (17)

 

В общем случае, применяя формулу П = ху, при известных ω(х) и ω(у) можно воспользоваться известным выражением

 

. (18)

 

Мы рассмотрели два случая распределения мощности сигналов ω(Р) в зависимости от распределения дальностей ω(R) и в обоих случаях получили, что распределение мощности описывается гиперболическим законом только с разными показателями степени. В общем, виде гиперболический закон распределения для мощностей записывается следующим образом:

 

ω(Р) = b/ (Р_min £ Р £ Р_max). (21)

 

где b - нормировочный коэффициент,

 

(22)

 

Нормировочный коэффициент b рассчитывается из условия нормировки

 

. (23)

 

Гиперболический закон является трехпараметрическим, его параметрами являются Р_max, P_min и степень m (рис. 6).

 

Понятно, что кроме гиперболического закона распределения могут применяться и другие. Все зависит от конкретной ситуации.

Энергетическую оценку ЭМС следует увязывать с отношением сигнал/помеха, от которого зависят большинство ТТХ системы. В реальных условиях на РПрУ воздействуют различного рода помехи, отличающиеся по своим временным, спектральным и другим характеристикам, влияние которых на РПрУ при одинаковых мощностях различно. Для устранения этого многообразия помех в исходных моделях ЭМО в [2] вводится понятие шумового эквивалента. Под шумовым эквивалентом непреднамеренной помехи понимается отношение реальной мощности данной помехи к мощности «белого» шума, попадающего в полосу РПдУ, при котором их влияние на тактико-технические характеристики РТС одинаково, то есть Р_р = hР_ш, Р_р – реальная мощность помехи, Р_ш – мощность шума, вызывающего такое же воздействие, как и непреднамеренная помеха, мощностью Р_р. Тогда шумовой эквивалент h = Р_р/Р_ш. Таким образом, под мощностью помехи мы подразумеваем не ее реальную мощность, а эквивалентную. Общую мощность помех на входе приемника можно определить как сумму:

 

Р_п = Р_ш + Р_м.с., (24)

 

где Р_ш – мощность собственных шумов, Р_м.с. – мощность мешающих сигналов.

Первое слагаемое в этой формуле является величиной детерминированной, т.е. в приемнике всегда имеются шумы уровень, которых практически не изменяется. Значение второго слагаемого величина случайная и может во много раз превышать уровень собственных шумов и приводить к частичной, либо полной потере работоспособности системы, однако, вероятность такого события, как правило, мала. Для нормальной работы приемника мощность полезного сигнала должна в какое-то число раз а превышать мощность собственных шумов Р_о = а Р_ш, а в условиях действия помех в а раз превышать суммарную мощность помех

 

P'_o = а (Р_ш + Р_м.с) = Р_о + а Р_м.с. (25)

 

Коэффициентом непреднамеренных помех называется число К_нп, которое показывает во сколько раз в среднем надо повысить порог приема в условиях воздействия непреднамеренных помех, чтобы сохранить превышение порогового уровня сигнала над помехой, таким же каким оно было до воздействия непреднамеренных помех. Исходя, из определения получаем

 

К_нп = P'_о/P_o = 1 + Р_м.с./Р_ш. (26)

 

С учетом электромагнитной обстановки и селективных свойств приемника, получим

 

(27)

 

Как видно из формулы коэффициент непреднамеренных помех определяется не только параметрами приемника, в данном случае мощность собственных шумов Р_ш и полосы пропускания по отдельным параметрам DX_i, а также параметрами ЭМО, средней мощностью помех Р_ср и плотностью распределения вероятности их неэнергетических параметров ω(x _i). Чем меньшее влияние оказывают помехи на работу РТС тем, меньше К_нп, поэтому меры по снижению К_нп являются мерами улучшения ЭМС.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: