 |
Определение плотности распределения и параметров случайных величин
|
|
|
|
Математическая статистика – раздел математики, посвященный установлению закономерностей случайных явлений или процессов на основании регистрации, систематизации и обработки результатов наблюдений или измерений [5].
Статистические методы исследования, базирующиеся на рассмотрении экспериментальных данных о тех или иных совокупностях объектов, применяются в самых различных областях знаний (физика, экономика, медицина и др.) и могут преследовать разные цели. Однако можно указать следующие три основные задачи математической статистики:
§ оценка неизвестной функции распределения или плотности вероятности. Эта задача обычно формулируется так. В результате независимых измерений случайной величины x получены следующие ее конкретные значения x = (x 1, х 2,..... х n). Требуется оценить неизвестную функцию распределения F (x) случайной величины x или ее плотность вероятности ω(x), если x - непрерывная случайная величина. Эту задачу можно распространить на многомерные функции распределения и плотности вероятности.
§ оценка неизвестных параметров закона распределения. Пусть на основании физических или общетеоретических соображений можно заключить, что случайная величина x имеет функцию распределения определенного вида, зависящую от нескольких параметров, значения которых неизвестны. На основании наблюдений величины x нужно оценить значения этих параметров.
§ статистическая проверка гипотез. Обычно эта задача формулируется следующим образом. Пусть на основании некоторых соображений можно считать, что функция распределения исследуемой случайной величины x есть F (x). Спрашивается, совместимы ли наблюденные значения с гипотезой, что случайная величина x действительно имеет распределение F (x).
|
|
|
Чтобы получить представление о распределении наблюдений, поступают следующим образом. На первом этапе производят многократное измерение случайной величины, получая простой статистический ряд (табл.1).
Таблица 1
| i - номер измерения | ....... | r | |||
| Результат измерения | x 1 | x 2 | x 3 | ....... | xr |
Однако статистический материал в виде простого статистического ряда при большом числе измерений трудно обозрим, по нему практически невозможно оценить закон распределения исследуемого параметра x.
Поэтому для визуальной оценки закона распределения исследуемой случайной величины x производят группировку данных.
Область экспериментальных значений случайной величины разбивают на r обычно одинаковых интервалов длины D x и вычисляют частость попадания случайной величины х в i -тый интервал. В результате получаем сгруппированный статистический ряд следующего вида (табл. 2).
Таблица 2
| Dxi интервал | D x 1 | D x 2 | D x 3 | ....... | D x r |
частость 
| 
| 
| 
| ....... | 
|
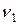
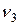
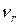
Частость в данном случае характеризует вероятность попадания случайной величины х в i -тый интервал.
Используя данные табл. 2 можно определить все числовые характеристики случайной величины наиболее важными, из которых являются математическое ожидание (средне статистическое значение) и дисперсия.
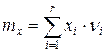, (28)
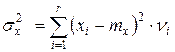, (29)
где x i значение случайной величины соответствующее средине i -того интервала.
Относительная плотность точек в каждом интервале определяется как отношение частости попадания в этот интервал n к его длине Dx (табл.3):
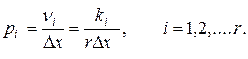(30)
где ki – число экспериментальных точек в i -м интервале, ni = ki/r.
Таблица 3.
| Dxi интервал | D x 1 | D x 2 | D x 3 | ....... | D xr |
плотность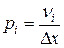 
| 
| 
| 
| ....... | 
|
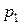
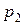
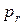
Подсчитанные таким образом значения можно представить графически в виде ступенчатой кривой: по оси абсцисс откладывают соответствующие интервалы и на каждом из них, на основании, строится прямоугольник, высота которого равна относительной плотности pi. Полученная ступенчатая кривая называется гистограммой. Гистограмма частостей статистического ряда представлена на рис. 7.
|
|
|
Рис.7. Гистограмма частостей статического ряда
Гистограмма дает наглядное представление о распределении наблюденных значений на числовой оси. По ней можно определить частоту попадания наблюденных значений в любой интервал числовой оси. Очевидно, что все величины pi неотрицательны, причем суммарная площадь под гистограммой равна единице:
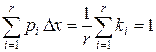. (31)
При заданном числе наблюдений r гистограмма, составленная на основе группировки с достаточно малыми интервалами, обычно многовершинная и не отражает наглядно существенных свойств распределения. С другой стороны, группировка по слишком крупным интервалам может привести к потере ясного представления о характере распределения и к грубым ошибкам при вычислении других характеристик распределения.
Для выбора оптимальной длины интервалов, т.е. такой длины частичных интервалов, при которой статистический ряд не будет очень громоздким и в нем не исчезнут особенности исследуемой случайной величины, рекомендуют формулу
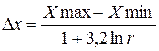, (32)
где r – объем выборки, D x – длина интервала.
Количество интервалов выбирается, как правило, обычно не меньше 5 и не больше 15.
Аналогично строиться гистограмма в двумерном случае, когда рассматривается распределение данных на плоскости (например, при анализе рассеивания при стрельбе или бомбометании). Разбив часть плоскости, занятую экспериментальными точками, на прямоугольники и подсчитав число точек в каждом прямоугольнике, можно определить соответствующие относительные плотности точек как отношение частоты попадания в прямоугольник к его площади.
Во многих случаях возникает необходимость аппроксимации экспериментально полученной гистограммы подходящим аналитическим выражением, представляющим собой некоторый теоретический закон распределения или плотность вероятности, которые должны удовлетворять двум обязательным условиям: неотрицательности и нормировки. Эта операция называется выравниванием статистических данных. При этом естественно стремятся к тому, чтобы такая аппроксимация (выравнивание) в определенном смысле была наилучшей.
|
|
|
Имеется много разнообразных способов и приемов подбора распределений для экспериментальных данных и невозможно выделить какой-либо из них. Успех в значительной степени определяется накопившемся опытом в этом деле. Однако можно дать некоторые общие рекомендации.
Обычно аппроксимация гистограммы является не самоцелью, а производится для получения каких-либо выводов о физическом механизме изучаемого явления или процесса или же для выполнения последующих расчетов. Исходя из этого, прежде всего, необходимо принять решение - аппроксимировать ли гистограмму дискретным или непрерывным распределением (плотностью вероятности). После этого производится качественное сопоставление характера построенной гистограммы с графиком различных теоретических распределений (дискретных или непрерывных) и по близости их поведения останавливаются на каком-либо одном из наиболее подходящих.
В зависимости от решаемой задачи характер и степень близости поведения следует понимать по-разному: иногда можно ограничиться хорошим совпадением в центральной области (области больших вероятностей), а иногда (например, в теории обнаружения сигналов) нужно стремиться к хорошему совпадению на «крыльях» закона распределения (в области малых вероятностей).
|
|
|
