Формирователь модулирующих сигналов

Формирователь модулирующих сигналов (ФМС) предназначен для преобразования двоичного цифрового потока от кодера C (t) в модулирующие сигналы I (t) и Q (t), которые необходимо подавать на синфазный и квадратурный входы модулятора для получения заданного сигнального созвездия на его выходе. Он должен содержать:

- регистр сдвига для деления входного потока бит от кодера на группы, передаваемые одним сигналом s _КАМ(t) (дибиты при QPSK);

- преобразователи уровней битовых сигналов (униполярной кодировки в биполярную: при QPSK «0» → h, «1» → – h; при QASK «00» → 3 h, «01» → h, «10» → – h, «11» → –3 h);

 

Требуется:

1. Изобразить сигнальное созвездие для заданного вида модуляции.

 

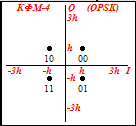
Рис. 3.4.1. Сигнальное созвездия четырехуровневой QPSK

 

2. Изобразить график реализации c (t) случайного процесса C (t)

на входе блока ФМС (выходе сверточного кодера) для первых 16 бинарных интервалов (рис. 3.4.2).

С(t)

h

1 1 1 Т_б

L ih2+Rdzlu+8E//l5l7cAAAD//wMAUEsDBBQABgAIAAAAIQBEh/xb2wAAAAkBAAAPAAAAZHJzL2Rv d25yZXYueG1sTI/NTsMwEITvSLyDtUjcqFMjAg1xKoSExJGmHDg68TY/xGvLdpv07XHFAY47O5r5 ptwuZmIn9GGwJGG9yoAhtVYP1En43L/dPQELUZFWkyWUcMYA2+r6qlSFtjPt8FTHjqUQCoWS0Mfo Cs5D26NRYWUdUvodrDcqptN3XHs1p3AzcZFlOTdqoNTQK4evPbbf9dFI+PLNKN7PsxN2zOvN6FB8 7FDK25vl5RlYxCX+meGCn9ChSkyNPZIObJIgHkTaEiXkjwJYMtyvL0LzK/Cq5P8XVD8AAAD//wMA UEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEAoGoj3fYBAAAEBAAADgAAAAAAAAAAAAAAAAAuAgAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEARIf8W9sAAAAJAQAADwAAAAAAAAAAAAAAAABQBAAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAFgFAAAAAA== " strokecolor="#4f81bd [3204]" strokeweight="2pt">

-h 0

 

Рис. 3.4.2. Осциллограмма реализации 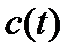с выхода сверточного кодера

 

Написать аналитическое выражение для случайного процесса .

где ­ прямоугольный импульс длительностью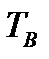

при

где ­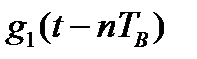 прямоугольный импульс такой же формы, как , но сдвинутый вправо относительно импульса на величину , если , или влево, если 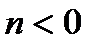; 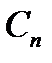- случайная величина 0, + h (значение бита на - интервале ).

 

3. В соответствии с сигнальным созвездием модулятора QPSK

(или QASK) изобразить для входной реализации графики реализаций и на выходе блока ФМС случайных процессов и (рис. 3.4.3). Написать аналитические выражения для случайных процессов и .

;

где ­ прямоугольный импульс длительностью T_S.

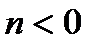­ прямоугольный импульс такой же формы, как импульс , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; и ­ независимые случайные величины, заданные на символьном интервале с номером 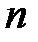, которые согласно сигнальному созвездию (рис. 3.4.1) принимают:

для QPSK два дискретных значения – h, + h с вероятностью 0,5 каждое, т. е. ;

 

С(t)

h

1 1 1 Т_б

/ Iq7yz+8E//F3198BAAD//wMAUEsDBBQABgAIAAAAIQBEh/xb2wAAAAkBAAAPAAAAZHJzL2Rvd25y ZXYueG1sTI/NTsMwEITvSLyDtUjcqFMjAg1xKoSExJGmHDg68TY/xGvLdpv07XHFAY47O5r5ptwu ZmIn9GGwJGG9yoAhtVYP1En43L/dPQELUZFWkyWUcMYA2+r6qlSFtjPt8FTHjqUQCoWS0MfoCs5D 26NRYWUdUvodrDcqptN3XHs1p3AzcZFlOTdqoNTQK4evPbbf9dFI+PLNKN7PsxN2zOvN6FB87FDK 25vl5RlYxCX+meGCn9ChSkyNPZIObJIgHkTaEiXkjwJYMtyvL0LzK/Cq5P8XVD8AAAD//wMAUEsB Ai0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAzqzgYPMBAAADBAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uy b0RvYy54bWxQSwECLQAUAAYACAAAACEARIf8W9sAAAAJAQAADwAAAAAAAAAAAAAAAABNBAAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAFUFAAAAAA== " strokecolor="#4f81bd [3204]" strokeweight="2pt">

-h 0

I(t)

 

 

 

 

 

 

Q(t)

 

 

 

 

Рис.

 

3.4.3. Осциллограммы реализаций i (t) q (t) на выходах и ФМС

 

4. Написать аналитические выражения для корреляционной функции

и спектральной плотности мощности входного случайного процесса и построить графики этих функций.

Процесс C (t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид [1]

,при

0,при

а энергетический спектр

,

где Т = Т_В – длительность тактового интервала.

Графики B _C(τ) и G_C (f) приведены на рис. 3.4.4.

 

Рис. 3.4.4. Корреляционная функция B _C(τ) (а) и энергетический спектр G_C (f) (б)

синхронного телеграфного сигнала C (t)

 

5. Написать аналитические выражения для корреляционных функций

B_I (τ) и B_Q (τ), спектральных плотностей мощности G_I (f) и G_Q (f) случайных процессов I (t) и Q (t). Построить графики этих функций.

Процессы I (t) и Q (t) отличаются от процесса C (t) длительностями тактовых интервалов (T_S = 2 T_B для QPSK и T_S = 4 T_B для QАSK), а для QАSK ещё и начальными значениями B_I (0) = B_Q (0) = D [ I (t)] = D [ Q (t)] и G_I (0) = G_Q (0) = D [ I (t)]/ T_S = D [ Q (t)]/ T_S

корреляционная функция имеет вид [1]

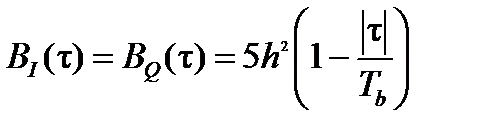,при

0,при

а энергетический спектр

,

Графики B _I(τ) и G_I (f) приведены на рис. 3.4.5.

Рис. 3.4.5. Корреляционная функция B _I(τ) (а) и энергетический G_I (f) спектр (б) синхронного телеграфного сигнала I (t)

6. Определить длительность символьного интервала T_S.

T_S = 2 T_B для QPSK,

где T_B - бинарный интервал.

T_S = 2 T_B = 2·1,8 = 3,6 мкс

 

Модулятор

В состав модулятора входят блоки:

- генератор несущего колебания U cosω_С t,

- фазовращатель на – для получения квадратурного несущего колебания U sinω_С t,

- перемножители ПМ 1 и ПМ 2, для получения БМ сигналов S_I (t) = I (t)cosω_С t и S_Q (t) = Q (t)sinω_С t, модулированных сигналами I (t) и Q (t), соответственно;

- сумматор для получения сигнала с квадратурной модуляцией

S _КАМ(t) = S_I (t) + S_Q (t) = I (t)cosω_С t + Q (t)sinω_С t.

Х

Y

Х

Г

-900

Х

∑

Вход В(t) А

 

Выход

 

 

Б

 

Рис.3.5. Схема модулятора КФМ-4.

Формулу для определения сигнального созвездия можно представить в следующем виде:

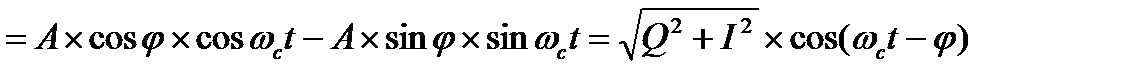
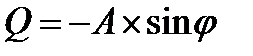; – фазу отсчитывают по круговому направлению против часовой стрелки, так как в выражении для Q перед А стоит знак минус. Таким образом, при считывании фазы с сигнального созвездия меняем знак по мнимой оси на противоположный (см. знак «минус» перед А в выражении для Q)

1. На четырех символьных интервалах T_S нарисовать графики следующих сигналов (в виде символических прямоугольников с указанием их амплитуд и фаз, определенных по сигнальному созвездию заданного вида модуляции):

синфазного БМ сигнала ;

квадратурного БМ сигнала ;

сигнала заданной квадратурной модуляции ;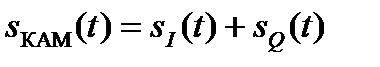

кодовой последовательности с выхода кодера (без учета их временных сдвигов для удобства сопоставления).

 

 

С(t)

h

1 1 1 Т_б

-h 0

I(t)

 

 

 

 

Q(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 3.5.1. Построения графиков

для сигналов КФМ-4 в блоке модулятора

 

 

 

1 t

 

-1

 

Рис.3.5.2.Сигнал заданной квадратурной модуляции на выходе сумматора в квазигармонической форме.

 

2. Написать аналитические выражения для корреляционных функций B_SI (τ), B_SQ (τ) и для спектральных плотностей мощности G_SI (f) и G_SQ (f) сигналов S_I (t) и S_Q (t) на выходах перемножителей модулятора.

Из анализа, приведенного в [2, стр. 41 – 42], следует

,

 

 

аналогично

Спектральные плотности мощности G_SI (f) и G_SQ (f) сигналов S_I (t) и S_Q (t) можно найти по теореме Винера-Хинчина как преобразование Фурье от их корреляционных функций [2, стр.43]

,

.

3. Написать аналитические выражения для корреляционной функции сигнала B_S (τ) и для спектральной плотности мощности G_S (f) сигнала S _КАМ(t) заданного вида квадратурной модуляции на выходесумматора модулятора. Построить графики этих функций.

Учитывая, что процесс S _КАМ(t) является суммой двух случайных независимых процессов S_I (t) и S_Q (t)

S _КАМ(t) = S_I (t) + S_Q (t) = I (t)cosω_С t + Q (t)sinω_С t,

его корреляционная функция будет равна сумме корреляционных функций слагаемых процессов

B_S (τ) = B_SI (τ) + B_SQ (τ) =

По этой же причине спектральная плотность мощности G_S (f) сигнала S _КАМ(t) есть сумма энергетических спектров G_SI (f) и G_SQ (f) сигналов S_I (t) и S_Q (t), соответственно,

.

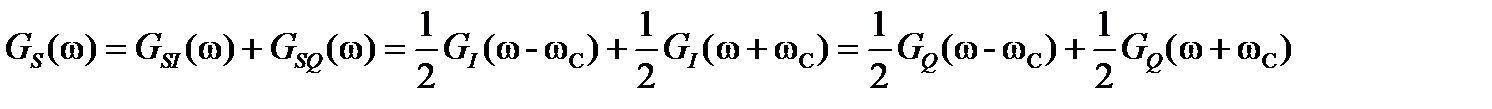Графики B_S (τ) и G_S (f) приведены на рис. 3.5.3.

 

τ

ω

cos

)

(

)

τ

(

c

×

=

t

I

S

B

B

S

T

S

T

-

τ

τ

ω

cos

)

(

)

τ

(

c

cos

×

=

t

I

I

B

B

 

Рис. 3.5.3. График корреляционной функции случайного процесса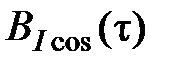

Рис. 3.5.3 График функции

4. Определить F_S – ширину спектра модулированного сигнала S _КАМ(t) по второму нулю его огибающей

1438 кГц

Непрерывный канал

Передача сигнала s _КАМ(t) происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии

аддитивной помехи типа гауссовского белого шума (АБГШ). Сигнал на выходе такого канала имеет вид

z (t) = μ s _КАМ(t) + n (t),

где μ – коэффициент передачи канала. Для всех вариантов принять μ = 1. Односторонняя спектральная плотность мощности помехи равна N _О

(значения N _О для своего варианта взять из таблицы исходных данных).

 

Требуется:

1. Определить минимально необходимую ширину полосы частот непрерывного канала F _К.

=1,44 МГц;

2. Определить мощность помехи на выходе канала.

Р _П = N _O· F_k = 1,85·10^-7·144·10³ = 0,26 В²

3. Определить ­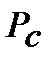 среднюю мощность сигнала s (t) и найти отношение / .

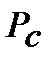4. Рассчитать пропускную способность 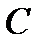(за секунду) непрерывного канала.

 

5. Оценить эффективность использования пропускной способности непрерывного канала, равную отношению производительности источника к пропускной способности канала, т. е.

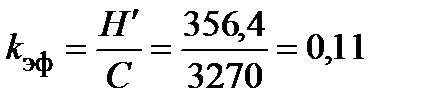
где

 

Демодулятор

 

Когерентный демодулятор производит анализ принятого приёмником смеси переданного сигнала с помехой z (t) = μ s _КАМ(t) + n (t), сопоставляя его с известными образцами сигналов, формируемых модулятором. Анализ завершается принятием решения по критерию максимального правдоподобия в пользу наиболее вероятного передаваемого сигнала (символа).

Требуется:

1. Изобразить структурную схему когерентного демодулятора,

оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции (рис. 3.7.1).

 

Рис. 3.7.1. Схема демодулятора для сигнала квадратурной модуляции КФМ-4

 

 

2. Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора.

.

В момент окончания каждого символьного интервала длительностью решающее устройство РУ1 (и РУ2) определяет номер входа , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате:

«00» при = 1, «10» при = 2, «01» при = 3, «11» при = 4.

3. Определить вероятности ошибок на выходах решающих устройств РУ1 и РУ2 при определении значений символов I_n и Q_n, равных h, –h

,

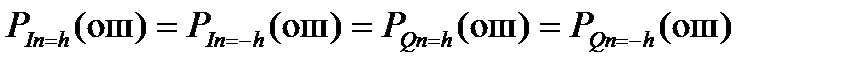где P_{In = x} (ош) и P_{Qn = x} (ош)­ – вероятности ошибочного приема при In = x и Qn = x, соответственно,

Передаваемые величины In и Qn	Вероятность ошибки в работе РУ1 и РУ2
In = ± h, Qn = ± h	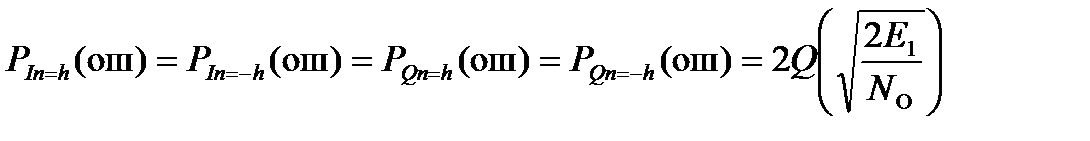, где Q (x)– дополнительная функция ошибок, Е 1 - энергия сигнала 1·cosωc t, Е 1 = 0,5·12· TS N O – спектральная плотность мощности БГШ

=

 

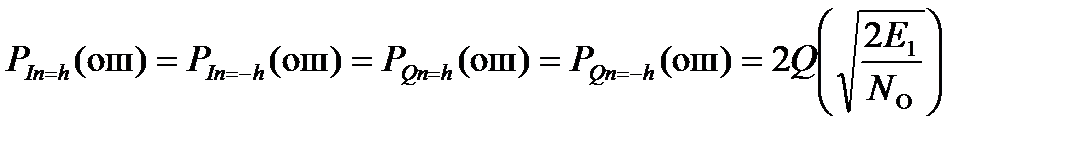4. Определить вероятности ошибок на выходе преобразователя

параллельного кода в последовательный код (ФМС) для заданных параметров сигналов и :

для точек сигнального созвездия с координатами I_n = ± h, Q_n = ± h (4 точки у QPSK)

P _In=h,Qn=h(ош) = P_In=h (ош) + P_Qn=h (ош) – P_In=h (ош)· P_Qn=h (ош)= ,

 

5. Определить среднюю вероятность ошибки на выходе преобразователя:

для QPSK:

P _ср(ош) = 4· P _In=h,Qn=h(ош) / 4 = P _In=h,Qn=h(ош)= .

Декодер

Декодер формирует из непрерывной последовательности кодовых символов, поступающих с выхода демодулятора (возможно, с ошибками), выходную непрерывную последовательность декодированных кодовых символов, в которых ошибки частично либо полностью исправлены.

 

Требуется:

1. Переписать последовательность кодовых символов, полученных на выходе кодера из п. 4 раздела 3.3

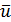= 001101011111011001.

 

2. Получить входную для декодера последовательность кодовых символов путём внесения в последовательность однократной ошибки в позиции q (по варианту)

=000^x101011111011001 (при q = 3).

 

3. Построить решетчатые диаграммы выживших путей декодера для моментов: t ₁ – t ₄, t ₁ – t ₅, t ₁ – t ₆, t ₁ – t ₇, t ₁ – t ₈, t ₁ – t ₉, t ₁ – t ₁₀, t ₁ – t ₄ (рис. 3.8.1). На построенных диаграммах, вычислить метрики путей, входящих в каждый узел диаграммы, выделить фрагменты единственно выживших путей и прочитать по ним декодированную кодовую последовательность â _ВЫХ(k). Убедиться в том, что â _ВЫХ(k) = b _ВЫХ(k), т.е. в исправлении ошибки в позиции q.

Рис. 3.8.1. Решетчатая диаграмма декодера (степень кодирования ½,К=3)

Решетчатая диаграмма декодера на рис 3.8.1. отличается от решетчатой диаграммы кодера на рис 3.3.1 тем, что ребрам этих решеток соответствуют разные обозначения. Числа над ребрами решетки декодера определяются, как расстояние Хемминга между двумя символами принятой последовательности , расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера.

 

1.Тепер построим честь решетчатой диаграммы декодера, которая расположена между моментами t₁ и t₄. Для удобства узлы обозначим буквами

a,b,c,d и a,y,l,n.

Определим метрику путей по Хеммингу, исходящих из одной точки a и приходящих в узлы d,k,m,p.

Из диаграммы видно, что в узел d приходят два пути a,b,c,d и a,y,l,d. Определим по диаграмме метрику этих путей

Г_a,b,c,d=0+1+1= 2

Г_a,y,l,d=2+2+1=5

В узел k приходят так же два пути a,b,c,k и a,y,l,d. Их метрики равны

Г_a,b,c,k=0+1+1=2

Г_a,y,l,k=2+2+1=5

 

В узел m приходят так же два пути a,b,z,m и a,y,n,m. Их метрики равны

Г_a,b,z,m=0+1+2=3

Г_a,y,n,m=2+0+0=2

В узел p приходят так же два пути a,b,z,p и a,y,n,p. Их метрики равны

Г_a,b,z,p=0+1+0=1

Г_a,y,n,p=2+0+2=4.

Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов d,k,m,p, выжившим считается только один путь-тот путь, которому соответствует меньшая метрика. С учетом этого, из двух путей, приходящих в узел a, выживает узел a,b,c,d. Из остальных пар выживут соответственно a,b,c,k; a,y,n,m; a,b,z,p.

Снова построим диаграмму, но на ней укажем только выжившие пути к моменту времени t₄ (Рис. 3.8.1, a.). Теперь полученную диаграмму на рис (Рис. 3.8.1, б.) достроим соответствующими ребрами до момента t₅(из каждого узла d,k,m,p проводим два новых ребра).

 

 

 

 

Рис. 3.8.1, a. Решетчатая диаграмма декодера Рис. 3.8.1, б. Выжившие пути к моменту времени t_4.

между моментами t₁ и t_4.

 

2. Выжившие пути к моменту времени t₄, достроенные до момента t₅.

В узел j приходят два пути a,b,c,d,j и a,y,n,m,j; метрика этих путей равна:

Г_a,b,c,d,j= 0+1+1+1=3

Г_a,y,n,m,j=2+0+0+1=3

В узел f приходят также два пути a,b,c,d,f и a,y,n,m,f:

Г_a,b,c,d,f=3

Г_a,y,n,m,f=3

В узел v приходят также два пути a,b,c,k,v и a,b,z,p,v:

Г_a,b,c,k,v=4

Г_a,b,z,p,v=1

В узел q приходят также два пути a,b,c,k,q и a,b,z,p,q:

Г_a,b,c,k,q=2

Г_a,b,z,p,q=3

 

Двум путям, приходящих в узел j, соответствую одинаковые расстояние Хемминга, равные 3. Поэтому из этих двух путей произвольно выбираем любой, например, a,b,c,d,j. Аналогично из двух путей, приходящий в узел f, произвольно выбираем любой путь, например, a,b,c,d,f. Из двух путей, приходящих в узел v: a,b,z,p,v. Из двух путей приходящих в узел q: a,b,c,k,q.

 

Рис.3.8.1.в. Выжившие пути к моменту t_4, достроенные до момента t₅.

 

3.Выжившие пути к моменту t₅, достроенные до моменты t₆.

Узел i: Г_a,b,c,d,j,i=5

Г_a,b,z,p,v,i=1

Узел o: Г_a,b,c,d,j,o=3

Г_a,b,z,p,v,o=3

Узел w: Г_a,b,c,d,f,w=4

Г_a,b,c,k,q,w=3

Узел e: Г_a,b,c,d,f,e=4

Г_a,b,c,k,q,e=3

Рис.3.8.1.г. Выжившие пути к моменту t_5,достроенные до момента t₆ .

 

Согласно вышесказанному выживают следующие пути: a,b,z,p,v,i; a,b,z,p,v,o; a,b,c,k,q,w; a,b,c,k,q,e. На диаграмме (рис. 3.8.1.г.) строим эти пути.

 

4. Выжившие пути к моменту t₆, достроенные до момента t_7.

Узел y: Г_{a,b,c,k,q,w,y}=3

Г_{a,b,z,p,v,I,y}=3

Узел m: Г_{a,b,c,k,q,w,m}=5

Г_{a,b,z,p,v,i,m}=1

Узел ф: Г_{a,b,c,k,q,e,ф}=4

Г_{a,b,z,p,v,o,ф}=4

Узел и: Г_{a,b,c,k,q,e,u}=4

Г_{a,b,z,p,v,o,u}=4

 

 

Рис.3.8.1.д. Выжившие пути к моменту t₆ , достроенные до момента t₇.

 

Выживают пути a,b,z,p,v,i,y; a,b,z,p,v,I,m; a,b,z,p,v,o,ф; a,b,z,p,v,o,u.

 

5. Выжившие пути к моменту t_7, достроенные до момента t₈

Достраиваем полученную диаграмму соответствующими ребрами до момента t₈ и указываем над вновь проведенными ребрами на рис.3.8.1.е. соответствующие расстояние Хемминга.

Находим:

Узел я: Г_{a,b,z,p,v,I,y,я}=4

Г_{a,b,z,p,v,o,ф,я}=5

Узел э: Г_{a,b,z,p,v,I,y,э}=4

Г_{a,b,z,p,v,o,ф,э}=5

Узел ю: Г_{a,b,z,p,v,I,m,ю}=3

Г_{a,b,z,p,v,o,u,ю}=4

Узел ь: Г_{a,b,z,p,v,I,m,ь}=1

Г_{a,b,z,p,v,o,u,ь}=6

 

 

Рис.3.8.1.е. Выжившие пути к моменту t₇ , достроенные до момента t₈.

 

Выживают пути a,b,z,p,v,I,y,я; a,b,z,p,v,I,y,э; a,b,z,p,v,I,m,ю; a,b,z,p,v,I,m,ь.

 

6. Выжившие пути к моменту t_8, достроенные до момента t₉ и т.д. вычерчивают сигнал на диаграмме кодера. Изобразим диаграмму от момента t₁₁ до момента t₁₂.

 

 

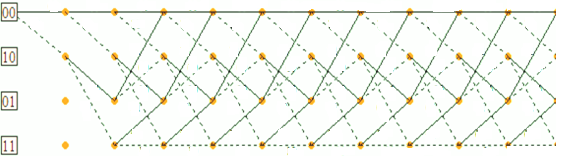
Рис.3.8.1.ж. Выжившие пути к моменту t₁₁ , достроенные до момента t₁₂.

 

7. Из построенной на рис 3.8.1.ж. диаграммы видно,что от момента t₁ до момента t₁₀ выжил только один путь a,b,z,p,v,I,m,ь,г,ш,м. Теперь перенесем этот один выживший путь с диаграммы декодера на диаграмму кодера. Этому пути на диаграмме кодера соответствуют обозначения ребер 00, 11, 01, 01,11,11,01,10,01.

 

Рис.3.8.1.з. Выживший путь к моменту t₁₀ на диаграмме декодера.

Декодер принимает решение, что на интервале от t₁ до t₁₀ по каналу передавалась последовательность кодовых символов, соответствующая выжившему пути a,b,z,p,v,I,m,ь,г,ш,м, т.е.: 00, 11, 01, 01,11,11,01,10,01. Эта последовательность совпадает с 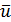= 001101011111011001 от момента t₁ до t₁₀ . Таким образом, ошибки возникшие на выходе демодулятора, оказываются исправленными.

 

ЛИТЕРАТУРА

1. Сальников А.П. Теория электрической связи: Конспект лекций / СПбГУТ. – СПб., 2007. – 273 с.: ил.

2. Общая теория связи: методические указания к выполнению курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб.: Издательство СПбГУТ, 2012. – 80 с.

3.. Теория электрической связи:учеб.пособие для студ.высших учебных заведений / Р.Р. Биккенин, М.Н. Чесноков. - СПб.:Издательский центр «Академия», 2010.-336с.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: