Способ и средства управления

 

 

18.1.1. Назначение автоматического управления. Гребные электрические установки состоят из нескольких частей и в этом смысле являются сложными системами. Для облегчения управления и сокращения обслуживающего персонала вводится комплексная автоматизация ГЭУ, охватывающая тепло-производящую установку, тепловой двигатель, генератор, распределительные и преобразовательные устройства и системы управления всех перечисленных частей.

Тепловой двигатель и электрическая передача (генератор и гребной электродвигатель) снабжаются системами автоматического регулирования (САР). У теплового двигателя регулируется частота вращения, а в системе генератор — двигатель — ток главной цепи, момент вращения или мощность.

В дальнейшем рассматриваются только САР, относящиеся к электрической части ГЭУ, т. е. генератору и ГЭД со всеми промежуточными устройствами, системами возбуждения и управления.

К САР ГЭУ предъявляются различные требования в зависимости от назначения судна, уровня технической оснащенности и обслуживания. Назначение САР состоит в том, чтобы получать наибольшую эффективность действия ГЭУ, т. е. иметь наилучшие показатели качества по всем или главным управляемым величинам координат. Такое управление является оптимальным.

Точность поддержания заданных значений регулируемых координат зависит от совершенства измерительных устройств; нижний предел погрешности регулирования устанавливается 1—2%. Погрешность регулирования в процентах е равна ста процентам минус точность регулирования заданной координаты в процентах.

18.1.2. Критерии оптимального управления. Эксплуатация является оптимальной, когда перевозится наибольшее количество груза с наименьшими затратами и в заданные сроки, достигается наибольшая скорость судна, наибольшее усилие при движении во льдах или при ходе с возом.

ГЭУ действуют в условиях переменного момента сопротивления (наличие качки судна или движение во льдах). В этом случае управление можно считать оптимальным, если имеет место мини­мум расхода энергии (топлива) и сохранение срока службы тепловых двигателей.

В работе решается задача определения оптимального управления судном, движущимся при нерегулярном волнении с минимальным расходом энергии на расстояние S за время Т. Заданные условия удовлетворяются при постоянной частоте вращения гребного винта (n = const). Для уменьшения максимальных моментов на гребном винте снижают частоту вращения гребного винта, а следовательно, и скорость судна. Такой способ управления является оптимальным для судов с непосредственным или редукторным соединением теплового двигателя с гребным валом и судов с ГЭУ переменного тока по системе СГ — СД или АД.

Для судов с ГЭУ постоянного тока, выполненных по системам СГ — В—Д, Г — Д или вентильных, во время качки возможно использование тепловых двигателей при неизменных частоте и моменте вращения, что улучшает условия работы двигателей и увеличивает срок их службы, главным образом дизелей. Это позволяет увеличить скорость судна, так как изменения момента сопротивления на гребном винте воспринимаются только электродвигателем.

Система автоматического управления изменяет магнитный по­ток генератора обратно пропорционально току главной цепи, изменяющемуся пропорционально моменту сопротивления на гребном винте, вследствие чего момент сопротивления генератора поддерживается постоянным, и тепловой двигатель работает с постоянной частотой вращения.

Тот же результат можно получить, если изменять магнитный поток ГЭД обратно пропорционально его частоте вращения, вследствие чего противо-ЭДС электродвигателя остается, постоянной, а вместе с ней остается неизменным ток главной цепи и момент сопротивления генератора, так как его магнитный поток не регулируется. ГЭД действует с переменными частотой и моментом вращения.

В работе также рассмотрена задача определения оптимального закона управления для судна, движущегося с переменным сопротивлением (ход во льдах) на заданном участке пути в определенное время. Решение приводит к получению постоянного расхода энергии или иначе — постоянной мощности СЭУ. В этом случае автоматическая система управления ГЭУ ледокола и буксира должна поддерживать постоянство мощности, воздействуя на маг­нитный поток ГЭД.

Системы управления должны также иметь требуемое качество переходного процесса. Наиболее частыми переходными процессами являются пуски, реверсы, остановки и изменения скорости судна. Время изменения режима движения судна измеряется минутами, а время электромеханического переходного процесса ГЭД — несколькими секундами, вследствие чего продолжительность переходного процесса не влияет существенно на время изменения скорости судна при разгоне или торможении.

Большое значение имеют переходные процессы при ограничениях токов, напряжений, моментов и частоты вращения во время возникновения перегрузок на гребном винте и при восстановлении прежнего режима. Поэтому необходимо так оптимизировать переходный процесс в ГЭУ, чтобы было возможно наиболее быстрое приведение величин к заданным значениям при допустимом перерегулировании.

18.1.3. Выбор управляющих устройств (регуляторов). Метод последовательной коррекции. В теории и практике проектирования электропривода пользуются методом последовательной коррекции, который дает возможность сразу получить устойчивую систему с требуемым качеством переходного процесса.

Последовательное включение корректирующих звеньев, которые являются и управляющими органами, стало возможным благодаря применению электронных усилителей и вентильных (тиристорных) преобразователей. Для управления тиристорными преобразователями, являющимися мощными усилителями, требуются сигналы малой мощности, что позволяет применять операционные усилители и интегральные схемы с различными суммирующими, интегрирующими и другими блоками. Нашей промышленностью разработаны и выпускаются универсальные блоки системы регулирования (УБСР) на интегральных схемах для управления вентильными преобразователями. Эти блоки могут использоваться и для управления другими элементами, например машинными усилителями в сочетании с промежуточными электронными или вентильными усилителями.

Метод последовательной коррекции и подчиненного управления достаточно подробно описан в литературе. Однако этот метод не нашел широкого применения в ГЭУ. Здесь дается его краткое изложение и приводится выбор управляющих устройств автоматической системы.

Система управления является оптимальной по качеству переходного процесса в случае стремления к минимуму функционала

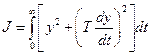, (18.1)

где Т = const — постоянная времени; у(t) — отклонение управляемой величины, или ошибка. Экстремалью данного функционала, т. е. кривой, дающей минимальное значение интеграла (18.1), является экспонента 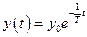при начальном значении у = у₀. Если у₀ = 1, то J_min = Т, что получается прямым интегрированием. В общем случае J_min = J* вычисляется для каждого типа системы и соответствует требуемой кривой переходного процесса.

Функционал (18.1) представляет интегральный критерий качества переходного процесса и позволяет найти связь между параметрами системы и параметрами переходного процесса без построения кривой у(t).

Для систем промышленного электропривода считается оптимальным процесс, имеющий максимальное перерегулирование σ_тах управляемой величины не выше 5%, ограниченное время регули­рования t_peг и ошибку, укладывающуюся в требуемые пределы.

В ГЭУ могут быть приняты эти же значения перерегулирования и ошибка, не превышающая 2% (ε ≤ 2%).

График процесса, соответствующего так называемому «техническому оптимуму», показан на рис. 18.1. Такой график может быть получен в системе управления, переходные процессы которой описываются уравнением второго порядка

(T₁²p² + T₂p + l)y(t) = k(t),

и после приведения к относительному времени τ = t / Т₁ имеет

характеристическое уравнение вида

р² + Ар + 1=0,

где А = Т₂ / Т₁, р = d/dt.

Решением уравнения является экспонента, как и экстремаль функционала (5.1), которая может дать оптимальный переходный процесс. Это имеет место, когда А =√2, при τ = 1.

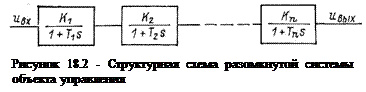В ГЭУ при возмущающих воздействиях отклонение тока может значительно превосходить номинальный, и переходный процесс уже носит иной характер, чем при управляющем воздействии, но точность управления не нарушается. С целью получения оптимального переходного процесса необходимо систему линейных дифференциальных уравнений, описывающих переходный процесс автоматической системы и преобразованных по Лапласу, привести к уравнению второго порядка, для чего используются последовательно включаемые регуляторы, одновременно являющиеся и корректирующими звеньями.

Метод последовательной коррекции основан на алгебраических преобразованиях передаточных функций автоматических систем. В простейшем случае математическая модель объекта управления состоит из цепи апериодических звеньев направленного действия, что характерно для электропривода (рис. 18.2), и описывается системой дифференциальных уравнений первой степени.

Передаточная функция разомкнутой цепи равна

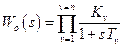. (18.2)

Для компенсации инерционных звеньев системы управления необходимо последовательно с объектом включить управляющее устройство (регулятор) с передаточной функцией

W_y(s) = K_y 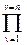(1+sT_v), (18.3)

в результате чего передаточная функция разомкнутой скорректированной системы управления преобразуется к виду

W_раз.ск(s) = K_y K₁ K₂ К_п, (18.4)

а замкнутой системы с коэффициентом обратной связи К_о.с:

W_замк_ (s) = 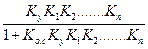. (18.5)

Приведенная полная компенсация не только невозможна, но и вредна, так как выходная величина должна мгновенно изменяться вместе с входной, для чего потребуется большое быстродействие и форсировочная способность регулирующих органов, в том числе возбудителей генераторов и ГЭД ГЭУ, а следовательно, увеличение их мощности. Система окажется чувствительной ко всем внутренним и внешним факторам, будет не защищенной от помех.

Практически найдено, что можно компенсировать апериодические звенья с большой постоянной времени, не увеличивая мощность соответствующих органов, и оставлять нескомпенсирован-ными малые постоянные времени. Кроме того, для повышения точности и снижения астатизма применяют интегрирующие звенья при ограниченном коэффициенте усиления.

В результате передаточная функция разомкнутой скорректированной системы должна иметь вид

W_раз.ск(s)= W_о(s) W_у(s)= 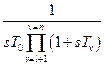. (18.6)

Компенсация больших постоянных времени действует только при малых отклонениях. При больших отклонениях управляющей или возмущающей величины происходит запаздывание, вызванное ограничением мощности и форсировки регулирующих органов. Оставшиеся нескомпенсированными п — l звеньев имеют малые постоянные времени, и без особой погрешности можно пренебречь их произведением, оставив только сумму:

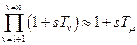, (18.7)

где

.

Исследования показывают, что если Т₀ >2 Т_μ, то погрешность весьма незначительна.

Если замкнутая система с К = 1 и К_о.с. = 1 имеет характеристическое уравнение

sT₀ (l+sТ_μ)+l=0,

то при Т₀ = 2 Т_μ перерегулирование не превосходит 5%, а при Т₀ =4 Т_μ процесс будет апериодическим.

Коэффициент усиления разомкнутой скомпенсированной системы на основании выражений (18.4) и (18.6) должен быть равен

К_раз = 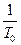= K_y K₁ K₂ К_п К_о.с.,

откуда

К_у = 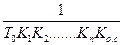. (18.8)

 

Здесь Т₀ и Ко. с. малы, поэтому Ку может быть достаточно большим.

Для получения (18.6) управляющее устройство должно иметь следующую передаточную функцию:

W_y(s) = 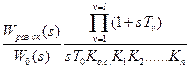. (18.9)

Разомкнутая скомпенсированная система показана на рис. 18.3. Для получения структурной схемы с единичной обратной связью Ко.с. введено в Ку (18.8). В этом случае передаточная функция замкнутой системы принимает вид

W_замк(s) = 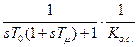. (18.10)

Как показали исследования, в системе с передаточной функцией (18.10) минимальная длительность переходного процесса обеспечивается в случае Т₀ = 2 Т_μ, при этом перерегулирование составляет около 5%. Когда Т₀ > 2 Т_μ, перерегулирование уменьшается, и когда Т₀ = 4 Т_μ, процесс становится апериодическим. Следовательно, процесс будет оптимальным при условии 2 Т_μ < Т₀ <4 Т_μ.

Метод подчиненного управления. Гребная электрическая установка имеет несколько переменных, подлежащих управлению: это — ток электродвигателя, частота вращения, мощность или момент вращения. Система управления является многоконтурной, с перекрещивающимися связями.

Изложенные выше способ выбора управляющего устройства и условия оптимизации справедливы и для многоконтурных систем ГЭУ.

Многоконтурные системы с последовательным включением управляющих устройств (рис.18.4) получили название систем подчиненного управления. Для таких систем разработан следующий способ синтеза. На рис. 6.4 W₀₁, W₀₂,..., W_on — передаточные функции объектов управления; W_y1, W_y2,..., W_yn — передаточные функции управляющих устройств; y₁, у₂,..., у_n — управляемые переменные величины. Входной сигнал у_вх проходит через все n управляющих устройств и n объектов управления и задает

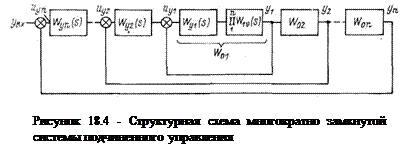
выходную величину у_n. Промежуточные управляющие устройства накладывают ограничения на все управляемые величины y₁, у₂,..., у_n-1 в соответствии с заданными законами управления. Такая система применяется в случае взаимосвязанных управляемых величин, как это имеет место в ГЭУ.

Передаточная функция первого объекта управления W₀₁ состоит из компенсируемой W_о.к1 и некомпенсируемой W_о.н1, частей: W₀₁ = W_о.к1W_о.н1. После компенсации с принятой оптимизацией передаточная функция первого замкнутого контура W_з1 имеет вид (18.10). Множитель 1/К_о.с входит в Wy1.

Передаточная функция для управляемой величины у₂ состоит из произведения передаточных функций внутреннего замкнутого контура W_з1 (s) и второго объекта управления:

W_02раз(s) = 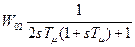. (18.11)

В знаменателе этого выражения пренебрегают членом второго порядка, принимая

2sТ_μ(1+sТ_μ) + 1=2s²Т²_μ+2sТ_μ + 1 ≈2sТ_μ +1. (18.12)

В общем случае

W_0vраз(s) = . (18.13)

Передаточная функция v- й управляемой величины включает в себя в качестве нескомпенсированной части линейное приближение передаточной функции замкнутого (v — 1)-го контура.

По условию оптимальности Т₀ = 2 Т_μ. В этом случае Т_μv = 2 ^v-1 Т_μ1 и передаточная функция v -го управляющего устройства равна:

W_yv(s) = 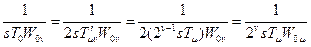. (18.14)

Передаточная функция v -гo замкнутого контура при К_{о. с} = 1 имеет вид

W_замк(s)= 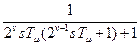. (18.15)

Системы повышенного быстродействия. В ГЭУ автоматическая система должна реагировать на управляющие и возмущающие воздействия, при этом она должна обладать достаточно большим быстродействием при изменениях нагрузки (возмущениях), особенно для ледоколов и ГЭУ неизменного тока. Системы, настроенные по техническому оптимуму, могут иметь недостаточное быстродействие. В этих случаях применяются АС с большим быстродействием с управляющими устройствами, включаемыми в каждый контур управления.

ГЭУ состоит из направленных апериодических звеньев. Путем разделения контуров по методу подчиненного управления структурная схема ГЭУ приводится к системе с последовательным соединением звеньев, что позволяет легко найти в общем виде переда­точную функцию регулятора, приводящего реальную передаточную функцию к третьему порядку с желаемой ЛАЧХ.

Такое построение системы управления и приведение передаточной функции к желаемой сделано для систем электропривода. Метод получил название симметричного оптимума. В этом случае регулятор, включаемый последовательно на вход системы управления и компенсирующий два апериодических звена с постоянными времени Т₁ и Т₂, должен иметь передаточную функцию вида

W_y(s) = 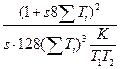, (18.16)

где ∑ Т_i,- — сумма некомпенсируемых малых постоянных времени исходной системы; К — коэффициент усиления объекта управления.

Передаточные функции разомкнутой и замкнутой систем управления будут:

W_раз (s)= 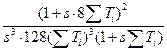; (18.17)

W_замк(s) = 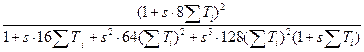. (5.18)

Изложенные выше способы последовательной коррекции сов­падают с частотным методом построения желаемой ЛАЧХ и ЛФЧХ.

В ГЭУ регуляторы, как правило, действуют одновременно только в режимах, определяемых точками излома механической характеристики ГЭД. Обычно регуляторы действуют раздельно. Поэтому и выбирать их следует независимо друг от друга, что упрощает как отыскание передаточной функции регулятора, так и настройку системы.

18.2.1. Уравнения ГЭУ и их линеаризация. Системы автоматического управления широко используются в ГЭУ постоянного тока на судах с тяжелыми или меняющимися условиями плавания. В дальнейшем рассматриваются системы автоматического управления в применении к ГЭУ постоянного тока, т. е. системы СГ — В - Д и Г - Д.

Для синтеза систем управления используются уравнения для расчета переходных процессов. Эти уравнения подвергаются линеаризации известными методами с заменой производных приращениями переменных величин.

После линеаризации система уравнений ГЭУ постоянного тока принимает следующий вид:

уравнение движения ГЭД

Ф_д.k*Δi_* + i_k*ΔФ_д* = n²_k*Δk _в* +2k _{вk *} n_k*Δn_* + Т_мр Δn_*, (18.19)

где

Т_м= 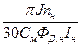, р= ,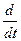

уравнение якорной цепи

Δе_г* = К₁Δi_*(1 + Т_ар) + К₂Ф_дk*Δn_* + К₂n_k*ΔФ_д*, (18.20)

уравнение цепи возбуждения генератора

Δи_в*= (1+ Т_вр) Δе_г*, (18.21)

уравнение возбудителя генератора

К_{Т. в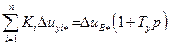} , (18.22)

уравнение цепи возбуждения ГЭД

Δи_вд*= (1+ Т_др)ΔФ_д*, (18.23)

уравнение возбудителя ГЭД

К_т.в.д 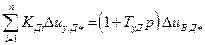, (18.24)

где ,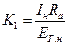

,

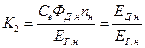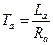уравнение звена сравнения и регулятора тока

(Δи _з.т* - К_ТΔi_*) W_y.T(p) = Δи_у.Т*. (18.25)

уравнение звена сравнения и регулятора мощности генератора, действующего на возбуждение генератора,

(Δи_з.Р* -K_Pi_k* Δе_r*- K_P е_Гk* Δi_*)W_yP(p)= Δи_у.P*, (18.26)

уравнение звена сравнения и регулятора напряжения генератора

(Δи _{з. u*} - К_uΔи_*) W_y.u(p) = Δи_у.u*, (18.27)

уравнение звена сравнения и регулятора частоты вращения ГЭД

(Δи_з.n* - К_n*Δn_*) W_y.n(p) = Δи_у.n*, (18.28)

уравнение звена сравнения и регулятора мощности ГЭД, действующего на возбуждение ГЭД

(Δи_з.Д* -K_Д*i_k* Δе_Г*- K_Д*е_Гk* Δi_*)W_yД(p)= Δи_у.Д*. (18.29)

В последних уравнениях W_y.T, W_yP, W_yu, W_yn, W_y.д — соответственно передаточные функции регуляторов тока, мощности генератора, напряжения, частоты вращения ГЭД и мощности ГЭД.

Если линеаризация произведена в точке номинального режима, то все постоянные значения переменных на данном участке отклонения от номинального режима в о.е., обозначенные индексом «k», равны единице:

Ф_Дk = ф_Д.н; i_k = I_н; n_k = n_н; k_Bk = k_B.н,

Ф_Дk*= i_k*= n_k*= k_Bk*=1.

После такой замены, принимая Δх = х, уравнения (18.19) — (18.29) приведем к следующему упрощенному виду:

i +Ф_Д=k_B+2n+ T_Mpn, (18.30)

е_Г = K₁i (1 + Т_ар)+К₂п + К₂Ф_Д, (18.31)

и_В.Г = (1+Т _В.Г р)е_Г, (18.32)

К_{Т. в} , (18.33)

и_вД=(1+ Т_Др)Ф_Д, (18.34)

К_{Т.в . Д} , (18.35)

(и_з.Т - i)W_y.Т(p) = и_y.Т, (18.36)

(и_з.Р - е_Г- i)W_y.Р(p) = и_y.Р, (18.37)

(и_з.u - u_Г) W_y 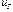(p) = и_у 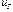, (18.38)

(и_з.n - n)W_yn(p) = и_уn, (18.39)

(и_з.Д – i-е_Г)W_yД(p)=и_у.Д. . (18.40)

18.2.2. Функциональные схемы управления. Предпосылки к выбору схемы. Выбор схемы управления зависит от назначения гребной электрической установки и, следовательно, от предъявляемых к ней требований. Требуемые механические характеристики ГЭД и внешние характеристики генератора могут быть получены разными средствами. Оптималь­ная в эксплуатационном отношении установка в режимах переменного сопротивления движению судна может поддерживать постоян­ство мощности тепловых двигателей в широких пределах изменением тока и напряжения генератора или в ограниченных пределах (от швартовной характеристики до хода в свободной воде) измене­нием магнитного потока ГЭД. Аналогичным образом регулирова­ние частоты вращения ГЭД можно осуществлять изменением напряжения генератора или ослаблением магнитного потока ГЭД, так как магнитный поток ГЭД не может быть больше номинального значения, соответствующего наиболее тяжелому режиму.

Вопросы для самоконтроля.

1. Назначение автоматического управления.
2. Критерии оптимального управления.
3. Выбор управляющих устройств (регуляторов).
4. Уравнения ГЭУ и их линеаризация.
5. Функциональные схемы управления.

 

 

Список использованной литературы

 

 

1. Богомолов В.С. Гребные электрические установки: теория и эксплуатация. – Калининград: Калининградское книжное издательство, 1998. - 223 с.

2. Хайкин А.Б., Васильев В.Н., Полонский В.И. Автоматизированные гребные электрические установки. – М.: Транспорт, 1986. - 424 с.

3. Рукавишников С.Б. Автоматизированные гребные электрические установки. – Л.: Судостроение, 1983. - 240 с.

4. Теория судового электропривода: учебное пособие / К.А.Чекунов. – Л.: Судостроение, 1982. - 336 с.

5. Правила классификации и постройки морских судов. Регистр. - Л.: Транспорт, 1995.

6. Гребные электрические установки: cправочник / Е.Б. Айзенштадт, Ю.М. Гилерович, Б.А. Горбунов, Сержантов В.В. – 2-е изд., перераб. и доп. – Л.: Судостроение, 1985. – 304 с.

 

 

Ó Титов Владимир Владимирович

 

⇐ Предыдущая6789101112131415

Поделиться:

Воспользуйтесь поиском по сайту: