 |
Векторная величина в средней школе.
|
|
|
|
Большое место в школьном курсе физике занимают векторные величины. Понятие векторной величины тесно связано с понятием вектора, но не тождественно ему. Векторная величина характеризует какое-либо свойство тела, явления, процесса, существующие реально; её можно измерить. Понятия «измерение вектора» не существует.
Физика оперирует векторными величинами, которые задаются указанием размера и направления в пространстве. Поэтому направленный отрезок является удобным наглядным изображением векторной величины. Операцию построения направленного отрезка MN, для которого  равен
равен  , можно назвать откладыванием какой-либо векторной величины
, можно назвать откладыванием какой-либо векторной величины  от точки М [7].
от точки М [7].
При определении многих физических величин (а также при записях некоторых законов) подчеркивается и векторный характер, в то время как расчет численных значений этих величин выполняется в скалярной форме. В связи с этим возникает необходимость разъяснения учащимся основных приемов и правил перехода от уравнений, записанных в векторной форме, к уравнениям в скалярной форме.
Первые затруднения возникают при записи уравнения кинематики прямолинейного равнопеременного движения. В этом случае [9] для решения основной задачи механики достаточно оперировать двумя уравнениями: уравнением для мгновенной скорости

и уравнением для координаты
 ,
,
где х0 – координата начальной точки, V0x и ax – проекции векторов  на ось Х, которая параллельна траектории движения.
на ось Х, которая параллельна траектории движения.
Для решения многих задач достаточно знать только численное значение мгновенной скорости, определяемое из соответствующего уравнения в скалярной форме. Для этого нужно уравнения мгновенной скорости записать для её проекции на ось х, т.е.
|
|
|
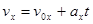 .
.
Таким образом, основная задача механики решается с помощью двух независимых уравнений:

 .
.
Если начало координат совпадает с начальной точкой движения уравнения упрощаются и принимают вид:

 .
.
Кроме уравнения координаты вводится также формула для вычисления пути (путь – скалярная величина, равная длине траектории):
 .
.
Четкое представление о величинах, входящих в уравнения мгновенной скорости и координаты, и об их изменениях с течением времени складывается у учащихся при вычерчивании графиков.
На рисунке 2.4 показано изменения проекций векторов  , а также координаты х тела, брошенного вертикально вверх.
, а также координаты х тела, брошенного вертикально вверх.
Рис 2.4 и 2.5
На рисунке 2.5 изображены графики изменения ускорения и скорости тела по модулю, а также график его пути [7].
Уравнения динамики первоначально также даются в векторной форме. И естественно возникает необходимость перехода к записи их в скалярной форме.
Второй закон Ньютона учащиеся выражают следующим образом [14]:  , где
, где  - равнодействующая всех сил, приложенных к телу. В некоторых учебных пособиях это же уравнение записывается так:
- равнодействующая всех сил, приложенных к телу. В некоторых учебных пособиях это же уравнение записывается так:
 .
.
Для перехода к скалярной форме записи можно рекомендовать следующий прем. Допустим, что к телу приложены две силы  и
и  . Тогда телу сообщается ускорение
. Тогда телу сообщается ускорение  , направленное в сторону равнодействующей (рис.2.6):
, направленное в сторону равнодействующей (рис.2.6):
Рис 2.6.
Если спроецировать вектора  и
и  на произвольную ось х, то, учитывая пропорциональность отрезков, отсеченных на сторонах угла параллельными прямыми, можно записать:
на произвольную ось х, то, учитывая пропорциональность отрезков, отсеченных на сторонах угла параллельными прямыми, можно записать:
 .
.
Откуда  , где
, где  - проекция равнодействующей на ось х.
- проекция равнодействующей на ось х.
Из рисунка 2.6 также видно, что проекция равнодействующей равно сумме проекций приложенных сил, то есть
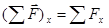 ,
,
следовательно,  .
.
Последнее уравнение выражает очень важное следствие: сумма проекций сил, приложенных к телу, по любой оси равна произведению массы тела на проекцию ускорения по этой же оси.
В практике средней школы встречаются физические задачи, которые сводятся к нахождению решений системы уравнений, из которых одни есть уравнения динамики, а другие – кинематики. Если в задаче рассматривается равноускоренное движение, то её решение не зависит от того, проекции или модули векторов входят в уравнения кинематики. Если же в задаче рассматривается равнозамедленное движение, то необходимо предварительно выразить все уравнения системы через однородные величины, то есть через модули соответствующих векторов. В этом случае формула скорости  имеет вид
имеет вид  , формула пути
, формула пути  будет, а формула
будет, а формула  выразится так
выразится так  .
.
|
|
|
Несоблюдение этого правила часто приводит к ошибочным решениям. Рассмотрим это на примере следующей задачи (задача №4 из упр. 17 учебника для 9 класса):
«Конькобежец, масса которого равна 50 кг, после разгона скользит по льду, пройдя до остановки 40 м. Сила трения постоянна и равна 10 Н. Сколько времени продолжается торможение?»
рис 2.7
Выполнив чертеж, обращаем внимание учащихся на то, что к конькобежцу приложены три силы: сила тяжести  , сила реакции
, сила реакции  (направленная нормально поверхности движения конькобежца) и сила сопротивления
(направленная нормально поверхности движения конькобежца) и сила сопротивления  . Рассмотрим проекции этих сил на вертикальную ось y и запишем соответствующее уравнение динамики:
. Рассмотрим проекции этих сил на вертикальную ось y и запишем соответствующее уравнение динамики:
 , так как
, так как 
поскольку  , то
, то  .
.
Между тем для проекций на ось х уравнение динамики имеет вид:

откуда (поскольку  и
и  ) получим:
) получим:
 , или
, или 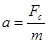 (где
(где  и
и  - модули векторов
- модули векторов  и
и  ).
).
Искомую величину - время – можно определить из уравнений кинематики:

Если теперь выразить проекции векторов через их модули, то получим:

Откуда находим, что  , или
, или  . Поскольку
. Поскольку  , то
, то  .
.
Обычно учащиеся поступают по другому: они записывают уравнения согласно учебнику так:

Откуда получают  или
или  . Если заранее не сделать разъяснений, то ученики считают, что величины, входящие в формулы, - модули соответствующих векторов и тогда знак минус вызывает у них недоумение. Если же произвести дальнейшее преобразования и подставить в последнюю формулу
. Если заранее не сделать разъяснений, то ученики считают, что величины, входящие в формулы, - модули соответствующих векторов и тогда знак минус вызывает у них недоумение. Если же произвести дальнейшее преобразования и подставить в последнюю формулу  , то получиться
, то получиться 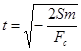 .
.
Этот результат вызывает у школьников ещё большее неумение, так как им не ясно, как избавиться от знака минус.
В данной задаче легко найти выход из затруднительного положения. Однако в более сложных задачах можно не заметить этого и получить неправильный ответ.
|
|
|
Поэтому имеет смысл на первом этапе решения по динамике рассматривать только случаи равноускоренного движения тел, а затем, после приобретения учащимися прочных знаний навыков, осторожно перейти к анализу и решению задач на равнозамедленное движение.
|
|
|


