 |
Решение.. Энергия магнитного поля катушки пропорциональна её индуктивности и квадрату силы тока:
|
|
|
|
Решение.
Общий вид зависимости напряжения на конденсаторе в колебательном контуре:  где
где  — амплитудное значение напряжения. Сравнивая с
— амплитудное значение напряжения. Сравнивая с  находим, что
находим, что 
 Значение максимального заряда на обкладках конденсатора равно
Значение максимального заряда на обкладках конденсатора равно  Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением
Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением  Отсюда находим
Отсюда находим 
Ответ: 0, 12
Задание 7. 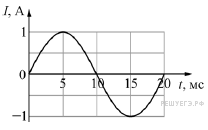 Электрический ток протекает через катушку индуктивностью 6 мГн. На графике приведена зависимость силы I этого тока от времени t. Чему равна энергия магнитного поля (в мДж), запасённая в катушке в момент времени t = 15 мс?
Электрический ток протекает через катушку индуктивностью 6 мГн. На графике приведена зависимость силы I этого тока от времени t. Чему равна энергия магнитного поля (в мДж), запасённая в катушке в момент времени t = 15 мс?
Решение.
Энергия магнитного поля катушки пропорциональна её индуктивности и квадрату силы тока: 
В момент времени  сила тока равна –1 А. Энергия равна
сила тока равна –1 А. Энергия равна

Ответ: 3 мДж
Задание 8. В колебательном контуре, состоящем из конденсатора и катушки индуктивности, происходят свободные электромагнитные колебания. В момент, когда конденсатор разряжен, параллельно к нему подключают второй такой же конденсатор. Как после этого изменятся следующие физические величины: запасенная в контуре энергия, частота свободных электромагнитных колебаний, амплитуда напряжения между пластинами первого конденсатора?
Для каждой величины определите соотвествующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
|
|
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | |||||||
А) Запасенная в контуре энергия
Б) Частота свободных электромагнитных колебаний
В) Амплитуда напряжения между пластинами первого конденсатора | 1) Увеличится 2) Уменьшится 3) Не изменится |
Решение.
При параллельном подключении к конденсатору еще одного такого же конденсатора общая емкость колебательного контура удваивается (при параллельном соединении емкости складываются). Поскольку в момент подключения первый конденсатора разряжен, никаких мгновенных перераспределений заряда на конденсаторах не происходит. Просто, начиная с этого момента, они начинают вместе заряжаться/разряжаться. Так как они подключены параллельно, в любой момент времени напряжения на них совпадают. Обсудим, как изменяются необходимые нам физические величины в результате такого изменения контура.
Частота свободных колебаний связана с емкостью контура соотношением 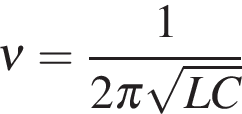 . Следовательно, увеличение емкости контура приводит к уменьшению частоты (Б — 2).
. Следовательно, увеличение емкости контура приводит к уменьшению частоты (Б — 2).
В момент подключения второго конденсатора вся энергия запасена в катушке индуктивности. Следовательно, как уже отмечалось в самом начале, подключение конденсатора не приводит к перезарядке конденсаторов, так как нечему перезаряжаться. А потому, изменение емкости контура не приводит к изменению запасенной в контуре энергии (А — 3).
Напряжения на конденсаторах совпадает. Энергия электрического поля, запасенная в конденсаторе, связана с напряжением на нем соотношением  Поскольку энергия колебаний не изменяется, максимальное значение энергии электрического поля в контуре сохраняется. Следовательно, увеличением емкости контура приводит к уменьшению напряжения на первом конденсаторе (В — 2):
Поскольку энергия колебаний не изменяется, максимальное значение энергии электрического поля в контуре сохраняется. Следовательно, увеличением емкости контура приводит к уменьшению напряжения на первом конденсаторе (В — 2): 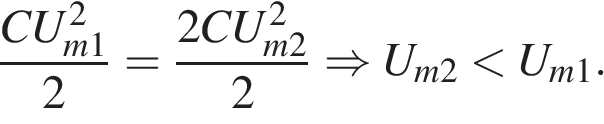
|
|
|
Ответ: 322
Задание 9 Идеальный колебательный контур состоит из конденсатора ёмкостью 0, 2  , заряженного до напряжения 10
, заряженного до напряжения 10 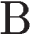 , катушки индуктивностью 2
, катушки индуктивностью 2  и разомкнутого ключа. После замыкания ключа, которое произошло в момент времени
и разомкнутого ключа. После замыкания ключа, которое произошло в момент времени  , в контуре возникли собственные электромагнитные колебания. Установите соответствие между зависимостями, полученными при исследовании этих колебаний (см. левый столбец), и формулами, выражающими эти зависимости (см. правый столбец; коэффициенты в формулах выражены в соответствующих единицах СИ без кратных и дольных множителей).
, в контуре возникли собственные электромагнитные колебания. Установите соответствие между зависимостями, полученными при исследовании этих колебаний (см. левый столбец), и формулами, выражающими эти зависимости (см. правый столбец; коэффициенты в формулах выражены в соответствующих единицах СИ без кратных и дольных множителей).
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ЗАВИСИМОСТЬ | ФОРМУЛА | |||||
А) Зависимость напряжения на конденсаторе от времени
Б) Зависимость силы тока, текущего через катушку, от времени | 1)  2)
2) 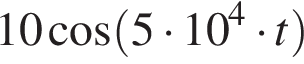 3)
3)  4)
4) 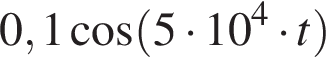
|
Решение. Рассчитаем сперва циклическую частоту собственных колебаний в контуре: 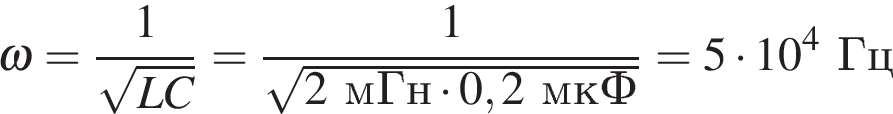 .
.
В начальный момент времени заряд конденсатора и напряжение на нем максимальны, отсюда можно найти амплитуду заряда:  .
.
Поскольку изначально конденсатора заряжен, для зависимости величины заряда на обкладке конденсатора можем написать:  . Таким образом, зависимость силы тока в контуре от времени дается выражением:
. Таким образом, зависимость силы тока в контуре от времени дается выражением:  . Следовательно, зависимость силы тока от времени дается формулой 3.
. Следовательно, зависимость силы тока от времени дается формулой 3.
Зависимость напряжения на конденсаторе от времени:  , то есть искомый закон дается формулой 2.
, то есть искомый закон дается формулой 2.
Правильный ответ: 23
|
|
|
Примечание: общий знак всех величин не имеет особого значения, так как под зарядом конденсатора мы можем понимать заряд любой из обкладок, а они противоположны. Аналогично с напряжением, разность потенциалов можно мерить между первой и второй, а можно наоборот. Важно уловить общий вид зависимости (амплитуду и фазу)
Ответ: 23
Задание 10. Проволочное кольцо находится в однородном магнитном поле, линии индукции которого перпендикулярны плоскости кольца. Модуль индукции магнитного поля уменьшают с постоянной скоростью. Затем кольцо заменяют на другое, вдвое большей площади, сохраняя прежнее расположение кольца относительно линий индукции. При этом скорость изменения модуля индукции магнитного поля уменьшают в 4 раза. Как в результате этого изменятся следующие физические величины:
А) магнитный поток через контур кольца в момент начала изменения модуля магнитной индукции и Б) ЭДС индукции, возникающая в кольце.
Для каждой величины определите соответствующий характер изменения:
1) увеличится 2) уменьшится 3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Магнитный поток через контур кольца в момент начала изменения модуля магнитной индукции | ЭДС индукции, возникающая в кольце |
|
|
|


