 |
Решение. Сила Ампера действует только на сторону рамки, параллельную границе магнитного поля, при этом она равна
|
|
|
|
Решение.
Согласно закону Фарадея, при изменении магнитного потока через замкнутый контур, в нем возникает ЭДС индукции величиной 
Для магнитного поля, перпендикулярного плоскости рамки, магнитный поток определяется как произведение величины индукции магнитного поля на площадь части рамки, пронизываемой полем: 
. Поле не изменяется по величине, поэтому изменение потока определяется только за счет изменения площади 
. При этом пока рамка пересекает границы магнитного поля площадь изменяется на величину 
за время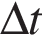 
. Следовательно, в рамке возникает ЭДС величиной 
. Величину индукционного тока можно найти из закона Ома: 
Сила Ампера действует только на сторону рамки, параллельную границе магнитного поля, при этом она равна
. Таким образом, искомая величина индукции магнитного поля:
Ответ: 0, 1 Тл.
Задание 18. Прямолинейный проводник длиной 80 см и массой 200 г, по которому течёт постоянный ток силой 0, 5 А, находится в однородном магнитном поле с индукцией 2 Тл. Проводник уравновешен в горизонтальном положении на опоре (см. рисунок) с помощью непроводящей нити. Чему равен модуль силы натяжения нити? Ответ приведите в Н.
Решение.
Сила Ампера, действующая на проводник с током в магнитном поле рассчитывается по формуле 
где 
— длина проводника. Направление силы Ампера определяется правилом левой руки, которое гласит, что если ладонь левой руки расположить так, чтобы вытянутые пальцы были направлены по току, а силовые линии магнитного поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник. В данном случае сила Ампера направлена вниз.
|
|
|
Рассмотрим моменты сил относительно оси, проходящей через точку опоры. На проводник действует сила тяжести и сила Ампера, направленные вниз и приложенные к центру проводника, сила реакции опоры, действующая вверх и проходящая через точку опоры, и сила натяжения нити, действующая вверх, приложенная к левому концу проводника. Чтобы тело находилось в покое, необходимо, чтобы сумма моментов сил, действующих на тело была равна нулю:
Ответ: 1, 4 Н.
Задание 19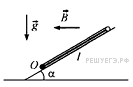 
Квадратная проводящая рамка со стороной l = 50 см и массой m = 400 г лежит на наклонной плоскости с углом наклона к горизонту, равным 
Нижняя горизонтальная сторона рамки шарнирно прикреплена к плоскости так, что рамка может без трения поворачиваться вокруг оси О, проходящей через эту сторону (см. рис., вид сбоку). Система находится в однородном горизонтальном магнитном поле с индукцией В = 1 Тл, направленной перпендикулярно оси О. Ток какой силой I и в каком направлении надо пропускать по рамке, чтобы она начала приподниматься над плоскостью, поворачиваясь вокруг оси O?
Решение.
Рамка с током начнёт поворачиваться, когда момент сил относительно оси O, действующий на рамку в магнитном поле, превысит момент силы тяжести. Если пропускать ток через рамку, то на все стороны рамки будет действовать сила Ампера. Моменты силы, приложенные к боковым сторонам, лежащим в плоскости рисунка будут уравновешивать друг друга, создавая противоположно направленные и равные по модулю моменты сил. Сила FA, действующая на верхнюю горизонтальную сторону рамки, по модулю равна BIl и должна действовать вверх, для чего ток в ней должен идти «от нас», за плоскость рисунка (см. рис. ). Плечо этой силы относительно оси O равно lcos α , а момент силы равен BIl2cosα .
|
|
|
Момент силы тяжести относительно оси O равен 
Таким образом, должно выполнятся соотношение
откуда 
|
|
|
