Моделирование погрешностей выходных параметров РЭУ

(прогнозирование разброса результатов испытаний)

На этапе проектирования и подготовки производства возникают задачи установления связи между допусками на параметры элементов РЭУ и выходными параметрами РЭУ в целом.

При анализе параметров РЭУ можно выделить два подхода.

В первом методе производится расчетрасчёт или подбор опытным путемпутём номинальных значений первичных параметров. Выбирают такие, которые обеспечивают требуемые значения выходных параметров. При этом не учитывают возможности отклонения фактически получаемых параметров от их номинальных значений в результате наличия множества производственных погрешностей и технологического разброса параметров элементов.

 

Во втором методе, обычно на втором этапе, анализируют влияние технологических погрешностей параметров элементов на значения выходных параметров. На параметры элементов назначают такие производственные допуски, которые еще обеспечивают требуемое качество функционирования РЭУ. Одна из задач, которые возникают на этом этапе, состоит в следующем.

Пусть известна математическая модель, которая связывает j-й выходной параметр с параметрами элементов х₁,...,х_п:

y_j = j(x₁,¼x_n); j=1,¼,m

где т — число принятых во внимание выходных параметров, характеризующих функционирование РЭУ. При этом работа РЭУ рассматривается статически в фиксированный момент времени и при определенныхопределённых значениях входных сигналов.

В качестве исходных данных должны быть известны вероятностные характеристики отклонений фактического значения x_i от его номинального уровня (D x_i = x_i - x_{i ном}). Указанные характеристики могут быть получены экспериментально, путемпутём контроля больших партий элементов, или на основании теоретических заключений, по документации на элементы. В результате решения нужно найти вероятностные характеристики выходных параметров РЭУ. Одной из таких характеристик является вероятность попадания выходного параметра y в заданный диапазон от y _j.mim до y _j.max. Эта вероятность определяет процент выхода годных изделий по выходному параметру y. Приемлемого для практики значения процента выхода годных изделий можно добиться путемпутём изменения номинальных значений параметров элементов, вида функции связи входных и выходных параметров, т.е. структуры РЭУ, характеристик отклонений и допусков параметров элементов.

Такие задачи эффективно решаются методом вероятностного моделирования. При этом математической моделью не учитываются временные изменения характеристик модели (вида математического выражения или ее коэффициентов). Реализация метода включает следующие этапы:

моделирование параметров элементов в соответствии с их законами распределения; если параметры элементов зависимы, то получение их случайных значений должно выполняться согласно условным законам распределения. Эта задача решена и описана в литературе применительно к коррелированным параметрам, распределеннымраспределённым по нормальным законам;

многократное вычисление значений выходного параметра для комбинации случайных значений параметров элементов;

статистическую обработку результатов моделирования, которая позволяет:

1) построить гистограмму и подобрать закон распределения выходного параметра;

2) рассчитать вероятность попадания выходного параметра в заданные границы (допуск);

3) рассчитать отклонения выходного параметра, соответствующие заданной вероятности его попадания в полученный диапазон.

 

Число необходимых реализаций N выбирается в зависимости от требуемой точности моделирования.

Пример. Выходной параметр является функцией двух независимых параметров х₁ и х₂ и выражается математической моделью

Y= х₁₊ х₂₊ х₁ × х₂

где	х1 =10В ± 5% - имеет равномерное распределение в пределах поля допуска;
	х2-= 30В ± 10% - имеет нормальное распределение.

 

Требуется получить математические выражения для моделирования случайных параметров х₁ и х₂ и подсчитать значение у в первой реализации процесса (объекта).

Решение.

1. Определяем предельные граничные значения параметра х₁: нижняя граница х_1Н = 9,5В, верхняя - х_1В = 10,5В. Моделируем равномерно распределенныераспределённые значения параметра х₁, используя один из алгоритмов для получения случайной величины, соответствующий закону распределения этой величины[13]. Используя формулу для равномерного распределения получим

x₁=(x_1B – x_1H)×r+x_1H=r+9,5; rÎ(0¼1)

где r – равномерно распределеннаяраспределённая случайная величина в диапазоне 0¼1.

2. Определяем предельные значения параметра х₂. Нижнее отклонение х_2Н = 27В, верхнее предельное отклонение х_2В = 33В. Предполагаем, что все значения х₂ лежат в пределах ±3s(х₂) от номинального значения х_2ном, которое совпадает с математическим ожиданием М(х₂) = х_2ном

Тогда математическое ожидание равно М(х₂) = 30В. Пользуясь "правилом трех сигм", вычисляем среднее квадратическое отклонение параметра х_2. Получим

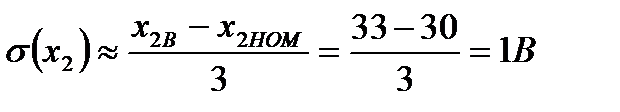
Моделировать значения параметра х₂ с нормальным распределением в найденных пределах от 27 до 33 В можно по формуле

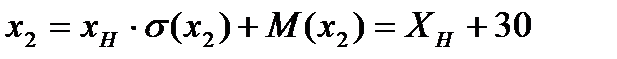
где Х_H — нормально распределенныераспределённые случайные числа с параметрами т = 0, s = 1.

-3£Х_Н£+3

3. Предположим, что моделирование первых значений последовательности равномерно распределенныхраспределённых в интервале (0...1) чисел г и нормальных стандартных чисел Х_Н дало:

r = 0,307; Х_H = -0,460.

По этим значениям вычисляем х₁ и х₂. Получим х₁ = 9,807 В; х₂ = 29,54 В.

Подставляем результаты в модель входного параметра и получаем первое значение выходного параметра у⁽¹⁾ = 329,046.

Аналогично могут быть получены значения выходного параметра у для других реализаций процесса (объекта).

В рассматриваемом примере комбинация случайных параметров х₁ и х₂, а также значение выходного параметра у с целью иллюстрации были получены путемпутём ручного расчетарасчёта. В реальных ситуацияхвесь процесс моделирования проводится с использованиемЭВМ.

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: