 |
Раздел 9 Устойчивость системы
|
|
|
|
Устойчивость системы – это свойство возвращаться к состоянию установившегося равновесия, после устранения возмущения, нарушившего равновесие.
Устойчивость является необходимым условием работоспособности системы.
Система неустойчива, если после снятия возмущения выходная величина неограниченно удаляется от первоначально установившегося режима.
Если график переходного процесса сходящийся, то система устойчива, а если расходящийся то система неустойчива.
Устойчивость системы характеризуется ее свободными движениями. Свободные движения системы описываются однородными дифференциальными уравнениями, т.е. уравнениями без правой части. Для определения устойчивости системы исследуется уравнение. Встречаются различные комбинации корней.
Если характеристическое уравнение имеет только вещественные и неравные корни, то с течением времени система будет удаляться от положения равновесия, т.е. будет неустойчивой.
Если характеристическое уравнение имеет пару комплексных сопряженных корней, то процесс будет затухать. При наличии пары чисто мнимых корней в системе возникают незатухающие гармонические колебания, система находится на границе устойчивости.
Если характеристическое уравнение имеет один нулевой корень, а все остальные корни вещественные и отрицательные, то система имеет множество состояний равновесия.
Для устойчивости необходимо, чтобы все вещественные корни характеристического уравнения были отрицательны, а комплексные корни имели отрицательную вещественную часть.
Определим амплитудно-частотные характеристики звеньев и системы в целом. Передаточная функция объекта регулирования определяется выражением
|
|
|
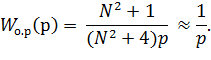
Для определения частотной характеристики объекта регулирования произведем замену в передаточной функции объекта

Получим частотную характеристику объекта регулирования (рисунок 10)


Рисунок 12 - Характеристика частотная объекта регулирования
Определим частотную функцию датчика

Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:

Далее определим модуль, полагая, что



Построим график с учетом выражения


Рисунок 13 - Функция частотная датчика
Определим спектральную характеристику исполнительного механизма

Произведем замену в передаточной функции исполнительного механизма




Рисунок 14 - Характеристика спектральная исполнительного механизма
Определим спектральную характеристику регулятора.
Передаточная функция имеет вид

Примем  и получим
и получим

Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:

Выделим действительную и мнимую части:

Определим модуль, полагая, что



Построим график с учетом выражения


Рисунок 15 - Характеристика спектральная регулятора
Определим частотную характеристику обратной связи – ДРИМ.
Имеем передаточную функцию


Рисунок 16 – Характеристика частотная обратной связи – ДРИМ
Частотную характеристику всей системы можно записать выражением

Устойчивость системы определим по положению корней p1 и p2 из уравнения



По критерию Ляпунова, если характеристическое уравнение имеет пару комплексных сопряженных корней, то процесс будет затухать. Следовательно, наша система не устойчива.
|
|
|


