Главная | Обратная связь | Поможем написать вашу работу!

Преобразование Лапласа. Условие существования, ограничения, основные теоремы операторного метода

Операторный метод расчета переходных процессов в линейных электрических цепях

Классический метод расчета обладает несомненными достоинствами, обусловленными физической наглядностью связей между величинами, которые выражаются дифференциальными уравнениями Кирхгофа, и сравнительной простотой их совместного решения. Часто, однако, задачи при решении классическим методом приводят к громоздким выкладкам, связанным, главным образом, с отысканием постоянных интегрирования, причем, эта процедура усложняется с ростом порядка цепи.

Отмеченные недостатки отсутствуют при применении операторного метода, в соответствии с которым уравнения переходного процесса в линейных цепях, представляющие собой линейные дифференциальные уравнения с постоянными коэффициентами, можно интегрировать операторным методом, основанном на преобразовании Лапласа.

Идея операторного метода заключается в замене вещественной переменной t комплексной переменной , осуществляемой в соответствии с функциональным преобразованием Лапласа. При этом каждой временной функции 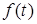, называемой оригиналом (прообразом), ставится в соответствие функция , именуемая изображением (образом). Эта операция записывается f (t)_· = ^· F (p). В результате такой замены система дифференциальных уравнений для оригиналов преобразуется в систему алгебраических уравнений для их изображений. В результате решения этой системы определяют изображение искомой величины, а на заключительном этапе переходят к физически понятной функции – оригиналу .

Подобный прием применялся при анализе стационарного решения цепей символическим методом. Однако в то время, как символический метод можно применять лишь к гармоническим функциям, операторный метод обладает значительно большей общностью и применим к широкому классу функций.

Преобразование Лапласа. Условие существования, ограничения, основные теоремы операторного метода

. (4.27)

Функция (4.27) называется интегралом Лапласа, который ставит в соответствие оригиналу f (t) операторное изображение F (p), т.е. f (t)_· = ^· F (p).

Поскольку это несобственный интеграл, то надо оговорить условия его сходимости:

· функция f (t) должна отвечать условиям Дирихле;

· функция f (t) ограничена, т.е. при она конечна или если и растет по модулю, то не быстрее некоторой экспоненциальной функции , где A и a – положительные числа, т.е. .

В этом случае интеграл Лапласа сходится, т.е. имеет конечное значение при условии, что .

Итак, всегда можно выбрать достаточно большое , не уточняя какое именно, так, что F (p) в полуплоскости является однозначной функцией, т.е. интеграл Лапласа существует в области .

Основным достоинством преобразования Лапласа является его простая связь с частотным спектром функции f (t), широко используемом в теории и современной технике. В преобразовании Лапласа обычно подразумевают, что интервал интегрирования начинается с момента возмущения t = 0⁺, так что оно не отражает особенностей функции в точке t = 0.

Преобразование Лапласа может учитывать изменение физической величины в точке t = 0, если его представить в форме

. (4.28)

Выбор нижнего предела удобен, т.к. при этом учитываются особенности изменения воздействия и реакции в t = 0, когда они содержат импульсную составляющую, а также при использовании начальных условий (0^–), которые задаются формулировкой задачи.

Теоремы операторного метода

1) теорема об однозначном соответствии: f (t)_· = ^· F (p) и F (p)_· = ^· f (t);