 |
Кольцо многочленов над областью целостности.
|
|
|
|
Глава XI. Многочлены.
Кольцо многочленов от одной переменной над
Ассоциативно-коммутативным кольцом с единицей
Определение 1. Пусть K - ассоциативно-коммутативное кольцо с единицей.  Многочленом над кольцом K от переменной x называется выражение вида
Многочленом над кольцом K от переменной x называется выражение вида  , где ai Î K, причем лишь конечное число элементов ai ≠0.
, где ai Î K, причем лишь конечное число элементов ai ≠0.
ai называется коэффициентом многочлена f (x) при степени i.
Множество всех многочленов над кольцом K от переменной x обозначается K [ x ].
Определение 2. Пусть f (x) и g (x)  , где K – ассоциативно-коммутативное кольцо с единицей. Многочлены f (x) и g (x) называются равными (алгебраически), если соответственно равны их коэффициенты при одинаковых степенях x.
, где K – ассоциативно-коммутативное кольцо с единицей. Многочлены f (x) и g (x) называются равными (алгебраически), если соответственно равны их коэффициенты при одинаковых степенях x.
Определение 3. Нулевым многочленом называется многочлен, все коэффициенты которого равны 0, и обозначается 0=0(x).
Определение 4. Пусть K - ассоциативно-коммутативное кольцо с единицей, f (x)  , f (x)≠0(x). Число n называется степенью многочлена f и обозначается deg f =n, если an ≠0 и ai =0 при i > n.
, f (x)≠0(x). Число n называется степенью многочлена f и обозначается deg f =n, если an ≠0 и ai =0 при i > n.
По определению полагают, что степень нулевого многочлена равна  , т.е. deg 0 (x)
, т.е. deg 0 (x) 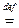
 .
.
Таким образом, если  , то deg
, то deg  (deg
(deg 
 ℕ
ℕ  {0}).
{0}).
Согласно определению 2, добавляя или отбрасывая слагаемые с нулевыми коэффициентами, мы получаем многочлен, равный данному. Таким образом, всякий многочлен степени n может быть записан в виде
 (
( ).
).
Тогда a0 называется свободным или постоянным членом многочлена f (x), an - старшим коэффициентом многочлена f (x).
Определение 5. Пусть K - ассоциативно-коммутативное кольцо с единицей,  ,
,  , причем n ≥ m.
, причем n ≥ m.
Операции сложения и умножения многочленов из K [ x ] определяются по правилам
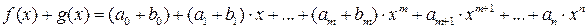 (1)
(1)

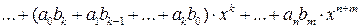 (2)
(2)
Теорема 1. Пусть K – ненулевое ассоциативно-коммутативное кольцо с единицей. Тогда K [ x ] относительно операций по правилам (1) и (2) – также является ассоциативно-коммутативным кольцом с единицей 1(x) = 1.
|
|
|
Доказательство. Проверим для K [ x ] все аксиомы ассоциативно-коммутативного кольца с единицей.
1. K [ x ]¹Æ, например, 0(x)Î K [ x ], так как все его коэффициенты равны 0Î K.
2. Операции «+» и «⋅» по правилам (1) и (2) являются алгебраическими на K [ x ] (т.е. K [ x ] замкнуто относительно этих операций). Действительно, пусть f (x)и g (x)Î K [ x ], из формул (1) и (2) следует, что коэффициенты многочленов f (x) +g (x)и f (x) ⋅g (x)получаются путем сложения и умножения коэффициентов f (x)и g (x), т.е. элементов из K. В силу замкнутости кольца K относительно сложения и умножения, коэффициенты многочленов f (x) +g (x)и f (x) ⋅g (x) принадлежат K. То есть f (x) +g (x)Î K [ x ]и f (x) ⋅g (x)Î K [ x ].
3. <K [ x ], +> - абелева группа.
а) «+» ассоциативно на K [ x ]: " f (x) ,g (x) ,h (x)Î K [ x ] (f (x)+ g (x))+ h (x) =f (x)+(g (x)+ h (x))
б) «+» коммутативно на K [ x ]: " f (x) ,g (x)Î K [ x ] f (x)+ g (x) =g (x)+ f (x)
в) Существует 0(x)=0+0⋅ x +0⋅ x 2+…+0⋅ xn +… Î K [ x ] такой, что "  Î K [ x ]:
Î K [ x ]:  =
= 
аналогично, 
г) "  Î K [ x ] существует
Î K [ x ] существует  Î K [ x ] такой, что
Î K [ x ] такой, что
 = 0+0⋅ x +0⋅ x 2+…+0⋅ xn= 0(x). Аналогично
= 0+0⋅ x +0⋅ x 2+…+0⋅ xn= 0(x). Аналогично  = 0(x).
= 0(x).
4. В K [ x ] выполняются дистрибутивные законы:
д) " f (x) ,g (x) ,h (x)Î K [ x ] (f (x)+ g (x))⋅ h (x) =f (x) ⋅h (x)+ g (x)⋅ h (x)
h (x) ⋅ (f (x)+ g (x)) =h (x) ⋅f (x)+ h (x)⋅ g (x)
Таким образом, K [ x ] – кольцо.
5. Покажем, что K [ x ] – асcоциативно-коммутативное кольцо с 1.
е) «⋅» ассоциативно на K [ x ]: " f (x) ,g (x) ,h (x)Î K [ x ] (f (x)⋅ g (x))⋅ h (x) =f (x)⋅(g (x)⋅ h (x))
ж) «⋅» коммутативно на K [ x ]: " f (x) ,g (x)Î K [ x ] f (x)⋅ g (x) =g (x)⋅ f (x)
з) В K [ x ]существует единичный многочлен 1(x)= 1+0⋅ x +0⋅ x 2+…+0⋅ xn+… Î K [ x ]c коэффициентами b 0=1, bi =0 для остальных i. "  Î K [ x ]
Î K [ x ]

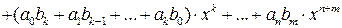 =
=



справедливость а), б), д), е), ж) следует из того, что операции «+» и «⋅» над многочленами сводятся к соответствующим операциям над их коэффициентами – элементами из K, а в кольце K «+» и «⋅» коммутативны, ассоциативны и выполняются дистрибутивные законы.
|
|
|
Теорема доказана.
Степень многочлена. Свойства степени многочлена
Теорема 2. Пусть K – ненулевое ассоциативно-коммутативное кольцо с единицей,  ,
, 

 . Тогда:
. Тогда:
1) deg ( +
+ 
 max{deg
max{deg  , deg
, deg  };
};
2) deg ( ·
·  )
)  deg
deg  + deg
+ deg  .
.
Доказательство.
Пусть  ,
,  . Пусть, например, m
. Пусть, например, m  n. Тогда:
n. Тогда:
1) f (x)+ g (x)= 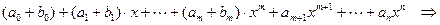
deg (f +g)  max{deg f (x), deg g (x) }=n.
max{deg f (x), deg g (x) }=n.
2) f (x) ⋅g (x)= 
deg (f (x) ⋅g (x))  n+m=deg f (x) + deg g (x) (если
n+m=deg f (x) + deg g (x) (если  и
и  - делители 0, то
- делители 0, то 
 =0
=0
deg f (x) ⋅g (x) < m+n). Теорема доказана.
Следствие 2.1. Пусть K - область целостности.
Тогда deg (f (x) ⋅g (x)) = deg f (x) + deg g (x),  f (x) ,g (x)
f (x) ,g (x) 
 .
.
Кольцо многочленов над областью целостности.
|
|
|


