Теорема о делении с остатком для многочленов

Теорема 6 (о делении с остатком для многочленов) Пусть F – поле, f (x), g (x) F [ x ], g (x) 0. Тогда существуют единственные многочлены q (x), r (x) F [ x ] такие, что f (x) =g (x) ·q (x) +r (x), причем deg r (x) <deg g (x)(1).

При этом q (x) · называется неполным частным, а r (x) – остатком при делении f (x)на g (x).

Доказательство. 1. Существование.

Если f (x)=0, (1) примет вид 0 (x) =g (x) ·0 (x) +0 (x) q (x)=0, r (x)=0, причем
deg r (x)= − < deg g (x) 0.

Если deg f (x)< deg g (x) справедливо f (x) =g (x) ·0 (x) +f (x) в (1) достаточно взять q (x)=0, r (x)= f (x), причем deg r (x)= deg f (x)< deg g (x).

Пусть f (x) 0 и deg f (x) 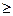deg g (x). Тогда f (x) =a_o+a₁x+…+a_nxⁿ, g (x) =b_o+b₁x+…+b_mx^m и n 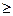m. Доказательство проведем методом математической индукции по параметру n.

1) Пусть n = deg f (x) = 0 f (x) =a₀. Так как m ≤ n=0 и m=deg g (x)¹-¥, то m =0Þ g (x) =b ₀ Так как F – поле и b ₀¹0, то существует b ₀^-1Î F. Тогда , причем deg r (x) = − <0 =deg g (x).

2) Предположим, что утверждение верно для любого многочлена степени, меньшей n, то естьлюбой многочлен степени, меньшей n, имеет представление вида (1), то есть делится на g (x) c остатком.

3) Докажем утверждение для многочлена степени n. Рассмотрим многочлен h (x) =f (x) - b_m^-1∙a_nx^n-m⋅g (x) = (a_o+…+a_nxⁿ) - b_m^-1∙a_nx^n-m⋅ (b_o+…+b_mx^m)=
a_o+…+a_nxⁿ- b₀b_m^-1a_nx^n-m -…-b_mb_m^-1a_nx^mx^n-m= a_o+…+a_nxⁿ- b₀b_m^-1a_nx^n-m -…- a_nxⁿ.

Таким образом, старший член степени n многочлена h (x) уничтожается, и h (x) - многочлен степени, меньшей n. По предположению индукции, h (x) делится на g (x) с остатком, то есть
q₁ (x), r₁ (x) F [ x ]: h (x) =g (x) ∙q₁ (x) +r₁ (x), где deg r₁ (x) <deg g (x)

f (x) -b_m^-1∙a_nx^n-m⋅g (x) =g (x) ∙q₁ (x) +r₁ (x) , причем deg r (x) <deg g (x). Значит, для f (x) существует деление на g (x) с остатком вида (1).

Из 1)-3) по методу математической индукции следует, что утверждение верно .

2. Единственность. Пусть

f (x) =g (x) ∙q₁ (x) +r₁ (x) (1) и

f (x) =g (x) ∙q₂ (x) +r₂ (x) (2).

Покажем, что q₁=q₂, r₁=r₂. Вычтем из равенства (1) равенство (2):
0= g (x)(q₁-q₂) + (r₁-r₂) r₂-r₁=g (x)(q₁-q₂) (3).

Допустим, что q₁-q₂ 0. Согласно теореме 3, F [ x ] - область целостности. Поэтому в F [ x ]нет делителей нуля и из (3) следует, что . Тогда, с одной стороны,

deg (r₂-r₁) 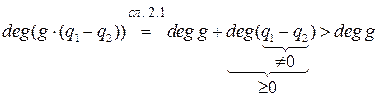, т.е. .

С другой стороны, , т.е.
deg (r₂-r₁) <deg g.

Противоречие. Следовательно, . Значит, .

Теорема доказана.

8. Алгоритм Евклида. НОД и НОК многочленов.

Линейное представление НОД.

Определение 10. Пусть F – поле, f (x), g (x) F [ x ]. Многочлен d (x) F [ x ] называется наибольшим общим делителем многочленов f (x)и g (x) (или коротко, НОД f (x)и g (x)) и обозначается d (x)=(f (x), g (x)), если выполняются два условия:

1) d (x) – общий делитель многочленов f (x)и g (x), т.е. и ;

2) d (x) кратен любому общему делителю многочленов f (x)и g (x), т.е. если и , то .

Определение 11. Пусть K – ассоциативно-коммутативное кольцо с единицей. Элементы a и b кольца K называются ассоциированными в K и обозначаются a ∼ b, если и .

Лемма 1. Пусть F – поле, f (x), g (x) F [ x ]. Тогда
f (x) ∼g (x)Û $ eÎ F ^#: f (x) =e⋅g (x).

Лемма 2. Пусть F – поле, f (x), g (x) ,q (x) ,r (x) F [ x ], g≠0, и f=g·q+r (1). Тогда НОД многочленов f и g и НОД многочленов g и r ассоциированы, т.е. (f,g) ∼ (g,r).

Доказательство. Пусть d₁ =(f, g), d₂ =(g, r).

Так как и , то из (1) Þ и d ₁ – общий делитель g и r 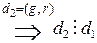(2)

Так как и , то из (1) Þ и d ₂ – общий делитель f и g (3).

Из (2) и (3) следует, что d₁ ∼ d₂. Лемма доказана.

Лемма 3. НОД двух многочленов определяется однозначно с точностью до ассоциированности.

Алгоритм Евклида для нахождения НОД многочленов f и g.

Пусть F – поле, f (x), g (x) F [ x ], g (x)≠0.

Делим с остатком f на g; если остаток r₁ ≠0, то делим с остатком g на r₁, и т.д. (каждый раз делим делитель на остаток):

(4.1)

(4.2)

(4.3) (4)

...

(4. k)

(4. k +1)

Последовательность равенств (4) называется алгоритмом Евклида.

Покажем, что процесс деления в алгоритме Евклида является конечным, то есть через конечное число k шагов очередной остаток r_{k +1}=0. Рассмотрим последовательность (5).

Так как (5) – убывающая последовательность целых неотрицательных чисел, она является конечной и содержит число членов . Следовательно, процесс деления с остатком в алгоритме Евклида (4) конечен и через конечное число k шагов будет получен очередной остаток r_{k +1} такой, что deg r_{k +1}<0. То есть, r_{k +1}=0.

Пусть r_k - последний отличный от нуля остаток. Покажем, что (f,g) ∼ r_k. Действительно, из равенств (4) по лемме 2 получим

(f,g) ∼ (g, r₁ ) ∼ (r₁, r₂ ) ∼…∼ (r_k-1, r_k) ∼ r_k.

Значит, НОД многочленов f и g ассоциирован с последним ненулевым остатком в алгоритме Евклида (4).

Замечание. Так как по лемме 3 НОД двух многочленов определяется однозначно с точностью до ассоциированности, то существует множество ассоциированных между собой НОД, отличающихся, согласно лемме 1, лишь скаляром eÎ F ^#. Из всех возможных НОД выберем тот, который нормирован, т.е. имеет старший коэффициент 1, и будем обозначать его далее через (f,g) или НОД (f,g).

Т.е. НОД многочленов f и g равен нормированному последнему ненулевому остатку в алгоритме Евклида (4).

Определение 12. Пусть F – поле, f (x), g (x) F [ x ]\{0(x)}. Многочлен m (x) F [ x ] называется наименьшим общим кратным многочленов f (x)и g (x) (или коротко, НОК f (x)и g (x)) и обозначается m (x)=[ f (x), g (x)], если выполняются два условия:

1) m (x) – общее кратное многочленов f (x)и g (x), т.е. и ;

2) m (x) делит любое общее кратное многочленов f (x)и g (x), т.е. если и , то .

Лемма 4. НОК двух многочленов определяется однозначно с точностью до ассоциированности.

Теорема 9. Пусть F – поле, f (x), g (x) F [ x ] \{0(x)}. Для нахождения НОК многочленов f и g справедлива следующая формула: [ f, g ]= .

Теорема 10 (теорема о линейном представлении НОД). Пусть F – поле, f (x), g (x) F [ x ], g≠0, d= (f,g). Тогда

(6) – линейное представление НОД f (x)и g (x).

Доказательство. Рассмотрим алгоритм Евклида (4). Выражая из последнего равенства (4) и заменяя их значениями из предыдущих равенств (4), через конечное число шагов получим 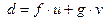, где .

Теорема доказана.

Аналогично определениям 10 и 11 можно дать определение НОД и НОK произвольного конечного количества многочленов f ₁, f ₂, …, f_n F [ x ]. Для их нахождения используется теорема

Теорема 11. Пусть F – поле, f ₁, f ₂, …, f_n F [ x ] \{0(x)}. Для нахождения НОД и НОK многочленов f ₁, f ₂, …, f_n справедливы формулы:

(f ₁, f ₂, …, f_n)=(…((f ₁, f ₂), f ₃)…, f_n)

[ f ₁, f ₂, …, f_n ]=[…[[ f ₁, f ₂], f ₃]…, f_n ].

9. Деление многочлена на (х-с). Схема Горнера.

Пусть F - поле, f (x) =a ₀ xⁿ+a ₁ x^n-1+a_{n- 1} x+a_n ∈ F [ x ]– многочлен, записанный по убывающим степеням.

Пусть с ∈ F. Разделим f (x) на (х-с). По теореме Безу существует q (x)∈ F [ x ]: f (x) = (x-c) ·q (x) +f (c)(1), где f (c) =r – остаток при делении.Из доказательства теоремы Безу следует, что deg q (x) =n- 1.

Пусть q (x) =b₀x^n-1+b₁x^n-2+…+b_n-2x+b_n-1. Подставим в (1) выражения для f и q:

(2) a₀xⁿ+a₁x^{n -1}+…+a_{n -1}x+a_n= (x-c) · (b₀x^{n -1}+b₁x^{n -2}+…+b_{n -2}x+b_{n -1}) + f (c).

 

 

Приравняем коэффициенты при соответствующих степенях переменной:

a0=b0	b0=a0
a1=b1-b0c	b1=b0c+a1
a2=b2-b1c	b2=b1c+a2
… (3)	… (4)
an – 1=bn –1-bn –2c	bn -1=bn -2c+an -2
an=r-bn –1c	r =bn -1c+an

 

 

Система (4) позволяет разделить многочлен f (x) на (х-с), т.е. получить коэффициенты частного и остаток. Систему (4) удобно записывать в виде схемы, которая называется схемой Горнера.

 

коэффициенты f (x)

 

	a0	a1	a2	…	an -1	an
c	b0= a0	b1=a0c+a1	b2=b1c+a2	…	bn -1=bn -2c+an -2	f (c) =bn -1c+an

 

 

 

коэффициенты q (x)

 

10. Разложение многочлена по степеням (х-с)

Пусть F - поле, f (x)= a₀ xⁿ+a₁x^n-1+…+a_{n -1}x+a_n ∈ F [ x ], c ∈ F. Найдем разложение многочлена f (x) по степеням (x-с), т.е. найдем представление f (x)в виде

f (x) =d₀ (x-c) ⁿ+d₁ (x-c) ^n-1+ d₂ (x-c) ^n-2+…+ d_{n -1} (x-c) +d_n .

Разделим f (x) на (x-c), при этом получим неполное частное q₁ и остаток r₀. Далее, разделим частное q₁ на (x-c)? получим частное q2 r1, и т.д.:

f (x)=(x-c) ·q₁ (x) +r₀, deg q₁ (x)= n -1

q₁ (x)=(x-c) ·q₂ (x) +r₁, deg q₂ (x)= n -2

(1) ….

q_n-2 (x) = (x-c) ·q_{n -1} (x) +r_n-2, deg q_n-1 (x) = n- (n-1) =1

q_n-1 (x) = (x-c) ·q_n (x) +r₁, (где q_n (x) =a₀), deg q_n (x) = n–n=0

 

Из (1) следует, что f (x)=(x-c) q₁+r₀ = (x-c) · ((x-c) ·q₁+r₁)) +r₀ =(x-c) ²q₂+ (x-c) r₁+r₀ =(x-c) ² ((x-c) ·q₃+r₂) + (x-c) ·r₁+r₀ = (x-c) ³q₃+ (x-c) ²r₂+ (x-c) ·r₁+r₀ =…=

=(x-c) ^n-1q_n-1+ (x-c) ^n-2r_n-2+…+ (x-c) ²r₂+ (x-c) r₁+r₀ = (x-c) ⁿa₀+ (x-c) ^n-1r_n-1+…+ (x-c) ²r₂+ (x-c) ·r₁+r₀.

Таким образом, f (x) =a₀ (x-c) ⁿ+r_n-1 (x-c) ^n-1+…+r₂ (x-c) ²+r₁ (x-c) +r₀ (2) - разложение f (x) по степеням (x-c). Формулу (2) удобно получать с помощью схемы Горнера.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: