 |
Предварительное значение коэффициента диаметра.
|
|
|
|




2.6. Ориентировочное значение межосевого расстояния.
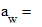

где Kb - коэффициент неравномерности нагрузки;
KV – коэффициент динамической нагрузки.
В предварительных расчетах принимают произведение KbKV=1.1…1.4, мы примем это произведение равным 1.2
T2 – вращающий момент на валу червячного колеса, Нм.
 |
 |
2.7. Предварительное значение модуля, мм.
Значение модуля и коэффициента диаметра согласуется по рекомендации ГОСТ 2144-76 (таблица 28 [2]) с целью уменьшения номенклатуры зуборезного инструмента. Принимаем m = 5.0 и q=10
 |
2.8. Уточняем межосевое расстояние.
Округляем его до ближайшего стандартного значения из ряда: …100;125;160…
Принимаем aw = 125мм.
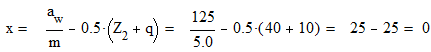 |
2.9. Коэффициент смещения.
2.10. Проверочный расчет по контактным напряжениям.
2.10.1. Угол подъема витка червяка.


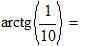
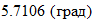
2.10.2. Скорость относительного скольжения в полюсе зацепления, м/с.
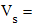
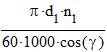
 |
где d1 = m×q = 5.0×10 = 50 (мм)
2.10.3. По скорости скольжения VS выбираем (по таблице 29 [2]) степень точности передачи (8 степень) и определяем коэффициент динамической нагрузки KV=1.25
2.10.4. Коэффициент неравномерности нагрузки.

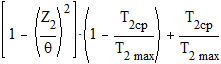
 |
где q - коэффициент деформации червяка, определяемый по таблице 30 [2] в зависимости от q и Z1, равный 108
Ti и ti – вращающий момент и время его действия на i-той ступени по гистограмме нагружения;
Т2ср – среднее значение вращающего момента на валу червячного колеса;
Т2max– максимальный из числа длительно действующих вращающих моментов.
Т2max = 284.461 (Н×м)
 |
Тогда коэффициент неравномерности нагрузки равен:
2.10.5. Расчетные контактные напряжения.
|
|
|
 |

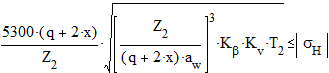
2.11. Проверочный расчет по напряжениям изгиба.
2.11.1. Эквивалентное число зубьев колеса.
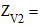
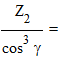


2.11.2. Коэффициент формы зуба колеса выбираем по таблице 31 [2]:


2.11.3. Напряжения изгиба в зубьях червячного колеса.


 |
[sF]2=0.25sT+0.08sB – допускаемые напряжения для всех марок бронз, значения sT и sB приведены в таблице 26 [2]
[sF]2=0.25×245+0.08×530=103.65 (МПа)
Условие прочности выполняется, так как sF2<[sF]2, следовательно, m и q были нами выбраны верно.
2.12. Проверочные расчеты по пиковым нагрузкам.
2.12.1. Проведем проверку по пиковым контактным напряжениям во избежание деформации и заедания поверхностей зубьев.
Условие прочности имеет вид:
|


 |
где [sH]max=2×sT – предел прочности для безоловянистых бронз, [sH]max=2×245=490(МПа)
sH2max<[sH]max, следовательно, условие прочности по пиковым контактным напряжениям выполняется.
2.12.2. Пиковые напряжения изгиба.
Условие прочности по пиковым напряжениям изгиба:


 |
[sF2]max = 0.8×sT = 0.8×245 = 196 (МПа)
sF2max<[sF2]max, следовательно, условие прочности по пиковым напряжениям изгиба выполняется.
2.13. Геометрический расчет передачи.
Основные геометрические размеры червяка и червячного колеса определяем по формулам, приведенным в таблице 32 [2].
Диаметры делительных окружностей для червяка:
d1 = m×q = 5×10 = 50 (мм)
для колеса:
d2 = m×Z2 = 5×40 = 200 (мм)
Диаметры вершин для червяка:
da1 = d1 + 2×m = 50 + 2×5 = 60 (мм)
для колеса:
da2 = d2 + 2×m(1 + x) = 200 + 2×5(1 + 0) = 210 (мм)
Высота головки витков червяка:
ha1 = m = 5 (мм)
Высота ножки витков червяка:
hf1 = 1.2×m = 1.2×5 = 6 (мм)
Диаметр впадин для червяка:
df1 = d1 – 2hf1 = 50 - 2×6 = 38 (мм)
для колеса:
df2 = d2 - 2×m×(1.2 + x) = 200 - 2×5×(1.2 + 0) = 188 (мм)
Длина нарезанной части червяка (формула из таблицы 33 [2]):
|
|
|
b1 = (11 + 0.06×Z2)×m = (11 + 0.06×40)×5 = 67 (мм)
Наибольший диаметр червячного колеса:

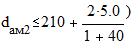
Ширина венца червячного колеса:
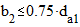

b2 £ 45 мм
Радиус выемки поверхности вершин зубьев червячного колеса:
R = 0.5×d1 – m = 0.5×50 – 5 = 20 (мм)
Межосевое расстояние (проверка):
aw = 0.5×m×(q + Z2 + 2×x) = 0.5×5×(10 + 40 + 2×0) = 125 (мм)
|
|
|


