 |
Определение кратчайших расстояний между пунктами транспортной сети
|
|
|
|
Транспортная есть представляет собой систему дорог (улиц города), которые пригодны по качеству дорожного покрытия, ширине проезжей части, и открыты для движения подвижного состава. Она состоит из отдельных элементов. Ими являются вершины (пункты) и звенья сети. Вершины транспортной сети представляют собой точки на карте города или местности (перекрёстки, пересечения, площади, грузообразующие и грузопоглащающие пункты, микрорайоны), наиболее важные для определения расстояний или маршрутов движения. Каждой вершине присваивается порядковый номер или другое условное обозначение. Две соседние вершины (два соседних пункта) можно соединить линией, по которой осуществляется непосредственная связь между этими вершинами с указанием расстояния между ними. Эти линия называются звеньями сети. Совокупность всех вершин и звеньев называется сетью. Транспортная сеть считается заданной, если определены вершины сети, звенья и их длина.
Расстояния между вершинами или отдельными пунктами транспортной сети определяются путём замера расстояний от каждого пункта до всех остальных по масштабным картам (плану) местности или города, которые затем корректируются путём умножения на коэффициент приведения (1,1÷1,3).
Задача определения кратчайших расстояний является задачей многовариантной, которая имеет множество допустимых решений. Для нахождения оптимального решения применяются математические методы, позволяющие осуществить решения как вручную, так и с использованием современных ЭВМ.
Задача методом потенциалов решается следующим образом:
Шаг 1. Вершина, от которой требуется определить кратчайшие расстояния, называется начальной. Ей присваивается потенциал 
.
|
|
|
Шаг 2. Просматриваются все звенья, начальные вершины 
которых имеют потенциалы 
, а конечные 
– не имеют. Определяется значение потенциалов конечных вершин 
по формуле:
 , (11.1)
|
где 
– длина звена (
), т.е. расстояние между вершинами и .
Из всех полученных потенциалов выбирается наименьший и его значение присваивается соответствующей конечной вершине. Звено () отмечается стрелкой. Шаг 2 повторяется до тех пор, пока всем вершинам данной сети не будут присвоены потенциалы.
Величина потенциалов у соответствующих вершин показывает кратчайшее расстояние от выбранного начального до данного пункта. Звенья со стрелками образуют кратчайший маршрут движения от начального пункта до всех остальных. Принимая за начало сети последовательно каждый её пункт (вершину) и выполняя расчёты по описанному методу, можно получить таблицу кратчайших расстояний между всеми пунктами сети.
Пример. Необходимо определить кратчайшее расстояние от вершины А до всех остальных вершин (пунктов) сети на рисунке 11.1.
Шаг 1. Принимается 
.
Шаг 2.
1) Определяются звенья, для которых вершина А является начальной. На рисунке 11.1 – это звенья АБ, АД, АЕ, АЗ. Вычисляются потенциалы конечных вершин этих звеньев по формуле 1.1:
;
;
;
2) выбирается наименьшее значение этих потенциалов:
3) звено АД отмечается стрелкой. Вершине Д присваивается значение потенциала равное 5.
Потенциалы проставляются в виде квадратов на рисунке 11.1 около соответствующих вершин.
Вновь повторяется шаг 2, но за начальную вершину принимается вершина Д, потенциал которой определён. Теперь можно получить значения потенциалов для вершин Г, Е, Ж:
;
;
.
Из всех полученных сейчас и на первом этапе расчёта значений потенциалов выбирается наименьшее – 
. Это значение проставляется в квадрате у вершины Б. Звено АБ отмечается стрелкой. Теперь в качестве начальной вершины используется вершина Б. Она связана с вершинами В и Г звеньями БВ и БГ. Определяется значение потенциалов для этих вершин:
|
|
|
;
.
Для вершины Г уже было определено раньше значение потенциала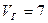 
, которое меньше полученного на данном этапе расчёта значения 
. Следовательно, вершине Г присваивается потенциал, равный 7, а стрелкой отмечается звено ДГ. Аналогично выбирается потенциал для вершин Е: 
. Стрелкой отмечается звено ДЕ.
Далее опять из всех полученных значений потенциалов выбирается наименьшее. Это значение имеет потенциал вершины Г – 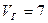. Значит, теперь эта вершина может быть задана как начальная, и на следующем этапе можно определить значение потенциалов вершин В, Ж.
На основании проведённых расчётов может быть составлена таблица кратчайших расстояний между пунктами транспортной сети в таблице 11.1.
Таблица 11.1.
Кратчайшие расстояния между пунктами транспортной сети
| Вершины (пункты) сети | А | Б | В | Г | Д | Е | Ж | З | И | К | Л |
| А | - | ||||||||||
| Б | - | ||||||||||
| В | - | ||||||||||
| Г | - | ||||||||||
| Д | - | ||||||||||
| Е | - | ||||||||||
| Ж | - | ||||||||||
| З | - | ||||||||||
| И | - | ||||||||||
| К | - | ||||||||||
| Л | - |
Рисунок 11.1. Схема транспортной сети.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12.
|
|
|
