 |
Общая задача линейного программирования
|
|
|
|
РЕФЕРАТ
по дисциплине «Экономический анализ и управление производством»
Студент гр. МТП-21-16-01 Д.К. Хасанов
(подпись, дата)
Руководитель канд. экон. наук, доц. О.А. Александрова
(подпись, дата)
| Оценка при защите |
| (подпись) |
| «__»________20__г. |
Уфа
2017
СОДЕРЖАНИЕ
1. Теоретическая часть 3
1.1 Цели и задачи экономического анализа производства 3
1.2 Линейное программирование 4
1.3Общая задача линейного программирования 5
1.4 Геометрическая интерпретация и графический метод решения
задачи линейного программирования 7
1.5 Симплексный метод решения задачи линейного программирования 9
2. Практическая часть 10
Список использованных источников 16
Теоретическая часть
Цели и задачи экономического анализа производства
Общая цель любого экономического анализа – выявление и реализация резервов повышения эффективности деятельности организации.
Задачи экономического анализа:
- изучение и объективная оценка показателей, отражающих эффективность функционирования организации, выявление размера и динамики отклонений от базисных значений показателей;
- диагностика хозяйственных процессов, установление количественных характеристик действия различных факторов на результативность производства;
- выявление резервов повышения эффективности производства; - обоснование принимаемых управленческих решений;
- контроль за деятельностью организации и её подразделений;
- установление экономических закономерностей в развитии организации для стратегического прогнозирования и текущего планирования хозяйственной деятельности.
Оценка, диагностика и анализ состояния исследуемого объекта практически всегда предваряет процесс разработки, принятия, организации выполнения управленческого решения. Экономическая информация о деятельности организации анализируется в динамике и в статике с определением степени влияния на нее объективных и субъективных факторов. Условие правильного анализа – экономически обоснованная классификация причин, влияющих на хозяйственную деятельность и ее результаты. Взаимосвязь и взаимозависимость между отдельными экономическими показателями определяются объективными условиями производства [1].
|
|
|
Линейное программирование
Экономико-математические методы в общем виде делятся на три основные группы:
- экономические (матричные, теория производственных функций, теория межотраслевого баланса);
- методы экономической кибернетики и оптимального программирования (линейное, динамическое, нелинейное программирование);
- методы исследования операций и принятия решений (теория графов, теория игр, теория массового обслуживания).
К общетеоретическим методам относят интуитивные и формализованные методы. При этом к формализованным относят метод экстраполяции и математического моделирования [1].
Термин «линейное программирование» впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному программированию (основные задачи и приложения, критерий оптимальности, экономическая интерпретация, методы решения, геометрическая интерпретация результатов решения) были проведены в конце 30-х годов в СССР в Ленинградском университете Л. В. Канторовичем [2].
Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. По типу решаемых задач методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений [3].
|
|
|
Линейное программирование представляет собой часть раздела математического программирования, занимающуюся разработкой теории и методов решения экстремальных задач, в которых целевая установка (критерий оптимальности) и условия (ограничения) выражаются линейными соотношениями. Другими словами, задачи линейного программирования предполагают выявление цели управления, а также определение критерия, по которому будут сравниваться различные варианты решения. В экономическом анализе такими критериями могут быть: наибольшая прибыль, минимальные затраты на производство продукции, максимальная загрузка оборудования, производительность труда и др. В задачах линейного программирования такие критерии отражаются целевой функцией.
Область применения линейного программирования в анализе и управлении производством достаточно обширна. Наиболее содержательными являются следующие задачи:
1) определение оптимального ассортимента продукции, в котором каждому ее виду свойственны свои издержки и потребности в ресурсах;
2) сведение к минимуму отходов при раскрое материала;
3) определение оптимальных уровней запасов на складе предприятия;
4) составление оптимального графика отгрузки с учетом распределения продукции между производственными предприятиями и складами, складами и магазинами розничной торговли;
5) определение наилучшего пункта местоположения производства путем оценки затрат на транспортировку между альтернативными местами размещения нового предприятия и местами его снабжения и сбыта готовой продукции;
6) минимизация издержек при распределении рабочих по станкам и рабочим местам [4].
Линейное программирование широко применяется в сфере военной деятельности, сельском хозяйстве, промышленности, управлении производственными процессами и запасами, в экономике и на транспорте [3].
Общая задача линейного программирования
|
|
|
Общей задачей линейного программирования (ОЗЛП) называют задачу максимизировать (минимизировать) функцию
| (1) |
при ограничениях: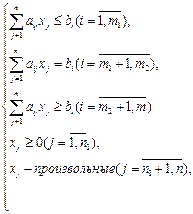 
(2)
где cj, aij, bi -заданные действительные числа, (1) - целевая функция, (2) - ограничения, 
- план задачи.
Экономическая интерпретация модели линейного программирования состоит в следующем. Моделируемая система характеризуется наличием нескольких видов «производственной деятельности»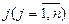 
, для осуществления которых требуются имеющиеся в ограниченном количестве различные ресурсы 
Расход i-го ресурса на единицу продукта j-го вида производственной деятельности равен aij. В свою очередь при таком потреблении результат j-го вида производственной деятельности для единицы соответствующего продукта (удельная стоимость или прибыль) характеризуется величиной cj.
Цель построения модели состоит в определении уровней (объемов производства) каждого вида производственной деятельности xj, при которых оптимизируется (максимизируется или минимизируется) общий результат производственной деятельности системы в целом без нарушения ограничений, накладываемых на использование ресурсов.
Оптимальным решением (или оптимальным планом) задачи ЛП называется решение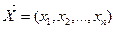 
системы ограничений (1), при котором линейная функция (2) принимает оптимальное значение.
Термины «решение» и «план» - синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическом решении), а второй - о содержательной стороне (экономической интерпретации) [3].
Симметричной формой записи ЗЛП называют задачу
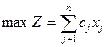
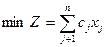
или задачу 
(3)
|
|
|
