 |
Геометрическая интерпретация и графический метод решения задачи линейного программирования
|
|
|
|
Наиболее простым и наглядным методом решения задач линейного программирования является графический метод. Он применяется для задач линейного программирования с двумя переменными, когда ограничения выражены неравенствами, и задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
Графический метод основан на геометрическом представлении допустимых решений и целевой функции задачи. Каждое из неравенств задачи линейного программирования определяет на координатной плоскости (x1, x2) некоторую полуплоскость (рисунок 1). Пересечение этих полуплоскостей задает область допустимых решений (ОДР), то есть любая точка из этой области является решением системы ограничений. Область допустимых решений всегда представляет собой выпуклую фигуру.
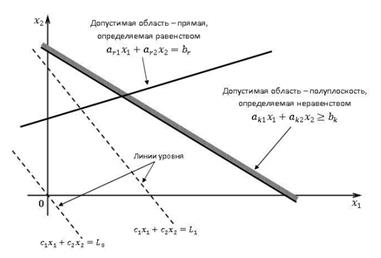
Рисунок 1 - Геометрическая интерпретация ограничений и целевой функции задачи линейного программирования
В общем случае область допустимых решений может быть представлена одной из следующих фигур: выпуклым многоугольником, неограниченной многоугольной областью, лучом, отрезком, точкой или пустой областью. В последнем случае говорят, что ограничения не совместны.
Целевая функция задачи линейного программирования при фиксированном значении L определяет на плоскости прямую линию c1 x1 + c2 x2 = L.
Изменяя значения L, получим семейство параллельных прямых, называемых линиями уровня (рисунок 1).
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из области допустимых решений, на которых достигается самая верхняя (нижняя) линия уровня целевой функции, расположенная дальше (ближе) остальных в направлении наискорейшего роста [5].
|
|
|
Симплексный метод решения задачи линейного программирования
Реальные задачи линейного программирования содержат, как правило, большое число неизвестных. Графическим методом, несмотря на его простоту и наглядность, решить такие задачи невозможно. Поэтому необходимы аналитические методы, позволяющие решать задачи линейного программирования с любым числом переменных.
Универсальным методом решения задач линейного программирования является симплексный метод (симплекс- метод), в основе которого лежит идея последовательного улучшения решения (направленного перебора вершин).
Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины области допустимых решений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум). Для использования симплекс-метода требуется, чтобы система ограничений задачи линейного программирования выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные переменные (базис). Решение задачи распадается на ряд шагов (итераций). На каждом шаге от данного базиса переходят к другому, новому базису с таким расчетом, чтобы значение целевой функции увеличивалось. Для перехода к новому базису из старого базиса удаляется одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис, который доставляет максимум линейной функции, а соответствующее базисное решение является оптимальным либо выясняется, что задача не имеет решения [5].
Практическая часть
Задача 1.
|
|
|
Предприятие ООО "Пшеница" предполагает выпускать два вида продукции: печенье и пряники, для производства которых используется сырьё трех видов: мука, сахар, дрожжи. Производство обеспечено сырьем каждого вида в количествах: 750, 807, 840 кг. На изготовление печенья требуется затратить сырья каждого вида 5, 4, 1 кг, соответственно, а для пряников - 2, 5, 7 кг. Прибыль от реализации печенья составляет 30 ден. ед., для пряников - 49 ден. ед.
Решение.
Занесём необходимые нам данные во вспомогательную таблицу:
Таблица 1 – Исходные данные
| Вид сырья | Продукция | Ограничения по сырью | |
| печенье | пряники | ||
| Мука | |||
| Сахар | |||
| Дрожжи | |||
| Прибыль |
Обеспечим точную формулировку проблемы. Пускай X 1 и X 2 - количество печенья и пряников, запланированных к изготовлению. Так как число материала согласно любому типу ограничено, то обязаны осуществляться соответствующие неравенства:
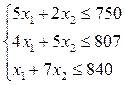
| (4) |
| (5) |
Данная система неравенств считается и концепцией ограничений этой проблемы. Целевая роль (линейная форма), выражающая доход компании, имеет вид:
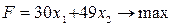
| (6) |
Итак, задача сводится к нахождению максимума функции ограничениях:
|
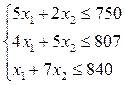
| (7) |
|
| (8) |
Для сведения системы ограничений-неравенств к системе уравнений добавим к левосторонней части каждого неравенства добавочные неотрицательные переменные 
В условиях этой задачи они обладают определенной экономической сущностью, а именно высказывают размер остатков материала каждого типа уже после исполнения проекта согласно выпуску продукта. После внедрения добавочных переменных приобретаем систему уравнений:
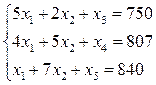
| (9) |
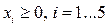
| (10) |
Необходимо отыскать такое возможное базисное решение данной концепции ограничений, которое бы максимизировало линейную форму
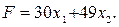
| (11) |
Решая задачу, приходим к следующему выводу.
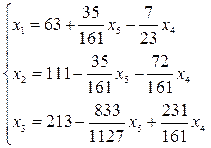
| (12) |
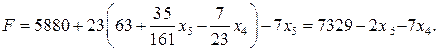
| (13) |
Таким образом, для получения наибольшей прибыли, равной 7329 ден. ед., из данных запасов сырья предприятие должно изготовить 63 кг печенья и 111 кг пряников [6].
Задача 2
Рассмотрим симплекс-метод на примере решения задачи о производстве сыров. Математическая модель этой задачи имеет следующий вид:
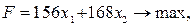
| (14) |
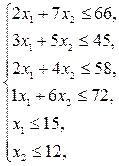
| (15) |
| (16) |
Решение:
Приведем ограничения задачи к каноническому виду, добавив к их левым частям дополнительные неотрицательные переменные x3, x4, x5, x6, x7, x8, и запишем расширенную систему:
|
|
|
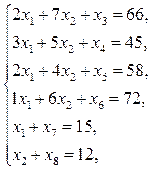
| (17) |
| (18) |
Дополнительные неотрицательные переменные будут базисными, так как каждая из них входит только в одно уравнение системы с коэффициентом единица. Занесем условия задачи в симплексную таблицу 2.
Таблица 2 – Симплексная таблица
| Базисные переменные (БП) | Свободный член, bi | Свободные переменные (СП) | Оценочные отношения | |
| x1 | x2 | |||
| x3 | 66/7 | |||
| x4 | ||||
| x5 | 29/2 | |||
| x6 | ||||
| x7 | - | |||
| x8 | ||||
| F | -156 | -168 |
Выпишем решение из симплексной таблицы 2 и проанализируем его: x1 = x2 = 0 (как небазисные переменные), т.е. комбинат сыр не выпускает. Дополнительные переменные x3 = 66, x4 = 45, x5 = 58, x6 = 72, x7 = 15, x8 = 12 означают количество неиспользованных ресурсов. Поскольку сыр не выпускается, то ресурсы не используются, и, следовательно, прибыль при этом равна нулю (F = 0).
Решение задачи допустимое, так как базисные переменные принимают положительные значения. Переходим к поиску оптимального решения. В строке функции наибольший по абсолютной величине (среди отрицательных) элемент находится во втором столбце, поэтому этот столбец берем за разрешающий и выделяем его цветом (таблица 2). Разрешающую строку находим по наименьшему положительному симплексному отношению:
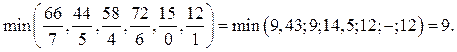
| (19) |
Наименьшее симплексное отношение соответствует второй строке, следовательно, она будет разрешающей. Выделим эту строку в таблице 3 цветом. Разрешающий элемент находится на пересечении разрешающих строки и столбца и равен 5. Рассчитаем элементы новой симплексной таблицы (таблица 3).
Таблица 3 – Симплексная таблица
| Базисные переменные (БП) | Свободный член, bi | Свободные переменные (СП) | Оценочные отношения | |
| x1 | x4 | |||
| x3 | -2,2 | -7/5 | - | |
| x2 | 3/5 | 1/5 | ||
| x5 | -0,4 | -4/5 | - | |
| x6 | -2,6 | -6/5 | ||
| x7 | - | |||
| x8 | -0,6 | -1/5 | ||
| F | -55,2 | 168/5 |
Выпишем решение из таблицы 3:
x1 = 0, x2 = 9, x3 = 3, x4 = 0, x5 = 22, x6 = 18, x7 = 15, x8 = 15, F = 1512 (тыс. руб).
|
|
|
Это решение означает, что комбинат может произвести сыра «Петровский» в объеме 9 тонн, при этом оно получит при- быль в размере 1512 тыс. руб., второй ресурс будет использован полностью (x1 = 0). Решение в таблице 3 не является оптимальным, так как в строке функции имеется отрицательный элемент (-55,2). В соответствии с алгоритмом выберем разрешающий элемент (15) и рассчитаем новую симплексную таблицу (таблица 4). В таблице 4 получено оптимальное решение:
x1 = 15, x2 = 0, x3 = 36, x4 = 0, x5 = 28, x6 = 57, x7 = 0, x8 = 12, F = 2340 (тыс. руб).
Таблица 4 – Симплексная таблица
| Базисные переменные (БП) | Свободный член, bi | Свободные переменные (СП) | Оценочные отношения | |
| x7 | x4 | |||
| x3 | 2,2 | -1,4 | ||
| x2 | -0,6 | 0,2 | ||
| x5 | 0,4 | -0,8 | ||
| x6 | 2,6 | -1,2 | ||
| x1 | ||||
| x8 | 0,6 | -0,2 | ||
| F | 55,2 | 33,6 |
Из решения видно, что сыр «Нежный» с меньшей прибылью (156 тыс. руб./т) по сравнению с сыром «Петровский» вошел в оптимальное решение задачи. Это связано с тем, что у этого вида сыра низкая норма расхода второго ресурса. Поэтому переход на выпуск только сыра «Нежный» позволило увеличить прибыль по сравнению с предыдущим решением на 828 тыс. руб [5].
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Экономический анализ и управление производством: учебное пособие/М.А.Евдокимова, А.Е. Михайлова.- СПб.: СПбГЛТУ, 2013.- 118 с.
2. Экономико-математические методы: учебное пособие/В.А. Клетин – М.: ММОИ, 2012.- 38 с.
3. Математическое программирование: учебное пособие/ А.В. Кузнецов– М.: Высшая школа, 1976. – 352 с.
4. Краткий курс лекций по дисциплине «Теория экономического анализа» / [Электронный ресурс] – URL: http://studme.org/53272/ekonomika/ekonomiko-matematicheskie_metody_analize. Дата обращения 27.03.2017.
5. Математические модели в экономике: учебное пособие / И.А. Печерских, А.Г. Семенов; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2011. – 191 с.
6. Методы линейного программирования при решении экономических задач / Д.А. Каримова / СГАУ. – Ставрополь, 2016. – 101 с.
|
|
|
