 |
Системы массового обслуживания с отказами
|
|
|
|
УДК 519.872
Методические указания к практическому занятию «Системы массового обслуживания» по дисциплинам «Исследование операций», «Экономико-математические методы» для студентов специальностей: 7.050201 – «Менеджмент организаций», 7.050107 – «Экономика предприятия» всех форм обучения / Сост. Н.А. Русина, А.А. Загорулько – Севастополь: Изд-во СевНТУ, 2006г. – 16с.
Методические указания подготовлены с целью закрепления теоретических знаний и получения практических навыков в области систем массового обслуживания. Методические указания предназначены для студентов экономических специальностей всех форм обучения.
Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов (протокол № 9 от «11»апреля 2006г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний
Рецензент:
Андреева Л.И., доцент кафедры «Экономика и маркетинг»
СОДЕРЖАНИЕ
1. Цель работы.....................................................................................................4
2. Теоретическая часть........................................................................................4
2.1. Общее понятие систем массового обслуживания…….............................4
2.2. Системы массового обслуживания с отказами….....................................5
2.3. Системы массового обслуживания с ожиданием…..................................8
3. Индивидуальные задания.............................................................................10
4. Содержание отчета........................................................................................14
5. Контрольные вопросы...................................................................................14
Библиографический список..............................................................................15
ЦЕЛЬ РАБОТЫ
Закрепление теоретических знаний и получение практических навыков в области систем массового обслуживания.
|
|
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общее понятие систем массового обслуживания
В производственной деятельности и повседневной жизни часто возникают такие ситуации, когда появляется необходимость в обслуживании требований или заявок, поступающих в систему. Иногда системы обслуживания обладают ограниченными возможностями для удовлетворения спроса, и это приводит к образованию очередей. Примерами подобных явлений могут быть очереди в магазинах, билетных кассах, скопление самолетов над аэродромами [1].
Задачами теории массового обслуживания являются анализ и исследование явлений, возникающих в системах обслуживания. Одна из основных задач теории заключается в определении таких характеристик системы, которые обеспечивают заданное количество функционирования, например, минимум времени ожидания, минимум средней длины очереди и т.д. Общей особенностью задач, связанных с массовым обслуживанием является случайный характер исследуемых явлений. Количество требований на обслуживание, временные интервалы между их поступлениями и длительность обслуживания случайны. Поэтому основным аппаратом описания систем обслуживания оказывается аппарат теории случайных процессов, в частности марковских [3].
Всякой системе массового обслуживания характерна структура, которая определяется составом элементов и функциональными связями. Основные элементы системы следующие: входящий поток требований, каналы обслуживания, очередь требований и выходящий поток требований.
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим (пуассоновским).
Простейший поток обладает тремя основными свойствами: ординарности, стационарности и отсутствием последействия.
|
|
|
Ординарностьпотока означает практическую невозможность одновременного поступления двух и более требований. Например, достаточно малой является вероятность того, что из группы станков, обслуживаемых бригадой ремонтников, одновременно выйдут из строя сразу несколько станков.
Стационарнымназывается поток, для которого математическое ожидание числа требований, поступающих в систему в единицу времени (обозначим λ,), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени ∆tзависит от его величины и не зависит от начала его отсчета на оси времени.
Отсутствие последействияозначает, что число требований, поступивших в систему до момента t,не определяет того, сколько требований поступит в систему за промежуток времени от tдо t+ ∆t.
Например, если на ткацком станке в данный момент произошел обрыв нити, и он устранен ткачихой, то это не определяет, произойдет новый обрыв на данном станке в следующий момент или нет, тем более это не влияет на вероятность возникновения обрыва на других станках.
Каждой из систем массового обслуживания свойственна определенная организация. По составу системы обслуживания бывают одноканальные и многоканальные. Многоканальные системы могут состоять из приборов как одинаковой, так и разной производительности [2].
Другой признак классификации время пребывания требований в системе до начала обслуживания. По этому признаку все системы можно делить на три группы: системы с неограниченным временем ожидания, системы с отказами (с потерями) и системы смешанного типа.
Системы массового обслуживания с отказами
Имеется n каналов, на которые поступает поток заявок с интенсивностью λ.Поток обслуживаний имеет интенсивность µ и время обслуживания одной заявки tобсл.Найти предельные состояния системы и показатели её эффективности.
Система S имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе):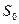 
, 
, 
,..., 
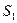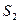, где - состояние системы, когда в ней находятся nзаявок [4].
Для расчета такой системы используются следующие показатели:
|
|
|
- интенсивность обслуживания (производительность):
μ=1/ tобсл (1)
- интенсивность нагрузки канала:
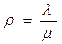(2)
- вероятность нахождения системы в состоянии 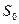(свободном):
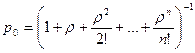(3)
- вероятность нахождения системы в других состояниях:
, 
, …, 
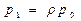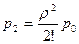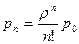(4)
- вероятность отказа СМО:
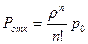(5)
- относительная пропускная способность:
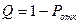(6)
- абсолютная пропускная способность:
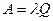(7)
- средне число занятых каналов:
(8)
Рассмотрим пример решения задачи многоканальной СМО с отказами.
Задача № 1. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 (заявок/час). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.
Решение. По условию n=3, λ=0,25 (заявок/час), tобсл = 3 (ч). Определим интенсивность потока обслуживаний:
μ =1/ tобсл =1/3=0,33 (заявок/час)
Вычислим интенсивность нагрузки ЭВМ по формуле (2):
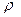=0,25 / 0,33 = 0,75
Найдем предельные вероятности состояний:
- вероятность нахождения системы в свободном состоянии определяется по формуле (3):
= (1+0,75+0,75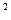 
/2!+0,75 
/3!)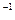 
= 0,476
По формуле (4) определим вероятности нахождения системы в других состояниях.
- вероятность того, что занята только одна ЭВМ:
= 0,75 ∙ 0,476 = 0,357
- вероятность того, что заняты 2 ЭВМ:
=(0,75 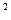/2!) ∙ 0,476 = 0,134
- вероятность того, что все 3 ЭВМ заняты, т.е. вероятность отказа:
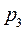=(0,75 /3!) ∙ 0,476 = 0,033
Таким образом можно сделать вывод о том, что в стационарном режиме работы вычислительно центра в среднем 47,6 % времени нет ни одной заявки, 35,7% - имеется одна заявка (занята одна ЭВМ), 13,4 %- две заявки (две ЭВМ), 3,3 % времени – три заявки (заняты три ЭВМ).
Вероятность отказа (когда заняты все три ЭВМ), таким образом, P 
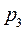= =0,033.
|
|
|
По формуле (6) определяется относительная пропускная способность центра:
Q = 1 – 0,033 = 0,967
Т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.
По формуле (7) вычисляется абсолютная пропускная способность центра:
А = 0,25 ∙ 0,967 = 0,242
В один час в среднем обслуживается 0,242 заявки.
По формуле (8) рассчитывается среднее число занятых ЭВМ:
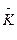= 0,242 / 0,33 = 0,725
Каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5\3=24,2%.
При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих ЭВМ (с одной стороны, у нас высокая пропускная способность СМО, а с другой стороны – значительный простой каналов обслуживания) и выбрать компромиссное решение.
|
|
|
