Главная | Обратная связь | Поможем написать вашу работу!

Системы массового обслуживания с ожиданием

⇐ ПредыдущаяСтр 2 из 2

Имеется n-канальная СМО с неограниченной очередью. Она характеризуется следующими показателями [5]:

- предельные вероятности:

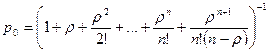(9)

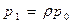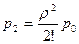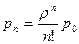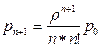, ,..., , (10)

- вероятность того, что заявка окажется в очереди:

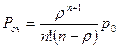(11)

- среднее число занятых каналов:

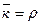(12)

- среднее число заявок в очереди:

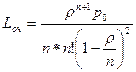(13)

- среднее время нахождения в очереди:

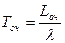(14)

- среднее число заявок в системе:

(15)

- среднее время нахождения заявки в очереди:

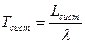(16)

Рассмотрим пример решения задачи многоканальной СМО с ожиданием.

Задача №2. В универсаме к узлу расчета поступает поток покупателей с интенсивностью 81 человек в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя tобсл = 2 мин. Определить предельные вероятности состояний и характеристики обслуживания узла расчета.

Решение. По условию λ=81(чел./час)= 81/60=1,35 (чел./мин.). По формулам (1, 2):

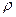= λ/μ= λ * tобсл = 1,35 * 2 = 2,7

Очередь не будет возрастать до бесконечности при условии 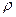/n <1, т.е. при n > 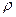= 2,7. Таким образом, минимальное количество контролеров-кассиров n =3.

Найдем характеристики обслуживания СМО при n=3.

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (9):

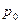= (1+2,7+2,7 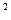/2!+2,7 /3!+2,7 /3!(3-2,7)) 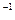= 0,025

В среднем 2,5 % времени контролеры-кассиры будут простаивать.

Вероятность того, что в узле расчета будет очередь, определим по формуле (11):

P 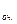= (2,7 /3!(3-2,7))0,025 = 0,735

Среднее число покупателей, находящихся в очереди рассчитывается по формуле (13):

L 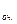= (2,7 /(3*3!(1-2,7/3) 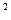))*0,025 = 7,35 (чел.)

Среднее время ожидания в очереди вычисляется по формуле (14):

T 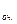=7,35/1,35 = 5,44 (мин.)

Определим среднее число покупателей в узле расчета по формуле (15):

L 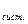=7,35+2,7=10,05 (чел.)

Среднее время нахождения покупателей в узле расчета находится по формуле (16):

T 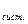=10,05/1,35=7,44 (мин)

Среднее число кассиров, занятых обслуживанием покупателей, по формуле (12) =2,7.

Коэффициент (доля) занятых обслуживанием контролеров-кассиров вычисляется по следующей формуле:

=p/n (17)

=2,7/3=0,9

Абсолютная пропускная способность узла расчета A=1,35 (чел./мин), или 81 (чел./час), т.е. 81 покупатель в час. Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров – кассиров.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

В качестве индивидуального задания студенту необходимо самостоятельно решить задачу в соответствии с выбранным вариантом.

Выбор варианта для выполнения индивидуального задания осуществляется при помощи таблицы 1.

Таблица 1 – Выбор варианта для индивидуального задания

Студенты, фамилия которых начинается с буквы

Номер варианта задач для нечётной последней цифры зач.кн.

Номер варианта задач для чётной последней цифры зач.кн.

Студенты, фамилия которых начинается с буквы

Номер варианта задач для нечётной последней цифры зач.кн.

Номер варианта задач для чётной последней цифры зач.кн.

Задания по вариантам представлены ниже.

Вариант №1

На АЗС имеются две колонки (n=2) для заправки автомобилей. Автомобили подъезжают на АЗС в соответствии с пуассоновским распределением со средней частотой 2 автомобиля за 5 минут (λ=2/5 (авт./мин)). Заправка автомобиля в среднем длится 3 минуты (tобсл=3 мин.), продолжительность заправки распределена по экспоненциальному закону. Требуется определить: 1) вероятность того, что у АЗС не окажется ни одного автомобиля; 2) вероятность того, что обе колонки будут заняты; 3) среднюю длину очереди в ожидании заправки; 4) среднее время ожидания автомобиля в очереди.

Вариант №2

Анализируется работа междугородного переговорного пункта в небольшом городке. Пункт имеет 3 телефонных аппарата для переговоров (n=3). В среднем за сутки поступает 240 заявок на переговоры (λ=240 (заявка/сутки)). Средняя продолжительность переговоров (с учетом вызова абонентов в другом городе) составляет 5 минут (tобсл=5 мин.). Никаких ограничений на длину очереди нет. Поток заявок и обслуживаний -простейшие. Определить предельные вероятности состояний и характеристики обслуживания переговорного пункта в стационарном режиме.

Вариант №3

Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с четырьмя каналами (четыре группы проведения осмотра, n=4). На осмотр и выявление дефектов каждой машины затрачивается в среднем 30 минут (tобсл=30 мин.). На осмотр поступает в среднем 36 машин в сутки (λ=36 (машина/сутки)). Поток заявок и обслуживаний - простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить вероятности состояний и характеристики обслуживания профилактического пункта осмотра.

Вариант №4

В вычислительный центр коллективного пользования с тремя ЭВМ (n=3) поступают заказы от предприятий на вычислительные работы. Если работают все 3 ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 2 часа (tобсл=2 часа). Интенсивность потока заявок 0,2 заявок в час (λ=0,2 (заявка/час)). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Вариант №5

В универсаме работает 3 кассира-контролёра (n=3). К узлу расчета поступает поток покупателей с интенсивностью λ=81 (человек/час). Средняя продолжительность обслуживания контролером кассиром одного покупателя равна 2 минуты (tобсл=2 минуты). Определить показатели эффективности работы системы.

Вариант №6

В филиале банка «Таврика» города Севастополя постоянно работают три оператора (n=3). Если клиент заходит в банк, когда все операторы заняты, то он сразу уходит, не ожидая обслуживания. Среднее число клиентов, обращающихся в банк за 1 час, составляет 24 человека (λ=24 (человек/час)). Среднее время, затрачиваемое оператором на обслуживание одного клиента, составляет 5 минут (tобсл=5 минут). Определить основные характеристики эффективности функционирования данного филиала банка.

Вариант №7

Для уничтожения обнаруживаемых целей противника выделено два подразделения (n=2). Поток заявок на уничтожение целей - простейший, с интенсивностью - λ=0,5 цели/час. Среднее время от момента начала открытия огня по цели до момента готовности подразделения к открытию огня по новой цели равно двум часам (t_обсл=2 часа). Определить эффективность системы, состоящей из двух подразделений, если огонь по цели должен быть открыт немедленно после ее обнаружения.

Вариант №8

Механическая мастерская завода с тремя постами (n=3) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих в мастерскую, - пуассоновский и имеет интенсивность λ=2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательному закону и равно t_обсл=0,5 суток. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно. Определить показатели эффективности системы.

Вариант №9

Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с тремя (n = 3) взаимозаменяемыми ПЭВМ для решения поступающих задач. Поток задач, поступающих на ВЦ, имеет интенсивность λ=1 задаче в час. Средняя продолжительность обслуживания t_обсл=1,8 час. Поток заявок на решение задач и поток обслуживания этих заявок являются простейшими. Определить показатели эффективности системы.

Вариант №10

Ателье по ремонту аппаратуры имеет 5 опытных мастеров (n = 5). В среднем в течение рабочего дня от населения поступает в ремонт 10 аппаратов (λ=10 (аппарат/день)). Общее число аппаратов, находящихся в эксплуатации у населения очень велико, а выходят они из строя независимо друг от друга. Поэтому имеются основания считать поток заявок пуассоновским. Пусть все мастера имеют одинаковую квалификацию и в среднем могут отремонтировать 2,5 аппарата в день каждый (µ=2,5 (аппарат/день)). Определить показатели качества обслуживания в данном ателье.

Вариант №11

Требуется оценить работу АТС, которая имеет 5 линий связи (n = 5). Если все 5 линий связи заняты, то абонент выбывает из системы. Предполагаем, что поток простейший с интенсивностью λ=2 (вызов/мин.). Продолжительность разговоров распределена экспоненциально, причем t_обсл=1минута. Определить показатели эффективности системы.

СОДЕРЖАНИЕ ОТЧЕТА

1) Цель работы;

2) постановка задачи;

3) решение задачи в соответствии с выбранным вариантом;

4) выводы по выполнению работы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Что такое теория массового обслуживания?

2) Что включает в себя понятие система массового обслуживания?

3) Какие существуют виды систем массового обслуживания?

4) Что относится к основным характеристикам и показателям эффективности систем массового обслуживания?

5) Укажите основные свойства (характеристики) входящего потока требований?

6) Перечислите основные особенности и характеристики систем массового обслуживания с ожиданием?

7) Каковы основные характеристики СМО с отказами?

8) Приведите примеры различных видов СМО?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Афанасьев М.Ю. Исследование операций в экономике: модели, задачи, решения. / М.Ю. Афанасьев, Б.П. Суворов.- М.:ИНФРА, 2003.-444с.

2. Вентцель Е.С. Исследование операций. Задачи, приниципы, методология./ Е.С. Вентцель.-М.: Высшая школа, 2001.-208с.

3. Зайченко Ю.П. Исследование операций./ Ю.П. Зайченко.- К.: Вища школа, 1975.-320с.

4. Конюховский П.В. Математические методы исследования операций. / П.В. Конюховский.- СПб.: Питер, 2001.-192с.

5. Кремер Н.Ш., Путко Б.А. Исследование операций в экономике./ Н.Ш. Кремер, Б.А. Бутко, И.М. Тришин.- М.:Банки и биржи, ЮНИТИ, 1997.-407с.

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: