 |
Миноры и алгебраические дополнения определителей.
|
|
|
|
ОПРЕДЕЛИТЕЛИ ВТОРОГО ПОРЯДКА И ИХ СВОЙСТВА.
Определителем второго порядка называется квадратная таблица из четырёх элементов
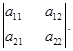(1)
Для элемента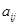 
номер строки - 
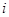, номер столбца – j. Элементами определителя могут могут быть числа, функции, векторы и т.д.
По определению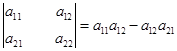 
(2)
Например:
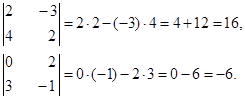
Рассмотрим простейшие свойства определителей второго порядка.
- Определитель не изменяется, если по строки заменить столбцами и наоборот, т.е.
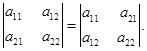Справедливость этого равенства следует из определения (2). Такая перестановка элементов определителя называется транспонированием. Из этого свойства следует справедливость всех рассмотренных ниже свойств как для элементов сток, так и для элементов столбцов.
- При перестановке двух столбцов (или сток) определитель меняет только знак.
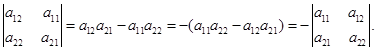
- Определитель с двумя одинаковыми столбцами (или строками) равен нулю.
.
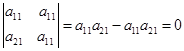4. Если все элементы какого-либо столбца (строки) равны нулю, то определитель равен нулю. 
- Если все элементы какого-либо столбца (строки) умножить на одно и тоже число, то определитель умножится на это число.
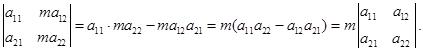
Это свойство выражает правило умножения определителя на число. Свойство 5 может быть сформулировано и следующим образом: или все элементы какого-либо столбца (строки) имеют общий множитель, то его можно вынести за знак определителя.
Например: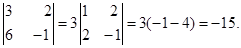 
- Определитель, у которого элементы двух столбцов (строк) соответственно пропорциональны равен нулю.
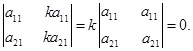
- Если каждый элемент какого-либо столбца (строки) определителя являются суммой двух слагаемых, то определитель равен сумме двух определителей, у одного из них элементами соответствующего столбца (строки) являются первые слагаемые, у второго – вторые. Остальные элементы у определителей – слагаемых те же, что у данного.
|
|
|
Предлагается доказать это свойство самостоятельно. Свойство 7 выражает правило сложения определителей.
- Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число.
.
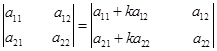Справедливость утверждения следует из свойств 6 и 7.
ОПРЕДЕЛИТЬЛЬ ТРЕТЬЕГО ПОРЯДКА И ИХ СВОЙСТВА
Определителем третьего прядка называются квадратная таблица из девяти элементов вида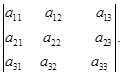 
Все обозначения индексов элементов и их расположение в таблице аналогичны там, которые были введены для определителей второго порядка. 
- элементы первого столбца (i = 1,2,3), 
- элементы первой строки (j = 1,2,3) и т.д. Элементы главной диагонали - 
элементы побочной диагонали -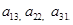 
По определению:
Это определение легко запомнить с помощью правила треугольников или правила Саррюса: со знаком плюс берутся произведения элементов, расположенных на главной диагонали, и произведения двух элементов, расположенных на параллелях к этой диагонали, на третьи множители из противоположных углов определителя; со знаком минус – произведения элементов, расположенных на побочной диагонали, и произведения двух элементов, расположенных на параллелях и этой диагонали, на третьи множители из противоположных углов определителя. Схема, по которой составляются произведения:
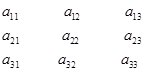
(со знаком плюс) (со знаком минус)
Такие же произведения можно составить по другой схеме:
К таблице из элементов определителя дописываем его первый и второй столбцы, произведения элементов, расположенных на главной диагонали и прямых, параллельных ей, берутся со знаком “плюс”, а произведения элементов, расположенных на побочных диагонали и прямых, параллельных ей, берутся со знаком “минус”.
Пример: 
|
|
|
МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ ОПРЕДЕЛИТЕЛЕЙ.
Минором любого элемента определителя называется, определитель второго
порядка, полученный вычеркиванием из данного определителя строки и столбца, содержащих этот элемент. Так минор для элемента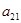 
для элемента 
:
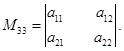
Алгебраическим дополнением любого элемента определителя называют минор этого элемента взятый с множителем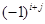 
, где i – номер строки элемента, j – номер столбца. Таким образом, алгебраическое дополнение элемента :
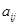Пример. Найти алгебраические дополнения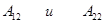 
для элементов определителя.
Теорема. Определитель равен сумме произведений элементов любого его столбца или строки на их алгебраические дополнения.
Другими словами, имеют место следующие равенства для определителя 
.
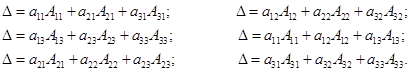
Доказательство этих равенств состоит из замены алгебраических дополнений их выражениями через элементы определителя, при этом получим выражение (3). Предлагается это выполнить самостоятельно. Замена определителя по одной из шести формул называется разложением определителя по элементам соответствующего столбца или строки. Эти разложения применяют для вычисления определителей.
Пример. Вычислить определитель, разложив его по элементам второго столбца.
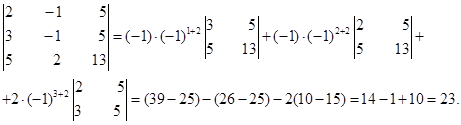
Используя теорему о разложении определителя третьего порядка по элементам строки или столбца, можно доказать справедливость свойств 1-8 для определителей третьего порядка. Предполагается проверить справедливость этого утверждения. Свойства определителей и теорема о разложении определителя по элементам столбца или строки позволяют упростить вычисления определителей.
Пример. Вычислить определитель.
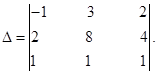
Вычислим общий множитель «2» элементов второй строки, а затем такой же общий множитель элементов третьего столбца.
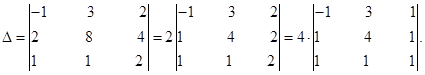
Прибавим элементы первой строки к соответствующим элементам второй строки, затем третьей строки.
Разложим определитель по элементам первого столбца:
Полезным является следующее утверждение: сумма произведений элементов какого-либо столбца (или строки) на алгебраические дополнения элементов какого-либо другого столбца (или строки) равна нулю, т.е. имеют место равенства:
Каждое из этих равенств представляет собой разложение определителя по элементам столбца (или строки), у которого одинаковы элементы столбцов (или строк).
|
|
|
|
|
|
