 |
Матрицы и операции над ними.
|
|
|
|
Матрицей из 
элементов 
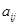называют прямоугольную таблицу вида:
Элементами матрицы могут быть числа, функции, векторы и т.д. Обозначения индексов элементов аналогичны тем, которые были введены для определителей.
Если m = 1, то получается матрица – строка:
если n = 1, то получается матрица – столбец:
Матрицы у которых число строк равно числу столбцов, называются квадратными. Среди квадратных матриц выделяют диагональные матрицы – матрицы, у которых все элементы, кроме расположенных на главной диагонали, равны нулю:
Если в такой матрице все элемента главной диагонали равны единице, то матрица называется единичной.
Матрица, все элементы которой равны 0, называются нулевой. Матрицы А и В называются равными, если они одинаковой размерности (равные числа строк и равные числа столбцов) и все соответственные элементы между собой. Пусть 
Введем основные операции над матрицами.
- Сложение и вычитание матриц.
Эти операции определяются только для матриц одинаковых размеров. Суммой матриц А+В называется матрица С тех же размеров, что А и В, элементы которой равны сумме соответствующих элементов матриц А и В, т.е.
Аналогично определяется операция вычитания матриц:
Пример.
- Умножение матрицы на число.
Произведением матрицы А и числа 
называется матрица 
тех же размеров, что и матрица А, элементы которой равны произведениям элементов матрицы А на это число, т.е.
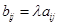
(при умножении матрицы на число следует все элементы матрицы умножить на это число).
Пример. 
Это определение может быть использовано для случая, когда все элементы матрицы имеют общий множитель, и этот общий множитель может быть вынесен за знак матрицы. Операции сложения матриц и умножения матрицы на число (линейные операции над матрицами) обладают свойствами:
|
|
|
где А,В,С – матрицы одинаковых размеров, 
- числа, 0 – нулевая матрица тех же размеров, что и А.
- Умножение матриц.
Произведением матриц 
называется матрица
элементы которой находятся по формуле
Из определения следует, что произведение матриц АВ.
Существует только в том случае, если первый множитель (матрица А) имеет столько столбцов, сколько строк имеет второй множитель (матрица В). Матрица – произведение (матрица С) имеет число строк, равное числу строк матрицы А, и число столбцов, равное числу столбцов матрицы В.
Из самого определения следует, что, если произведение АВ существует, то произведение ВА может не существовать.
Если АВ и ВА существуют, то в общем случае 
. Если все же такое равенство имеет место матрицы называются перестоновочными.
Поясним образование элементов матрицы С.
Из определения 
т.е. элемент 
(i- строка, j – столбец) равен сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В.
Произведение матриц 
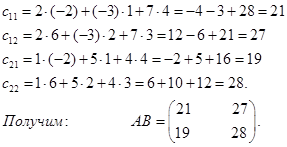
Для этих матриц существует и произведение ВА. Найдем его.
Д 
Получим: 
Это одновременно является и примером того, что 
Пример 2.
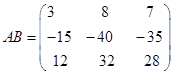
Для этих матриц существует произведение ВА.
Д 
Пример 3.
Свойство операции умножения матриц:
ОБРАТНАЯ МАТРИЦА.
Из элементов квадратной матрицы
составим определитель
Если 
то матрица называется невырожденной, если d (A) = 0, матрица А называется вырожденной.
Только для невырожденных матриц существует понятие обратной матрицы, которую обозначают 
.
Матрица называется обратной для квадратной невырожденной матрицы А, если
где Е – единичная матрица:
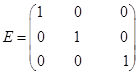
Для невырожденной матрицы существует только одна обратная матрица, которая находится по формуле:
|
|
|
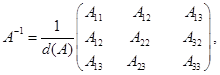
где 
- алгебраические дополнения элементов определителя d (A). Следует обратить внимание на то, что алгебраические дополнения элементов строк определителя служат элементами соответствующих столбцов матрицы.
Найдем, например, произведения 
:
При умножении матриц элементы главной диагонали представляли собой разложения определителя по элементам соответственно первого, второго, третьего столбцов, а все другие элементы равны нулю на основании свойства определителей.
Пример. Найти матрицу и проверить выполнение равенств 
, если
Вычислим определитель матрицы:
Матрица А невырожденная и имеет обратную матрицу. Найдём алгебраические дополнения элементов определителя.
Получим:
Найдем произведение 
|
|
|
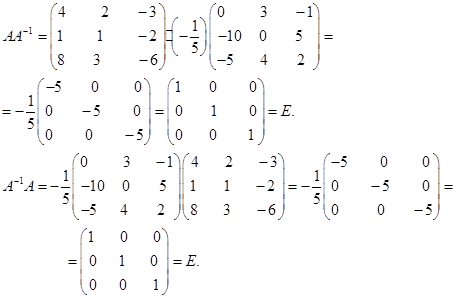
