 |
Производная сложной функции
|
|
|
|
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть функция  определена в некотором промежутке x. Дадим аргументу x некоторое приращение
определена в некотором промежутке x. Дадим аргументу x некоторое приращение  , не выходящие из промежутка х. Тогда при значении аргумента
, не выходящие из промежутка х. Тогда при значении аргумента  будем иметь
будем иметь  . Следовательно, приращение функции
. Следовательно, приращение функции  равно
равно
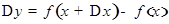
Предел отношения приращения функции  к приращению независимой переменной
к приращению независимой переменной  при стремлении
при стремлении  к 0, т.е.
к 0, т.е.
 ,
,
называется производной функции  по независимой переменной x.
по независимой переменной x.
Наряду с обозначением 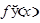 для производной употребляются и другие обозначения, например
для производной употребляются и другие обозначения, например
 .
.
Конкретное значение производной при  обозначается
обозначается  или
или 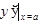 .Действие нахождения производной от функции
.Действие нахождения производной от функции  называется дифференцированием этой функции.
называется дифференцированием этой функции.
Пользуясь введённым понятием производной о скорости движения точки можно сказать следующее:
Скорость 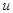 есть производная от производного пути S по переменной t.
есть производная от производного пути S по переменной t.
Геометрический смысл производной.
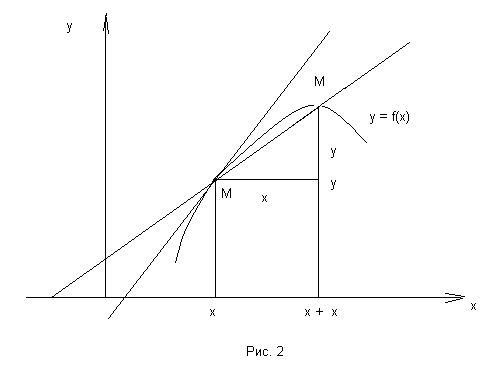
Рассмотрим функцию  и соответствующую ей кривую в прямоугольной системе координат. Значениям аргумента x и функции
и соответствующую ей кривую в прямоугольной системе координат. Значениям аргумента x и функции  на кривой соответствует точка
на кривой соответствует точка  . Дадим аргументу x приращение
. Дадим аргументу x приращение  . Новому значению аргумента
. Новому значению аргумента  соответствует значение функции
соответствует значение функции  . Соответствующей ему точкой кривой будет точка
. Соответствующей ему точкой кривой будет точка  . Проведём секущую
. Проведём секущую  и обозначим через
и обозначим через  угол, образованной секущей с положительным направлением оси Ox. Из рисунка видно, что
угол, образованной секущей с положительным направлением оси Ox. Из рисунка видно, что
 .
.
При  , точка
, точка  будет перемещаться вдоль кривой к точке
будет перемещаться вдоль кривой к точке  . Секущая
. Секущая  будет поворачиваться вокруг точки
будет поворачиваться вокруг точки  и угол
и угол  будет меняться с изменением
будет меняться с изменением  . При
. При  угол
угол  стремится к некоторому пределу
стремится к некоторому пределу  , а прямая, проходящая через
, а прямая, проходящая через  и составляющая угол
и составляющая угол  с положительным направлением, оси абсцисс, является касательной. Её егловой коэффициент
с положительным направлением, оси абсцисс, является касательной. Её егловой коэффициент
 .
.
Таким образом значение производной  в точке
в точке 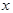 равна тангенсу угла наклона касательной проведённой, к графику функции в данной точке.
равна тангенсу угла наклона касательной проведённой, к графику функции в данной точке.
|
|
|
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ
Определение. Если функция  имеет производную в точке
имеет производную в точке  , т.е. исли существует
, т.е. исли существует
 ,
,
то при хначении  функция дифференцируема или имеет производную.
функция дифференцируема или имеет производную.
Если функция дифференцируема в каждой точке некоторого отрезка [a, b] или интервала (a, b), то говоря, что функция дифференцируема на отрезке [a, b] или в интервале (a, b).
Теорема. Если функция  дифференцируема в некоторой точке
дифференцируема в некоторой точке  , то она в этой точке непрерывна.
, то она в этой точке непрерывна.
Доказательство. Если  то
то  , где
, где 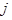 - величина бесконечно малая при
- величина бесконечно малая при  .
.
Тогда  . Отсюда следует, что
. Отсюда следует, что 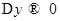 при
при  , а это значит, что функция
, а это значит, что функция  непрерывна в точке
непрерывна в точке  .
.
Таким образом в точках разрава функция не может иметь производной. Обратное утверждение неверно, т.е. из того, что в какой-нибудь точке  функция
функция  непрерывна, не следует, что в этой точке она дифференцируема.
непрерывна, не следует, что в этой точке она дифференцируема.
Производные основных элементарных функций

 где
где 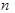 - натуральное число.
- натуральное число.
Дадим x приращение  , тогда новое значение
, тогда новое значение  будет
будет
 .
.
Пользуясь формулой бинома Ньютона, имеем

или
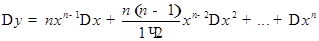
и

Так как при  все слогаемые кроме первого, стремятся к нулю, то
все слогаемые кроме первого, стремятся к нулю, то
 .
.
 Дадим
Дадим 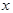 приращение
приращение  . Тогда
. Тогда  и
и
 ,
,
 Степенная функция:
Степенная функция:  , где
, где  - любое вещественное число.
- любое вещественное число.
Имеем 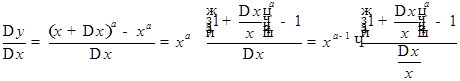 .
.
 .
.
Таким образом 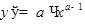 .
.
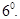 Показательная функция:
Показательная функция:
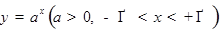
Здесь 
Перейдя к пределу, получим
 .
.
В частности, если  , то
, то  .
.
 Логагифмическая функция:
Логагифмическая функция:

В этом случае

Переходя к пределу, найдём
 .
.
В частности при  имеем
имеем  .
.
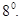 Тригонометрические функции.
Тригонометрические функции.
Пусть  тогда
тогда
 .
.
Пользуясь непрерывностью функции  и изветным пределом
и изветным пределом 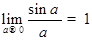 , получим
, получим

Т.о. 
Аналогично найдём производную функции  .
.
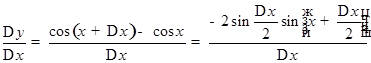
 .
.
В случае  имеем
имеем


Т.е.  .
.
Аналогично, если  , то
, то 
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть задана сложная функция  , т.е. такая, что её можно представить в следующем виде:
, т.е. такая, что её можно представить в следующем виде:  или
или  . В выражении
. В выражении  переменную и называют промежуточным аргументом. Правило дифференцирования сложной функции сложной функции можно сформулировать в виде теоремы:
переменную и называют промежуточным аргументом. Правило дифференцирования сложной функции сложной функции можно сформулировать в виде теоремы:
|
|
|
Пусть  имеет в некоторой точке
имеет в некоторой точке  производную
производную  , а qфункция
, а qфункция  имеет в соответствующей точке
имеет в соответствующей точке  производную
производную  . Тогда сложная функция
. Тогда сложная функция  в точке
в точке 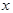 также будет иметь производную, равную произведению производных функций
также будет иметь производную, равную произведению производных функций  и
и  :
:  , или короче
, или короче 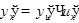 .
.
Доказательство. Дадим переменной 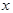 произвольное приращение
произвольное приращение  , которому соответствует приращение
, которому соответствует приращение 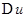 , а приращение
, а приращение 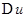 соответствует приращение
соответствует приращение  . Причём при
. Причём при  будет
будет  и
и 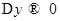 .
.
По условию теоремы  , а поэтому, пользуясь определение предела, можем записать (при
, а поэтому, пользуясь определение предела, можем записать (при 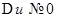 ):
):  , или короче
, или короче 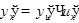 .
.
Доказательство. Дадим переменной x произвольное приращение  , которому соответствует приращение
, которому соответствует приращение 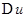 , а приращение
, а приращение 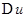 соответствует приращению
соответствует приращению  . Причем при
. Причем при  будет
будет  и
и 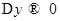 .
.
По условию теоремы  , а поэтому, пользуясь определением предела, можем записать (при
, а поэтому, пользуясь определением предела, можем записать (при 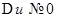 ):
):
 , (1)
, (1)
где  при
при  .
.
Перепишем равенство (1) в виде
 (2)
(2)
Это равенство справедливо и при  при произвольном
при произвольном  . Разделив его почленно на
. Разделив его почленно на  , получим
, получим
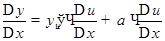 .
.
При  к нулю будет стремится и
к нулю будет стремится и 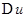
 , а также зависящие от
, а также зависящие от 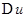 величина
величина  . Следовательно, существует предел
. Следовательно, существует предел
 , который и представляет собою искомую производную
, который и представляет собою искомую производную  .
.
Примеры. 1) Пусть  , иначе говоря,
, иначе говоря,  , где
, где  . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции 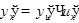 будем иметь
будем иметь  при
при  . Таким образом
. Таким образом  .
.
2) 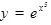 , т.е.
, т.е.  , где
, где  ;
;
 .
.
3)  т.е.
т.е.  , где
, где 
 .
.
4) 
5) 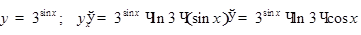 .
.
6)  ; в этом случае
; в этом случае
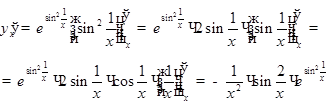
|
|
|


