 |
Производная обратной функции
|
|
|
|
Пусть дана возрастающая или убывающая функция  , т. е. между переменными
, т. е. между переменными 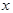 и
и  устанавливается взаимно однозначное соответствие. Рассматривая эти значения
устанавливается взаимно однозначное соответствие. Рассматривая эти значения  как значения аргумента, а
как значения аргумента, а 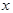 как значения функции, получим
как значения функции, получим 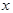 как функцию от
как функцию от  :
:
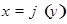 .
.
Эта функция называется обратной для функции  . Очевидно, что и функция
. Очевидно, что и функция  является обратной для функции
является обратной для функции 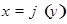 .
.
Теорема. Если для функции  существует обратная функция
существует обратная функция 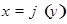 , которая рассмаириваемой точке
, которая рассмаириваемой точке  имеет производную
имеет производную  , отличную от нуля, то в соответствующей точке
, отличную от нуля, то в соответствующей точке 
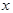 функция
функция  имеет производную
имеет производную 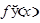 равную
равную  т.е. справедлива формула
т.е. справедлива формула
 . (*)
. (*)
Доказательство. Дифференцируя обу части равенства 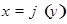 по
по 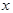 , считая
, считая  функцией от
функцией от 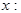
 Откуда
Откуда  . Учитывая, что
. Учитывая, что 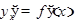 , получаем формулу (*), которую можно записать в виде
, получаем формулу (*), которую можно записать в виде
 (**)
(**)
Легко выяснить ее геометрический смысл. Мы знаем что, производная  есть тангенс угла
есть тангенс угла  , образованного касательной к графику функции
, образованного касательной к графику функции

 с осью
с осью 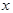 . Но обратная функция
. Но обратная функция 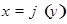 имеет тот же график, лишь независимая переменная для нее откладывается по оси
имеет тот же график, лишь независимая переменная для нее откладывается по оси  . Поэтому производная
. Поэтому производная  равна тангенсу угла
равна тангенсу угла  , составленной той же касательной с осью
, составленной той же касательной с осью  . Таким образом выведенная формула сводится к известному соотношению
. Таким образом выведенная формула сводится к известному соотношению  , связывающему тангенсы двух углов
, связывающему тангенсы двух углов  и
и  , сумма которых равна
, сумма которых равна  .
.
 Обратные тригонометрические функции
Обратные тригонометрические функции
Рассмотрим функцию  , причём
, причём 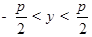 . Она является обратной для функции
. Она является обратной для функции  , имеющей положительную производную
, имеющей положительную производную  . В таком случае существует также производная
. В таком случае существует также производная  и равна по нашей формуле
и равна по нашей формуле
 ;
;
корень берём со знаком «плюс», так как  .
.
Значения 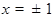 мы исключили, ибо для соответствующих значений
мы исключили, ибо для соответствующих значений  производная
производная 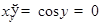 .
.
Функция  служит обратной для функции
служит обратной для функции  .
.
По нашей формуле  . Аналогично можно получить:
. Аналогично можно получить:
для 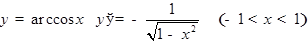 ,
,
для  .
.
Примеры. 1) 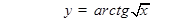

2) 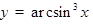 .
.

3) 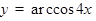
 .
.
4)  .
.
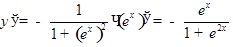 .
.
ТАБЛИЦА ПРОИЗВОДНЫХ
|
|
|














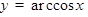

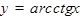
| 

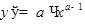






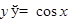
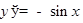



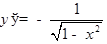

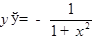
|
ПРОСТЕЙШИЕ ПРАВИЛА ВЫЧИСЛЕНИЯ
ПРОИЗВОДНЫХ
 Постоянный множитель можно вынести за знак производной
Постоянный множитель можно вынести за знак производной  где
где 
Докозательство: Дадим независимой переменной  приращение
приращение  , тогда функция получит приращение
, тогда функция получит приращение  равное
равное
 .
.
Разделим обе части равенства на  и перейдем к пределу при
и перейдем к пределу при  .
.
 т.е.
т.е.  .
.
Пример. 

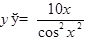
 Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций.
Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций.
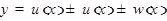

Доказательство. Дадим переменной 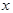 приращение
приращение  . Для значения аргумента
. Для значения аргумента  имеем
имеем  , где
, где  - приращения функций
- приращения функций  соответствующие приращению
соответствующие приращению  . Отсюда
. Отсюда  .
.
Разделим на 
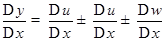 . Следовательно,
. Следовательно, 
Или окончательно

Пример.  ,
,
 .
.
 производная двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй функции, т.е.
производная двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй функции, т.е.
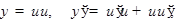 где
где 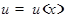 и
и 
Доказательство. Приращение аргумента  соответствуют приращения
соответствуют приращения 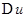 ,
, 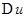 и
и  . При этом
. При этом
 и
и
 ,
,
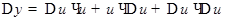 ,
,

Так как при  и
и  , то
, то  , т.е. существует производная
, т.е. существует производная 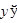 и равна
и равна

Если  , при чём
, при чём  и
и  существуют, то
существуют, то

Примеры: а) 

б) 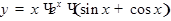

 . Производная дроби (частного от деления двух функций) равна дроби, числитель которой равен разности производной между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, а знаменатель есть квадрат знаменателя данной дроби.
. Производная дроби (частного от деления двух функций) равна дроби, числитель которой равен разности производной между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, а знаменатель есть квадрат знаменателя данной дроби.
Поизводная дроби (частного от деления двух функций) равна производной числителя, умноженной на знаменатель, минус числитель, умноженный на производную знаменателя, и деленное все на квадрат знаменателя, т.е.
если 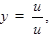 то
то 
Доказательство. Если 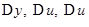 суть приращения функций
суть приращения функций 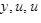 соответствующие приращению
соответствующие приращению  аргумента
аргумента 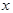 , то
, то 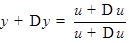 ,
,
|
|
|
 ,
,
 .
.
Устремляя  к нулю (причем одновремеено и
к нулю (причем одновремеено и  ), получим,
), получим,

Примеры: а) 

б) 

|
|
|


