Современные научные исследования требуют обязательных расчётов уровня статистической значимости результатов.

Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P>0,95. Общий смысл критерия останется тем же.

2. 2-й уровень значимости: р ≤ 0,01.

Уровень значимости – это допустимая ошибка в нашем утверждении, в нашем выводе.

33. t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

t -статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии.

Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:

где М₁ - средняя арифметическая первой сравниваемой совокупности (группы), М₂ - средняя арифметическая второй сравниваемой совокупности (группы), m₁ - средняя ошибка первой средней арифметической, m₂ - средняя ошибка второй средней арифметической.

Критерий Фишера применяется для проверки равенства дисперсий двух выборок. Его относят к критериям рассеяния.

При проверке гипотезы положения (гипотезы о равенстве средних значений в двух выборках) с использованием критерия Стьюдента имеет смысл предварительно проверить гипотезу о равенстве дисперсий. Если она верна, то для сравнения средних можно воспользоваться более мощным критерием.

В регрессионном анализе критерий Фишера позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется в шаговой регрессии для проверки целесообразности включения или исключения независимых переменных (признаков) в регрессионную модель.

В дисперсионном анализе критерий Фишера позволяет оценивать значимость факторов и их взаимодействия.

Критерий Фишера основан на дополнительных предположениях о независимости и нормальности выборок данных. Перед его применением рекомендуется выполнить проверку нормальности.

Заданы две выборки .

Обозначим через и дисперсии выборок и , и — выборочные оценки дисперсий и :

;

,

где

— выборочные средние выборок и .

Критерий хи-квадрат — любая статистическая проверка гипотезы, в которой выборочное распределение критерия имеет распределение хи-квадрат при условии верности нулевой гипотезы. Считается, что критерий хи-квадрат — это критерий, который асимптотически верен, то есть, выборочное распределение можно сделать как угодно близким к распределению хи-квадрат путём увеличения размера выборки.
34. Критерий - Пирсона

Критерий применяют для проверки гипотезы о том, что случайная величина подчинена закону распределения , по выборке , . По выборке строят функцию распределения случайной величины .

Для этого область изменения значений случайной величины разбивают на интервалы , , и определяют частоту попадания значений случайной величины в каждый интервал , а также теоретическую вероятность 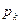. Затем вычисляют значение случайной величины

,

которая распределена по закону с степенями свободы.

При помощи таблиц находят границу критической области при уровне значимости 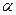. Если , то принимается решение о справедливости основной гипотезы, в противном случае принимается решение о справедливости альтернативы.

35.стр 187