Математические модели случайных сигнлов

Классификация сигналов

 

Сигналы можно классифицировать по различным признакам:

1. Непрерывные ( аналоговые) - сигналы, которые описываются непрерывными функциями времени, т.е. принимают непрерывное множество значений на интервале определения. Дискретные - описываются дискретными функциями времени т.е. принимают конечное множество значений на интервале определения.

Детерминированные - сигналы, которые описываются детерминированными функциями времени, т.е. значения которых определены в любой момент времени. Случайные - описываются случайными функциями времени, т.е. значения которых в любой момент времени является случайной величиной. Случайные процессы (СП) можно классифицировать на стационарные, нестационарные, эргодические и неэргодические, а так же, гауссовы, марковские и т.д.

3. Периодические - сигналы, значения которых повторяются через интервал, равный периоду

х (t) = х (t+nT), где n = 1,2,...,¥; T - период.

 

4. Kаузальные - сигналы, имеющие начало во времени.

5. Финитные - сигналы конечной длительности и равные нулю вне интервала определения.

6. Когерентные - сигналы, совпадающие во всех точках определения.

7. Ортогональные - сигналы противоположные когерентным.

 

Характеристики сигналов

 

1. Длительность сигнала ( время передачи) Т_с - интервал времени, в течении которого существует сигнал.

2. Ширина спектра F_c - диапазон частот, в пределах которых сосредоточена основная мощность сигнала.

3. База сигнала - произведение ширины спектра сигнала на его длительность.

4. Динамический диапазон D_c - логарифм отношения максимальной мощности сигнала - P_max к минимальной - P_{min (}минимально-различи-мая на уровне помех):

 

D_c = log (P_max/P_min).

 

В выражениях, где может быть использованы логарифмы с любым основанием, основание логарифма не указывается.

Как правило, основание логарифма определяет единицу измерения (например: десятичный - [Бел], натуральный - [Непер]).

5. Объем сигнала определяется соотношением V_c = T_cF_cD_{c .}

6. Энергетические характеристики: мгновенная мощность - P (t); средняя мощность - P_ср и энергия - E. Эти характеристики определяются соотношениями:

P (t) = x² (t); ;  (1)

 

где T = t_max- t_min.

Математические модели случайных сигнлов

 

Детерминированное, т.е. заранее известное сообщение, не содержит информации, т.к получателю заранее известно, каким будет переда-ваемый сигнал. Поэтому сигналы носят статистический характер [11].

Случайный (стохастический, вероятностный) процесс - процесс, который описывается случайными функциями времени.

Случайный процесс Х (t) может быть представлен ансамблем неслучайных функций времени x_i (t), называемых реализациями или выборками (см. рис.1).

 

 

Рис.1. Реализации случайного процесса X (t)

 

Полной статистической характеристикой случайного процесса является n - мерная функция распределения: F_n (x₁, x₂,..., x_n; t₁, t₂,..., t_n), или плотность вероятности f_n (x₁, x₂,..., x_n; t₁, t₂,..., t_n).

Использование многомерных законов связанно с определенными трудностями, поэтому часто ограничиваются использованием одномерных законов f₁ (x, t), характеризующих статистические характеристики случайного процесса в отдельные моменты времени, называемые сечениями случайного процесса или двумерных f₂ (x₁, x₂; t₁, t₂), характеризующих не только статистические характеристики отдельных сечений, но и их статистическую взаимосвязь.

Законы распределения являются исчерпывающими характеристиками случайного процесса, но случайные процессы могут быть достаточно полно охарактеризованы и с помощью, так называемых, числовых характеристик (начальных, центральных и смешанных моментов). При этом наиболее часто используются следующие характеристики: математическое ожидание (начальный момент первого порядка)

 

; (2)

 

средний квадрат (начальный момент второго порядка)

 

; (3)

 

дисперсия (центральный момент второго порядка)

 

; (4)

 

корреляционная функция, которая равна корреляционному моменту соответствующих сечений случайного процесса

 

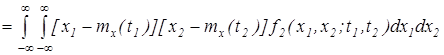. (5)

 

При этом справедливо следующее соотношение:

 

 (6)

Стационарные процессы - процессы, в которых числовые характеристики не зависят от времени.

Эргодические процессы - процесс, в которых результаты усреднения и по множеству совпадают.

Гауссовы процессы - процессы с нормальным законом распределения:

 

 (7)

 

Этот закон играет исключительно важную роль в теории передачи сигналов, т.к большинство помех являются нормальными.

В соответствии с центральной предельной теоремой большинство случайных процессов являются гауссовыми.

М арковский процесс - случайный процесс, у которых вероятность каждого последующего значения определяется только одним предыдущим значением.

12	Поделиться:

Воспользуйтесь поиском по сайту: